Предел последовательности

Заданы вещ-ые числа, пронум-е опр-ым образом: т.е. х₁ - имеет номер 1, х₂ - номер 2 и т.д. это наз. числовой послед-ю: х₁, х₂,…,х_n, …

Числа сост-е послед-ть, наз-т ее членами. Числ послед-ть считается заданной, если указано правило или закон, с пом-ю которого по номеру места в послед-ти всегда м/о назвать число, стоящее на этом месте.

О: послед-ть – это ф-ия натур-го аргумента. a_n=f(n). a_n=1/n. Обл опр-я ф-и – мн-во натур-х чисел.

О: число А наз пределом числ послед-ти a_n при неогр-м возраст номера n (n®¥), если для произв-го сколь угодно малого полож-го числа действ-го e, найдется такое натур число N, что для всех номеров n>N знач-я соотв-х членов числ послед-ти удовл-т нерав-у: |a_n-A|<e;

.

Св-ва: 1. Если переменная имеет предел, то он ед-й. Перем-я не м иметь 2-х различн пред-в. Док-во: допустим противное. Пусть х_n имеет два предела: limx_n=a и limx_n=b, где a¹b. Для опред-ти a<b. Возьмем число r (a<r<b). Т.к. x_n®a, a<r, то по т. (если перем-я х_n имеет пределом а, и а меньше некот-го числа с, то знач-я этой перем-й, начиная с некот-го n, будут также меньше этого числа с) найдется такое натур N_a, что x_n<r для всех знач-й n>N_a. Т.к. x_n®b, b>r, то по т. (если переменная х_n имеет пределом а, и а больше некот-го числа b, то знач-я этой перем-й, начиная с некот-го n, будут также больше этого числа b) найдется натур-е число N_b, что x_n>r для всех значений n>N_b. Получили нерав-ва: x_n<r для n>N_a; x_n>r для n>N_b. Если же теперь взять за N наиб из чисел N_a и N_b, то очев, что для всех знач n>N выпол-ся одновр-но оба нерав-ва, что невозможно. Получили противоречие.

2. если имеем две переменные величины x_n и y_n, имеющие пределы а и b, причем x_n= y_n для всех n, то a=b. Справедл-ть этой т. вытекает из того, что x_n и y_n по существу обозначают одну перем-ю, а потому в силу единств-ти предела a=b.

3. если имеем 2 перем-е величины x_n и y_n, имеющие пределы а и b, причем x_n£ y_n для всех n, то a£b.

Пусть дано метрич-е прост-во Х с метрикой r(x,y) и послед-ть х_nÎX.

О: точка аÎХ наз-ся пределом послед-ти (х_n) ("e>0) ($N) ("n) (n>N =>r(x_n,a)<e), тогда запис-т

;

. Послед-ть х_n сходящ-ся в точке а.

О: т-ка а явл-ся предельной точкой множ-ва Е ó, когда $ послед-ть точек из Е х_n¹a, сходящ-ся к а.

О: послед-ть х_n точек метрич-го прост-ва Х наз-ся фундаментальной, если ("e>0) ($N) ("m,n) (m>N, n>N =>r(x_m,x_n)<e), т.е. r(x_m,x_n)®0 при m,n®¥ (по мере увеличения номеров послед-ти, расстояние м/у членами послед-ти уменьшается).

Т: если послед-ть х_n сходится, то она фундаментальна.

Фунд-ть есть необходимое условие сходимости.

О: метрическое пр-во Х наз-ся полным, если в нем каждая фунд-ая посл-ть сх-ся к точке пр-ва Х.

Т (критерий Коши): для того, чтобы посл-ть х_n точек полного метр-го прост-тва Х сходилось, необх. и дост-но, чтобы она была фунд-ной.

Геом-я интерпретация: в любую сколь угодно малую e - окрестность а попадет ¥ много членов данной посл-ти (так для "e), вне этой окр-ти, всегда будет конечное мн-во членов.

;

Док-во: "e>0 … N=?;

; ; ;

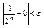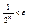Т: если послед-ть имеет конечный предел, то она ограничена (обратное не верно пр: х_n=(-1)ⁿ).

Д-во: пусть х_n®a. По опр предела это означает, ("e>0) ($N) ("n) (n>N - т.е. начиная с n₀=N+1) (|x_n-a|<e) или (a-e<x_n<a+e). Получили, что мн-во знач-й х_n, начиная с n₀=N+1, ограничена. Следовательно х_n - ограничена по т (если мн-во значений х_n начиная с некоторого значения n, ограничено, то х_n является огр-ой величиной).

Т: монот-о возраст-я (убыв-я) и огран-я сверху (снизу) послед-ть сх-я (имеет предел).

Утв: если посл-ть {a_n} имеет своим пределом число а, то выделенная из нее любым способом подпосл-ть {a_kn}также будет иметь своим пределом число а.

Т: из всякой огран-й посл-ти м-о выделить сход-юся подпосл-ть.

Т1: если посл-ти x_n и y_n имеют конечные пределы, то сумма и разность этих посл-тей также имеют конечные пределы, причем lim(x_n+y_n)=limx_n+limy_n. lim(x_n-y_n)=limx_n-limy_n. Др словами: предел алгеб-й суммы 2-х посл-тей, имеющих конечные пределы, равен алг-й сумме пределов этих посл-тей.

Т2: если посл-ти x_n и y_n имеют конечные пределы, то их произв-е также имеет предел, причем lim(x_n*y_n)=limx_n*limy_n.(произв-е пределов этих переменных).

Т3: если посл-ти x_n и y_n имеют конечные пределы, причем limy_n¹0, то их частное x_n/y_n имеет также предел, причем lim(x_n/y_n)=limx_n/limy_n.

Геом-й смысл:

Пр: lim 1/n=0, lim n!= ¥, lim (-1)ⁿ-не сущ., lim 2n-1/n+1=2.

,

Док-во:

, выполняется за счет выбора n.

Функц-ная послед-ть – члены – ф-и, определенные на некотором мн-ве. Если м-во фиксировано, то функц. ряд превр-ся в числовой ряд. Предел функц. посл-ти в общем случае является ф-й: lim f_n(x)=f(x). Напр, f_n(x)=x/(1+n²x⁵) сх-я к f(x)=0, т.к. для любого фиксир-го х (не ноль) знаменатель стремится к ¥ при n->¥. f_n(0)=0.