Любую строку расширенной матрицы системы можно умножить на некоторое число и прибавить к любой другой строке

Метод Гаусса (метод последовательного исключения пе –ременных) при использовании расширенной матрицы системы сводится к получению нулей ниже главной диагонали данной матрицы с помощью эквивалентных преобразований, чаще всего с помощью преобразования 4.

Если в результате элементарных преобразований в рас- ширенной матрице системы, до черты (т.е. в основной мат- рице) получается матрица треугольного вида, т.е. все элемен- ты ниже главной диагонали равны нулю, а диагональные эле- менты все ненулевые:

,

то рассматриваемая система совместная и определённая, т.е. имеет единственное решение.

Если после преобразований, в какой - либо строке матрицы получили до черты все нулевые элементы, а элемент, стоя -щий в той же строке после черты - ненулевой, например

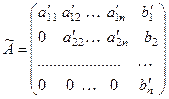
где 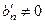, то рассматривая система несовместна, т.е. не имеет решений.

Если же после преобразования расширенной матрицы, пос- ле получения нулей ниже главной диагонали в нижней строке основной матрицы осталось больше одного ненулевого эле –мента, т.е. основная матрица имеет вид трапеции, например

,

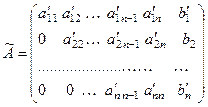то система имеет бесконечно много решений.

Рассмотрим пример решения системы методом Гаусса. Пусть дана система:

Составим расширенную матрицу этой системы:

˜

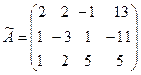Поменяем местами первую и третью строки матрицы:

˜ ˜

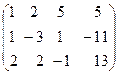С помощью первой строки полученной матрицы получим нули в первом столбце. Для этого первую строку умножим на (-1) и прибавим к второй строке, и её же умножим на (-2) и приба -вим к третьей строке, Получим новую матрицу

˜ ˜

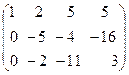Умножим третью строку на (-3) и прибавим к второй строке и эту же строку прибавим к первой строке, получим

˜ ˜

Вторую строку умножим на (2) и прибавим к третьей

˜ ˜ ˜

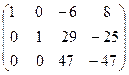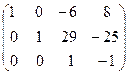Мы разделили последнюю строку на 47. После это третью строку умножим на (-29) и прибавим к второй строке и ту же строку умножим на (6) и прибавим к первой строке:

˜ .

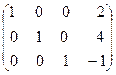Слева от черты получили единичную матрицу, тогда после черты получено решение данной системы. Таким образом, 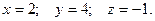Сделаем проверку:

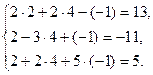
Получили тождественные равенства. Следовательно, в самом деле получено решение системы.

Рассмотрим ещё один пример:

Расширенная матрица этой системы имеет вид:

˜

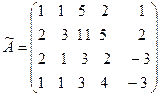Умножим первую строку на (-2) и прибавим к второй и тре -тьей строке, эту же строку умножим на (-1) и прибавим к четвёртой строке, получим:

˜ ˜

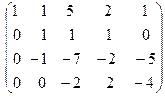Вторую строку умножим на (-1) и прибавим к первой строке и вторую строку просто прибавим к третьей строке:

˜ ˜

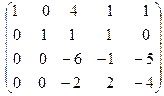Четвёртую строку разделим на (-2) и поменяем с третьей строкой:

˜ ˜

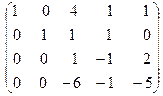После этого получим нули в третьем столбце, для чего тре- тью строку умножим на (-4) и прибавим к первой строке; ум -ножим на (-1) и прибавим к второй строке; умножим на (6) и прибавим к третьей строке. Получим:

˜ ˜ ˜

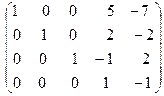Мы разделили последнюю строку на (-7). После этого можем получить нули в четвёртом столбце. Для этого последнюю строку прибавим к третьей строке; умножим на (-2) и приба- вим к второй строке и, умножив на (-5), прибавим к первой строке. В результате получается матрица:

˜ .

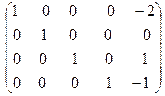Слева, до черты, получили единичную матрицу. Тогда после черты находится решение, т.е.

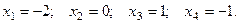
Подставив эти значения переменных в равенства системы, получим тождественные равенства.

Прежде чем перейти к рассмотрению систем произвольной размерности, вернёмся снова к понятию ранга матрицы, вве -дённому в § 3. Приведём утверждение, доказывать которое мы не будем.

Date: 2015-12-10; view: 420; Нарушение авторских прав