
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вектор. Сложение векторов. Умножение вектора на число. Векторное пространство
Вектором называется направленный отрезок, т.е. отрезок, у которого учитывается упорядоченность его концов (рис.7).

 ,
,  - обозначение вектора. Длиной вектора
- обозначение вектора. Длиной вектора  называют длину отрезка АВ, пишут │
называют длину отрезка АВ, пишут │ 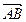 │= АВ или │
│= АВ или │ 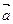 │= АВ.
│= АВ.
 Вектор называют нулевым, если его длина равна 0, т.е.
Вектор называют нулевым, если его длина равна 0, т.е. 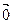 =
= 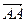 . Вектор называют единичным, если длина его равна единице. Для вектора
. Вектор называют единичным, если длина его равна единице. Для вектора  вектор
вектор  называют противоположным, пишут:
называют противоположным, пишут:  = -
= -  . Векторы
. Векторы  и
и  называются коллинеарными (обозначают
называются коллинеарными (обозначают  //
//  ), если прямые АВ и СD параллельны. Коллинеарные векторы могут быть сонаправленными:
), если прямые АВ и СD параллельны. Коллинеарные векторы могут быть сонаправленными: 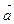

 или противоположно направленными:
или противоположно направленными: 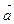
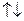
 .
.
 Сложение векторов: пусть даны векторы
Сложение векторов: пусть даны векторы 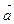 и
и 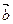 .
.
Отложим вектор 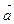 от некоторой точки А, т.е.
от некоторой точки А, т.е.  =
= 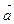 ; от точки В отложим вектор
; от точки В отложим вектор 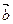 , т.е.
, т.е.  =
= 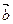 (рис.9). Тогда определен вектор
(рис.9). Тогда определен вектор  . Вектор
. Вектор  =
=  называется суммой векторов
называется суммой векторов 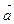 и
и 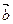 , т.е.
, т.е. 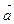 +
+ 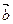 =
=  или
или 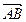 +
+  =
=  .
.
Таким образом, для любых трех точек А,В,С справедливо равенство (правило треугольника):
 +
+ 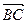 =
=  . (1)
. (1)
Используя правило треугольника, получаем:
 , (2)
, (2)
 . (3)
. (3)
Сложение векторов коммутативно (рис.10): 
 +
+ 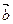 =
= 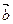 +
+ 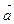 . (4)
. (4)
Рис.10
Очевидно, что вектор  в этом случае содержит диагональ параллелограмма (может быть, вырожденного), построенного на векторах
в этом случае содержит диагональ параллелограмма (может быть, вырожденного), построенного на векторах 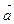 и
и 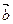 .
.
Сложение векторов ассоциативно (рис.11):
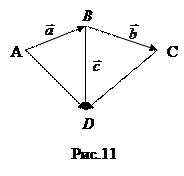
 . (5)
. (5)
Пусть  то
то  .
.
Тогда 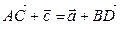 , откуда получаем равенство (5).
, откуда получаем равенство (5).
Таким образом, сумма трех векторов не зависит от порядка слагаемых.
Аналогично определяется сумма нескольких векторов. Так, например, при нахождении суммы четырех векторов  строится многоугольник, стороны которого определяют заданные векторы и результат сложения векторов. Это правило построения суммы нескольких векторов называется правилом многоугольника.
строится многоугольник, стороны которого определяют заданные векторы и результат сложения векторов. Это правило построения суммы нескольких векторов называется правилом многоугольника.
Векторы  называются компланарными, если существует плоскость, которой они параллельны.
называются компланарными, если существует плоскость, которой они параллельны.
Разностью двух векторов 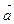 и
и 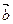 называется сумма вектора
называется сумма вектора  и вектора
и вектора  , противоположного вектору
, противоположного вектору 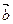 .
.
Произведением вектора 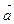 на действительное число λ
на действительное число λ
называется вектор 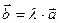 , удовлетворяющий условиям:
, удовлетворяющий условиям:
1)│ 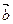 │=│
│=│ 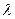 │∙│
│∙│ 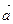 │,
│,
2) векторы 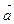 и
и 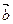 сонаправлены, если λ> 0, и противоположно направлены, если λ < 0.
сонаправлены, если λ> 0, и противоположно направлены, если λ < 0.
Произведение вектора на число обладает следующими свойствами:  (6)
(6)
 , (7)
, (7)
 , (8)
, (8)
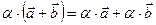 . (9)
. (9)
Используя определение произведения вектора 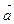 на действительное число λ, нетрудно обосновать, что: векторы
на действительное число λ, нетрудно обосновать, что: векторы  и
и 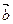 коллинеарны тогда и только тогда, когда существует такое действительное число λ, что
коллинеарны тогда и только тогда, когда существует такое действительное число λ, что 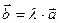 .
.
Свойства (2)-(9) называются аксиомами векторного пространства, а само множество векторов (направленных отрезков) V называют векторным пространством. Векторное пространство могут определять и другие множества, кроме множества направленных отрезков, например, множество всех матриц одной размерности.
Приведем аксиоматическое определение векторного пространства. Пусть дано непустое множество V, элементы которого будем называть векторами и обозначать  и т.д., и множество действительных чисел R, в которых определены сложение векторов (внутренний закон композиции) и умножение вектора на число (внешний закон композиции).
и т.д., и множество действительных чисел R, в которых определены сложение векторов (внутренний закон композиции) и умножение вектора на число (внешний закон композиции).
Тогда V называют векторным пространством над полем действительных чисел R, если введенные выше операции удовлетворяют следующим аксиомам векторного пространства. Для любых векторов  из V и для любых действительных чисел
из V и для любых действительных чисел  из R:
из R:
- Сложение векторов коммутативно:
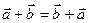 .
. - Сложение векторов ассоциативно:

- Существование нулевого вектора
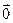 :
: 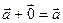
- Существование противоположного вектора
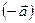 :
: 
- Умножение любого вектора
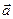 на 1 не изменяет вектор:
на 1 не изменяет вектор: 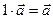
- Умножение вектора на число дистрибутивно относительно сложения векторов:

- Умножение вектора на число дистрибутивно относительно сложения чисел:
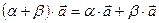
-

Важное значение в векторном пространстве имеет понятие линейной зависимости (независимости) векторов. Согласно определению §12, система векторов 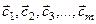 называется линейно зависимой, если существуют числа
называется линейно зависимой, если существуют числа  не равные нулю одновременно, что имеет место:
не равные нулю одновременно, что имеет место:  . (1)
. (1)
Система векторов 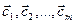 называется линейно независимой, если равенство (1) выполняется лишь тогда, когда все числа
называется линейно независимой, если равенство (1) выполняется лишь тогда, когда все числа 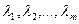 равны нулю. Свойства линейной зависимости системы векторов приведены в §12.
равны нулю. Свойства линейной зависимости системы векторов приведены в §12.
Понятие линейной зависимости (независимости) векторов позволяет ввести аксиомы размерности векторного пространства:
- Существует n линейно независимых векторов
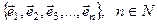 ,
,
- Любая система из n +1 вектора линейно зависима.
В силу этих аксиом определяется понятие базиса векторного пространства.
Базисом векторного пространства называется упорядоченная система n векторов 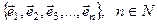 , удовлетворяющая условиям:
, удовлетворяющая условиям:
1)  - линейно независима,
- линейно независима,
2) всякий вектор 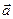 из V представим в виде линейной комбинации:
из V представим в виде линейной комбинации:  .
.
При этом коэффициенты  называются координатами вектора
называются координатами вектора 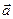 в базисе
в базисе  , пишут
, пишут  .
.
Число векторов базиса определяет размерность векторного пространства. Если базис состоит из n векторов, то V называют n -мерным векторным пространством и обозначают  .
.
Первоначально рассмотрим объекты трёхмерного пространства 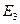 , и соответствующего ему трёхмерного векторного пространства
, и соответствующего ему трёхмерного векторного пространства  .
.
Пример. В базисе  заданы векторы
заданы векторы 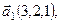
 . Проверить, что векторы
. Проверить, что векторы 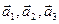 образуют новый базис
образуют новый базис  .
.
Решение: если векторы 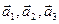 образуют базис, то они линейно независимы, т.е. должно выполняться условие
образуют базис, то они линейно независимы, т.е. должно выполняться условие
rang  =3, что очевидно, т.к матрица приводится с помощью элементарных преобразований к следующему виду:
=3, что очевидно, т.к матрица приводится с помощью элементарных преобразований к следующему виду:  .
.
Остается проверить, что для всякого вектора 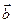 из
из  выполняется векторное равенство
выполняется векторное равенство 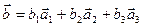 , что также очевидно, т.к. rang
, что также очевидно, т.к. rang  =3.
=3.
Date: 2015-12-10; view: 409; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |