
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод Гаусса. Системой m линейных (алгебраических) уравнений с n неизвестными называется система вида:
Системой m линейных (алгебраических) уравнений с n неизвестными называется система вида:
 (1)
(1)
где числа  (
( ; j =
; j =  , m,n – конечные натуральные числа)называются коэффициентами системы, bi - свободные члены.
, m,n – конечные натуральные числа)называются коэффициентами системы, bi - свободные члены.
Решением системы (1) называется упорядоченный набор чисел 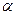 1,
1, 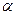 2, …,
2, …, 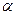 n, таких, что при подстановке вместо х1 числа
n, таких, что при подстановке вместо х1 числа 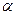 1, вместо х2 числа
1, вместо х2 числа 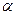 2 и т.д. все уравнения системы обратятся в тождества. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет (ни одного) решения.
2 и т.д. все уравнения системы обратятся в тождества. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет (ни одного) решения.
Система линейных уравнений может:
1) не иметь решения,
2) иметь более одного решения (система неопределенная),
3) иметь одно решение (система определенная).
Каждое решение неопределенной системы называется частным решением этой системы. Совокупность всех частных решений называется её общим решением.
Решить систему – это значит сначала выяснить, совместна она или несовместна. Если система совместна, то требуется найти её общее решение.
При решении системы линейных уравнений применяют к системе следующие элементарные преобразования:
-удаление уравнения вида  ,
,
-прибавление к какому-либо уравнению другого уравнения, умноженного на любое число.
Две системы называют равносильными, если каждое решение первой системы является решением второй системы, и обратно, каждое решение второй системы является решением первой. В записи равносильных систем используют знак « ».
».
Совершая элементарные преобразования, получаем систему, равносильную исходной.
Критерий совместности системы линейных уравнений выражает теорема Кронекера – Капелли:
Теорема. Система линейных уравнений (1) совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы системы, т.е. rang 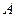 = rang
= rang  , где
, где

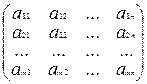 ;
; 

Для доказательства запишем систему линейных уравнений в матричном виде:  , где
, где
 -столбец свободных членов,
-столбец свободных членов,  - столбец неизвестных. Тогда система запишется в эквивалентной форме:
- столбец неизвестных. Тогда система запишется в эквивалентной форме:

 (2)
(2)
Обозначив столбцы  соответственно
соответственно  равенство (2) запишем в виде линейной комбинации столбцов
равенство (2) запишем в виде линейной комбинации столбцов
 .
.
Тогда, если система (1) (совместна) имеет решение  , то столбец
, то столбец 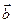 является линейной комбинацией столбцов матрицы А, т.е.
является линейной комбинацией столбцов матрицы А, т.е.  .
.
Обратно, если rang A = rang  , то
, то 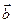 является линейной комбинацией системы
является линейной комбинацией системы  Значит, существует набор
Значит, существует набор  удовлетворяющий (2), что является решением системы (1), т.е. она совместна.
удовлетворяющий (2), что является решением системы (1), т.е. она совместна.
Метод Гаусса: процесс решения системы линейных уравнения по методу Гаусса состоит из двух этапов. На первом этапе с помощью элементарных преобразований приводят расширенную матрицу системы к треугольному виду. Второй этап заключается в решении системы линейных уравнений треугольного вида.
Рассмотрим этот метод на конкретном примере. Требуется решить систему линейных уравнений
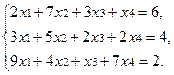
Очевидно, что элементарные преобразования системы соответствуют элементарным преобразованиям расширенной матрицы  системы:
системы:
 =
=  ~
~  ~
~  ~
~ 
Ранг расширенной матрицы  равен рангу основной матрицы, т.к. А =
равен рангу основной матрицы, т.к. А =  ~
~  ,
,
т.е. rang  = rang A =2. Получили следующую (треугольную) систему линейных уравнений:
= rang A =2. Получили следующую (треугольную) систему линейных уравнений:

Получим общее решение. Пусть  и
и  - свободные переменные, тогода
- свободные переменные, тогода 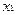 и
и  - главные. Выразим главные переменные через свободные:
- главные. Выразим главные переменные через свободные:

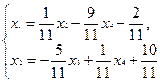 - общее решение.
- общее решение.
Если положить, например,  ,
,  , то найдем одно из частных решений системы
, то найдем одно из частных решений системы
 ;
;  ;
;  ;
;  .
.
Таким образом, для всякой совместной системы линейных уравнений:
1) если ранг расширенной матрицы меньше числа неизвестных, т.е. rang  =
= 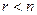 , то существует n-r свободных переменных и система имеет более одного решения.
, то существует n-r свободных переменных и система имеет более одного решения.
2) если ранг расширенной матрицы равен числу неизвестных, т.е.  , то система имеет единственное решение.
, то система имеет единственное решение.
Если в процессе решения получится противоречивое уравнение  , где
, где  , т.е. строка вида
, т.е. строка вида 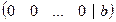 , то система несовместна.
, то система несовместна.
Date: 2015-12-10; view: 316; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |