
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод Симпсона
S4 = 0.08*(0.46065 + 4*(0.51845 + 0.65588 + 0.81691 + 0.99627) +2* (0.58383 + 0.73381 + 0.90458)+ 1.09153) =1.4357
Вычисление в MATLAB 6 по команде S = quad('(1+0.4*x.^2)./(2+ sqrt(0.5*x.^2+1.3))',1.2,3.12)
дает следующий результат S = 1.4357. Этот метод наиболее точный.
Тестовые задания для самопроверки усвоения темы.
- dy / dx = (y2 – y1) / h – это выражение для вычисления производной с помощью центральной разности?
- dy / dx = (-3 y0 +4 y1 + y2) /2 h - это выражение для вычисления производной с помощью интерполяционного полинома Лагранжа в точке y2?
- По заданной табличной функции вычислить значение производной в заданной точке.
-
 - это формула численного интегрирования Симпсона?
- это формула численного интегрирования Симпсона? - Зависит ли точность численного интегрирования от метода аппроксимации функции?
- Зависит ли точность численного интегрирования от шага табличной функции?
- Для заданной функции вычислить определенный интеграл.
РАЗДЕЛ 2
Методы и алгоритмы многочленного и немногочленного приближения
С помощью законов природы зависимости
величин, выражающих отдельные факторы
изучаемого явления, формулируются в виде
уравнений, как правило, дифференциальных.
ак. Александр Андреевич Самарский, 1919
Тема 2.3 Системы линейных дифференциальных уравнений и их решение на ЭВМ
§ 2.3.1 Основные понятия и определения
Специалистам по автоматизации технологических процессов часто приходится проводить процедуру анализа динамики системы (анализ переходных процессов). Для этого нужно уметь численно решать системы обыкновенных дифференциальных уравнений (ОДУ), которые являются базовым математическим описанием систем на макроуровне. Такие уравнения содержат одну или несколько производных от искомой функции и могут быть представлены в виде:
F(x, y, y¢,…,y(n)) = 0, где x независимая переменная.
Дифференциальное уравнение n порядка может быть сведено к n уравнениям первого порядкам путем введения новых переменных.
y = y1, y¢= y2, y¢¢= y¢2= y3, y¢¢¢ = y¢¢3 = y4, …, y(n-1) = yn-1 получится система ОДУ первого порядка:
y¢1= y2
y¢2= y3
y¢3 = y4
……….
y¢ n-1 = f(x, y1, y2, y3, …, yn-1)
Пример: Исходное уравнение - 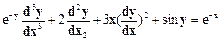
Введем новые переменные: y = y1, y¢= y2, y¢¢= y¢2= y3 и запишем систему из трех уравнений:

Как известно из математического анализа решением ОДУ является всякая функция, которая после подстановки в исходное уравнение превращает его в тождество.
Для уравнения первого порядка общее решение зависит от одной произвольной постоянной.
Y = j(x, C)
Частное решение зависит от определенного значения произвольной постоянной. Если произвольная постоянная принимает значение C = C0, (начальные условия – н.у.), то можно получить частное решение.
y = j(x, C0)
В зависимости от способа задания дополнительных условий для получения частного решения ОДУ существует два различных типа задач: задача Коши и краевая задача. В задаче Коши задаются только начальные условия (условия на левой границе решения).
При решении краевой задачи задаются начальные и граничные условия (условия на правой границе решения).
§ 2.3.2 Алгоритмы решения задачи Коши
К настоящему времени разработано много методов численного решения ОДУ для этой задачи. Все они сводятся к представлению производных конечными разностями, что приводит к разностному уравнению сеточной (табличной) функции в виде:
yi+1 = F(xi, hi, yi+1, yi, …,yi-k+1), i=1,2,…,k при н.у. y(0) = Y0 и шаге сетки hi.
Если в правой части этого уравнения отсутствует yi+1, т.е. значение yi+1 в левой части
yi+1 = F(xi, hi, yi, …,yi-k+1)
вычисляется по k предыдущим, то метод называют явным k – шаговым: k = 1 –одношаговый, yi+1 = F(xi, hi, yi); k = 2 – yi+1 = F(xi, hi,, yi, yi-1) двух шаговый и т.д.
Если в правую часть входит искомое значение yi+1, то метод называют неявным и решение этого уравнения ищется итерационно. Таким образом возможно использование четырех методов: явный одношаговый, явный многошаговый, неявный одношаговый, неявный многошаговый.
Рассмотрим алгоритм одношагового, явного метода, предложенного Эйлером.
Если решить ОДУ относительно производной,y¢= f(x,y), то, заменив правой разностью производную y¢= (yi+1-, yi)/h, получим следующее разностное уравнение
yi+1= yi + h´f(xi, yi)
В принципе шаг h может быть постоянным или меняться на каждом следующем значении xi. В инженерных задачах по автоматизации в качестве независимой переменной вместо xi используют время – t.
Пример 1. Решить ОДУ первого порядка по формуле Эйлера.
 , при начальных условиях. t = 0 y = y0, где
, при начальных условиях. t = 0 y = y0, где 
T - постоянная времени звена первого порядка. Воздействие на входе звена - x. В общем случае оно зависит от времени х(t).
Решим это уравнение относительно производной  .
.  1/T(kx - y)
1/T(kx - y)
При x= const разностное уравнение запишется в следующей форме.
 = yi +hf(t,y) = yi +Δy
= yi +hf(t,y) = yi +Δy
т. е. каждое новое значение представляет собой сумму предыдущего значения и его приращения на каждом шаге, равное произведению шага на значение функции от f(t,y).
Решение можно представить табличной функцией, например, для T= 5 c, k = 2, x = 1, h = 0.1, t = 0, y0 = 0
В качестве независимой переменной здесь вместо xi будет ti, а f(xi, yi)= f(ti, yi) правая часть ОДУ, разрешенного относительно производной, а х входное воздействие.
Таблица 1
| i | |||||
| ti | 0.1 | 0.2 | 0.3 | 0.4 | |
| yi | 0.04 | 0.0792 | 0.1176 | 0.1552 | |
| yi точ | 0.03960 | 0.0784 | 0.1165 | 0.154 |
y1=y0+h· (k·x/T-1/T·y0)= 0 + 0.1·(2·1/5 – 1/5·0) = 0.04
y2=y1+h·k·x/T-1/T·y1)= 0.04 + 0.1·(2·1/5 – 1/5·0.04) = 0.0792
y3=y2+h· (k·x/T-1/T·y2)= 0.0792 + 0.1·(2·1/5 – 1/5·0.0792) = 0.1176
y4=y3+h· (k·x/T-1/T·y3)= 0.1176 + 0.1·(2·1/5 – 1/5·0.1176) = 0.1552 и т.д.
Абсолютная погрешность при i=1 Δy1 = ׀ 0.04-0.0396 ׀ = 0.0004, δ = 0.0004/0.0396 = 0.0101 = 1.01%,
При i=2 Δy2= ׀ 0.0792-0.0784 ׀ = 0.0008, δ = 0.0008/0.0784 = 0.0102 = 1.02%,
Существуют и другие явные одношаговые методы. Наиболее распространенным из них является Рунге-Кутта.
 = yi +Δy, где
= yi +Δy, где
k0 = hf(xi, yi); k1 = hf(xi +h/2, yi +k0/2);
k2 = hf(xi +h/2, yi +k1/2); k3 = hf(xi +h, yi +k2);
Здесь xi –это значение независимой переменной.
Этот метод требует на каждом шаге четырехкратного вычисления правой части уравнения.
Пример 2. Решим уравнение примера 1 методом Рунге-Кутта, для k = 1, а результаты сведем в таблицу.
При решении примера независимая переменная t, а x постоянное входное воздействие.
| i | ||||
| ti | 0.2 | 0.3 | 0.4 | |
| yi | 0.03960265 | 0.078421121 | 0.116470932 | |
| к0 | 0.04 | 0.039207946 | 0.038431577 | 0.037670581 |
| к1 | 0.0396 | 0.038815867 | 0.038047261 | 0.037293875 |
| к2 | 0.039604 | 0.038819788 | 0.038051104 | 0.037297642 |
| к3 | 0.3920792 | 0.038431551 | 0.037670555 | 0.036924628 |
| Δy | 0.0396026 | 0.038818468 | 0.038049811 | 0.037296374 |
| yi +1 | 0.03960265 | 0.078421121 | 0.116470932 | 0.153767307 |
| yi точ | 0.03960265 | 0.078421121 | 0.116470932 | 0.153767307 |
Поскольку
k0= 1/Th(kx-y0) = 0.1·1/5(2-0)=0.04;
k1= 1/Th(kx-y0 +k0/2)= 0.1·1/5(2-0.02)= 0.0396;
k2= 1/Th(kx-y0 +k1/2)= 0.1·1/5(2-0.0198)= 0.039604;
k3= 1/Th(kx-y0 +k2)= 0.1·1/5(2-0.039604)= 0.3920792;
y1= y0 +1/6·(k0+2k1 +2k2 +k3)= 0 +1/6·(0.04+ 2·0.0396 +2·0.039604 + 0.3920792) = 0.0396026
Это уравнение имеет аналитическое решение: y =xk(1- e-ti /T).
Для t1=0.1 y= 1· 2· (1-exp(-0.1/5))= 0.03960265 (оставлено 7 значащих цифр).
Метод Рунге Кутта точнее и не дает ошибки при таком количестве значащих цифр в этой точке.
Об остальных методах можно узнать из рекомендованной литературы.
Точное и числовое решение на ЭВМ естественно отличается друг от друга на величину полной ошибки ei на каждом шаге интегрирования.
Полная ошибка интегрирования на i-шаге зависит от следующих основных составляющих:
1. Ошибки аппроксимации (усеченная методическая ошибка) ei1, которая связана с заменой производных конечно-разностными отношениями (процедура алгебраизации). Это неустранимая ошибка.
2.Ошибки вычислений округления ei2, связанной с ошибками округления чисел в ЭВМ и заменой неарифметических операций и функций арифметическими при вычислении yi. Для современных ЭВМ ей можно пренебречь.
3. Ошибки накопления (распространения) ei3, равной полной ошибке по ei на предыдущем шаге.
Таким образом, ei = ei1 +ei2 +ei3 и растет при увеличении числа шагов вычислений. При вычислении на ЭВМ с использованием пакетов прикладных программ допустимая ошибка, как правило, указывается в исходных данных.
В примере 1 для первой точки возникает ошибка первого типа, так как накопления пока нет. Во второй точке ошибка имеет уже две составляющие
§ 2.3.3 Алгоритм решения краевой задачи ОДУ.
Если кроме начальных условий задаются граничные условия, то задача называется краевой. Краевые задачи существуют для уравнений порядка выше первого.
Например, для линейного дифференциального уравнения второго порядка
y" + p(x)y' + g(x)y = f(x)
Решение y(x) должно удовлетворять условию на отрезке [a, b] y(a) = A, y(b) = B (3.43)
Граничные условия могут быть заданы и в общем, виде
a1y(a) + b1y'(a) = A
a2 (b) + b2 y'(b) = B
Численные методы решения уравнения вида (3.42) делятся на две группы: сведение решения краевой задачи к последовательности решений задачи Коши и использование конечно-разностных методов.
Конечно-разностные методы решения краевой задачи сводят ее решение путем алгебраизации производных к решению системы алгебраических уравнений относительно значений искомой функции на заданном множестве точек. Алгоритм решения рассмотрим на конкретном примере.
Пусть требуется решить уравнение
y" + x·y' - 0.5y/x = 1
на интервале [2, 2.3] при заданных краевых условиях
y(2) + 2y'(2) = 1
y(2.3) = 2.15
Выберем шаг h = 0.1, тогда множество точек решения будет x0 = 2,0; x1 = 2,1; x2 = 2,2; x3 = 2,3;
Точки x1 и x2 лежат внутри интервала, на котором ищется решение, x0 x3 точки граничных условий.
Запишем, конечно- разностное представление граничных условий и уравнения для всех точек.

В первом уравнении первая производная представлена конечно-разностным выражением по трех точеченой схеме для точки x0 = 2,0 (численное дифференцирование с помощью полинома Лагранжа).
Во второй и третьей точках решения - x1; x2 в конечных разностях записывается выражение ОДУ. Для представления первых производных использованы центральные разности, а для второй производной вторые разности. После преобразований получим

Подставив значение y3 в третье уравнение, получим систему из трех уравнений

Система представляет собой СЛАУ, которая решается известными методами. Его решение дает следующий результат.
y0= 2.235, y1= 2.185, y2= 2.158, y3= 2.15
Для решения краевой задачи используют и другие методы, описанные в рекомендованной литературе и в частности метод "стрельбы".
Тестовые задания для проверки усвоения темы.
1. Дифференциальное уравнение T22 y" + T1y' +y = kx представить в виде системы из двух ОДУ первого порядка.
2. yi+1 = yi + 1/6(k0 + 2k1 +2k3 + k4) – это выражение для численного решения ОДУ методом Эйлера?
3. Решить уравнение 1.52 y" + 6y' +y = 2x на отрезке [0 5] y(0) = 0 c шагом h = 0.5 методом Эйлера.
4. Какие задачи встречаются при решении ОДУ?
5. Существует ли краевая задача решения ОДУ для уравнения, содержащего производную третьего порядка?
6. Решить краевую задачу. y" + 2x2y' +y = x 2y(0.5) - y' (0.5) = 1; y(0.8) =3; h= 0.1.
7. a1y(a) + b1 y'(a) = A
a2 (b) + b2 y'(b) = B
Это форма задания начальных условий при решении краевой задачи ОДУ?
РАЗДЕЛ 2
Методы и алгоритмы многочленного и немногочленного приближения
Тема 2.4 Дифференциальные уравнения в частных производных и их численное решение на ЭВМ.
§ 2.4.1. Классификация дифференциальных уравнений в частных производных
В практике инженера по автоматизации для решения некоторых задач теплообмена в технологических объектах управления приходится использовать дифференциальные уравнения в частных производных (ДУЧП).
Чаще всего используют ДУЧП, которое описывает изменение состояния системы в пространстве одной координаты и по времени в виде общего уравнения:
 , (1)
, (1)
где Q – параметр (температура, давление или другая физическая величина)
ДУЧП классифицируют по трем признакам: математический вид уравнения, физический смысл и автор, впервые исследовавший уравнение, которые представлены в таблице 1.
Таблица 1
| Математический вид уравнения Гиперболическое Параболическое Эллиптическое Первого порядка | Физический смысл Волновое Теплопроводности (диффузии) Напряжение в веществе (прочности) Переноса субстанции (вещества) | Автор Даламбер Фурье (Пуассон) Лапласа |
Математическую основу уравнения определяет соотношение коэффициентов.
Если a = b = c = f = 0; d ¹ 0, e ¹ 0, то получаем уравнение первого порядка в частных производных.
 - уравнение переноса (2)
- уравнение переноса (2)
Если D = b - ac > 0, то вид уравнения – гиперболический ( нестационарная задача)
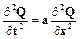 (3)
(3)
При D = 0, параболическое уравнение
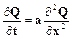 , где а > 0 (4)
, где а > 0 (4)
и если D > 0, то эллиптическое уравнение (стационарная задача)
 , (5)
, (5)
где в качестве второй переменной здесь является пространственная координата y, а производная по времени равна нулю.
Точное решение ДУЧП удается получить лишь для немногих частных случаев. В настоящее время для решения ДУЧП с помощью ЭВМ наиболее широкое распространение получил численный метод сеток. Его идея принадлежит Эйлеру.
§ 2.4.2 Метод сеток и алгоритмы его реализации
Сущность метода сеток состоит в аппроксимации искомой непрерывной функции совокупностью приближенных значений, рассчитанных в некоторых точках области - узлах. Совокупность узлов, соединенных определенным образом, образуют сетку. Сетка по сути дела является дискретной моделью области определения искомой функции. Дифференциальное уравнение заменяется конечно-разностным уравнением, при этом производные искомой функции в выбранных узлах заменяются разностями.
Применение метода сеток позволяет заменить дифференциальное уравнение системой нелинейных алгебраических уравнений для функции дискретных аргументов (сеточной функции), определенных в узлах сетки.
Начальные и краевые условия заменяются разностными начальными и краевыми условиями для сеточной функции. Полученная система решается, и таким образом определяются значения искомой функции в узлах сетки, т.е. численное решение задачи.
В общем случае алгоритм метода сеток состоит из трех этапов.
- Построение сетки в заданной области (дискретизация задачи).
- Аппроксимация ДУЧП разностным уравнением и получение системы алгебраических уравнений относительно узловых значений.
- Решение полученной системы уравнений.
Существует два принципиально отличных метода сеток для численного решения ДУЧП: метод конечных элементов (МКЭ) и метод конечных разностей (МКР).
Первый чаще используется при исследовании моделей, описывающих прочностные свойства систем. Рассмотрим подробнее метод конечных разностей
Реализацию МКР начинают с построения сетки в заданной области. Для одномерной области отрезок L разбивается на N частей. Расстояние между двумя соседними узлами называется шагом сетки hi = xi - xi-1 при i = 1,2,3,...,N.
Для регулярной сетки - hi шаг - величина постоянная.
Для двухмерной функции используют различные области изменения функции. На плоскости часто применяют квадратные, прямоугольные, треугольные, шестиугольные сетки для представления области изменения функции. Для прямоугольной сетки, образованной системой прямых, xi= x0 + ih, и yj = y0 + jl, (i, j = 0, ± 1, ± 2, …). Постоянные положительные числа h, l называют шагом сетки по оси OX и OY соответственно. Если вместо координаты y используют время, то шаг обозначают - t. Узлы сетки, попавшие внутрь прямоугольника, называют внутренними (G). Точки пересечения прямых, образующих сетку, с границей области называют граничными узлами (Г). Узлы сетки нумеруются через индексы (x) - i; (y) - j. Вместо y часто используют координату времени t для нестационарных задач. Для трёхмерной области при нумерации узлов сетки используют индексы i, j, k.
Обозначим значение искомой функции Q(x,y) в узле (xi,yj) через Qi,j. В каждом внутреннем узле сетки заменим частные производные функции их конечными разностями, используя формулы численного дифференцирования.
 (6)
(6)
В граничных точках применяются менее точные разности.
 (7)
(7)
Вторые частные производные в каждом внутреннем узле заменяются разностями.
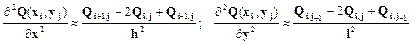 (8)
(8)
Множество узлов, значения сеточной функции в которых входят в выражение разностного уравнения в точке (i, j), называют шаблоном. Совокупность разностного уравнения и разностных краевых условий называется разностной схемой краевой задачи.
Любая схема должна удовлетворять условиям сходимости, точности и устойчивости, строгое доказательство которых проводится в учебниках по математике.
Сходимость заключается в том, что при стремлении шага сетки к нулю, погрешность приближённого решения краевой задачи также стремится к нулю, т.е. значение сеточной функции приближается к точным значениям исходной непрерывной функции в узлах сетки.
§ 2.4.3 Алгоритмы решения параболического уравнения
Наиболее характерной задачей в области автоматизации является оценка изменения температуры в среде при подводе или отводе к ней тепла. Математически этот процесс для одномерной задачи описывается параболическим уравнением.
 - коэффициент температуропроводности. (9)
- коэффициент температуропроводности. (9)
а l- теплопроводность, Вт/м. град;
c - теплоёмкость, Дж / кг. град;
r- плотность, кг/м3;
T - температура, 0C.
Физически искомая функция T(x, t) определяет температуру в любой точке полубесконечной пластины шириной 2L в момент времени t.
В области D = {x, t); 0 £ x £ L, 0 £ t £ T } заданы начальные условия (распределение температуры в начальный момент времени)
T(x, 0)= f(x), 0 £ x £ L
И краевые условия первого рода (тепловые режимы на концах пластины)
T(0, t)= j(t), T(2L, t)= y(t), 0 £ t £ T.
Функции f(x), j(t), y(t) предполагаются непрерывными.
В системе координат x0t построим прямоугольную сетку с шагом h по оси x и с шагом t по оси t и введем обозначения
xi = ih (I=0,1,2,3, …,n), h= L/n.
tj = j t (j= 0,1,2,3,…,m) t = T/m, T(xi, tj)= Tij
Заменим производные их конечно-разностным значением по 4-х точечному, явному шаблону и получим уравнение.
 , (10)
, (10)
Обозначив s = at / h2 (11)
го можно привести к виду

По этой формуле можно вычислить значение искомой функции T(xi, tj) в узлах j+1 временного слоя при t= tj+1, если известны её значения в узлах j слоя. При t = 0 значения функции получаются из начальных условий, а в левом и правом граничных узлах из граничных условий.
Для устойчивости вычислений при применении явного шаблона надо соблюсти дополнительное условие:
s £ 0.5
В частности, при s = 0.5 формула для вычислений существенно упрощается
Ti, j +1 = 0.5(Ti+1, j + Ti-1, j) (12)
При s = 1/6
Ti, j +1 = 1/6(Ti+1, j + 4Ti, j + Ti-1, j) (13)
Применение явного шаблона требует, чтобы шаг по времени выбирался после оценки шага по координате, как требуют условия устойчивости.
ПРИМЕР 1
Пластина толщиной 0.3 м, материал сталь с плотностью r = 7800 кг/м, нагретая до T0 = 700 0C, помещается в среду с T1 = 100 0C.
Теплофизические параметры с = 586,6 Дж/кг· 0С, λ= 45,4 Вт/м 0С, a = 9,92·10-6 м2 /с.
Для этого случая выберем упрощенные начальные и граничные условия:
T = T0 при t = 0
T = T0 при x = 0
T = T0 при x = 0.3 т.е. температура на левой и правой границе постоянна, а значит, решение будет симметричным и можно вычислить распределение температуры по времени на различных слоях только от левого края до центра.
. Расстояние до центра 0.15 м, поэтому разделим это расстояние на 6 частей (узлов), i = 1,2,3,4,5,6. h= 0.15/6 = 0.025 м
Шаг по времени по формуле будет τ = 31,5 c
Несколько шагов расчета можно представить в виде таблицы.
Таблица 3.1
| j | x=0 | x=0.025 | x=0.05 | x=0.075 | x=0.1 | x=0.125 | x=0.15 | x=0.175 | |
| t,c | T0 i=0 | Ti i=1 | Ti i=2 | Ti i=3 | Ti i=4 | Ti i=1 | Ti i=1 | Ti i=1 | |
| 31.5 | |||||||||
| 94.5 | 512.5 |
Значение в узле i=1, j=0 – (граничный узел) принимаем 0.5(100+700) = 400 0С
При s = 0.5 заполним таблицу, используя формулу
Расчёт можно вести до необходимого времени tк или до определенной температуры. Например, до тех пор, пока пластина не примет температуру среды.
В общем случае граничные условия могут быть более сложные.
Пример 2. Решить ДУЧП параболического типа  на отрезке [0; 0.6], h = 0.1, до t = 0.005 при граничных условиях:
на отрезке [0; 0.6], h = 0.1, до t = 0.005 при граничных условиях:
U(x,0) = x(x+2x)+1, u(0;t) = 1+0.5t, u(0.6;t)= 0.5, При s = 1/6
Параболическое уравнение решается методом сеток постепенным переходом от значений функции U(xi,ti) к значениям U(xi,tj+1), причем tj+1 = tj +k, где k = 0.01/6 = 0/0017
Вычисления производятся по формуле 0.0017 Ui,j+1 = (1/6)*(Ui+1,j +4* Ui,j + Ui - 1,j)
Таблица 3.2
| j | x=0 | x=0.1 | x=0.2 | x=0.3 | x=0.4 | x=0.5 | x=0.6 | |
| tj,c | Ui=0 | Ui i=1 | Ui i=2 | Ui i=3 | Ui i=4 | Ui i=5 | Ui i =6 | |
| 1.03 | 1.12 | 1.27 | 1.48 | 1.75 | 0.5 | |||
| 0.0017 | 1.09 | (1.12+4*1.03+1)/6=1.04 | 1.13 | 1.28 | 1.49 | 1.496 | 0.5 | |
| 0.0033 | 1.16 | 1.063 | 1.14 | 0.5 | ||||
| 0.0050 | 1,25 | 1.092 | 0.5 |
Краевые и начальные условия выделены жирным косым шрифтом. Остальные колонки заполняются по аналогии.
Аналогичная задача будет решаться в лабораторной работе.
Тестовые задания для проверки усвоения темы
1. Классифицировать.
Вид ДУЧП Название
1.  ; а) Гиперболическое 2.
; а) Гиперболическое 2.  ; б) Эллиптическое
; б) Эллиптическое
3.  ; в) Переноса 4.
; в) Переноса 4.  ; г) Параболическое
; г) Параболическое
2.  Это уравнение Пуассона?
Это уравнение Пуассона?
3. 
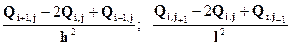
А) Б)
Где разностное уравнение для второй производной?
4.
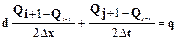 Это разностное уравнение для решения ДУЧП переноса?
Это разностное уравнение для решения ДУЧП переноса?
5. Нарисуйте прямоугольную сетку и обозначьте узлы для решения задачи Пуассона ЯВНЫМ четырех точечным шаблоном.
6. Запишите выражение для ДУЧП - переноса.
7. Запишите уравнение теплопроводности. Каким методом его решают численно? Какие шаблоны можно использовать?
8. По каким признакам классифицируют ДУЧП?
Раздел 3 Численное определение нулей и экстремумов функций
Посредством уравнений, теорем
Он уйму всяких разрешил проблем
англ. поэт Д. Чосер (1340 – 1400)
Тема 3.1. Методы и алгоритмы нахождение нулей функций
§ 3.1.1. Численное решение рациональных и трансцендентных уравнений
.
В практике инженеров по автоматизации встречаются задачи, когда необходимо решать одно или несколько нелинейных уравнений
Например, для расчета статической характеристики водо-водяного теплообменника надо решать систему из двух нелинейных уравнений.
 (3.1)
(3.1)
В качестве неизвестных в этих уравнениях t2 – конечная температура нагреваемой воды, T2 – конечная температура греющей среды.
Различают следующие типы нелинейных функций: алгебраические и трансцендентные. В свою очередь алгебраические делятся на виды: целые, рациональные и иррациональные, а трансцендентные на тригонометрические, логарифмические, показательные и др.
В частности многочлены вида a2 x2 +a1 x+a0 является целой алгебраической функцией, а уравнение состояния Дитеричи p(υ - b) = RT exp[-a/(RT υ)] трансцендентным.
В случае одного нелинейного уравнения с одним неизвестным решение сводится к нахождению корня уравнения вида
f(x)=0 (3.2).
Если x принимает значение корня, то выражение (3.2) превращается в тождество. Уравнение в общем случае может иметь несколько действительных и комплексных корней.
Если функция на интервале [a, b] имеет действительный корень, то при переходе аргумента через значение корня f(x) меняет знак (признак наличия действительного корня на интервале).
Методы решения нелинейных уравнений делятся на два типа: прямые и итерационные. Прямые методы (аналитические) позволяют записать выражение для получения значения корня. Известны формулы для решения квадратного и кубического многочлена, простейших тригонометрических, логарифмических и показательных уравнений.
Однако сложные математические описания реальных технических систем решать прямыми методами не удаётся. Для их решения используются итерационные методы (последовательных приближений).
В настоящее время существует несколько видов итерационных
методов, каждый из которых имеет своё наименование:
1. Перебора
2. Бисекции (деление отрезка пополам)
3. Хорд (пропорциональных частей)
4. Касательных (Ньютона-Рафсона)
5. Секущих (комбинированный)
6. Простой итерации.
Для понимания сути этих методов необходимо рассмотреть следующие понятия:
интервал изоляции корня - область изменения аргумента уравнения, где функция f(x)=0 меняет знак [a,b], т.е. f(a)·f(b)<0.
Выделение интервалов изоляции из всей области изменения аргумента в интервале от - ∞ до + ∞ будем называть процедурой определения корня.
Эту процедуру можно осуществить графически: вычислить несколько значений функции и построить график. Можно не строить график, а оценить только знаки функции на границе заданного интервала [a, b] и в ряде промежуточных точек.
Если существует непрерывная производная f'(x) и корни уравнения f'(x)=0 легко вычисляются, то процедура отделения корня упростится, так как для этого нужно проверить значения f(x) в точках корней её производной и граничных точках xн=a; xк=b.
Необходимую точность значения корня (погрешность решения) можно оценить по следующему соотношению:
|x* - e| £ f(x*)/m1, где
e - точность значения корня,
x* - приближённое значение корня,
m1 - наименьшее значение производной функции f¢(x)
на интервале изоляции корня [α, β]
α £ x* £ β
Чаще всего применяют соотношение, задаваясь допустимым интервалом изоляции корня
|x* - e| £ β -_ α или |xi+1 - xi| £ e
Это условие окончания итерационного процесса.
Иногда для условия окончания итерационного процесса применяется соотношение
|f(xi+1) - f(xi)| £ e,
но это не рекомендуется делать, так как могут быть большие погрешности.
Общий алгоритм итерационных методов может быть сформулирован следующим образом:
1. Задать значение аргумента x на концах начального интервала изоляции αн =a; βн =b и величину точности (погрешности) корня e.
2. Проверить, не достигается ли заданная погрешность на выбранном интервале |xi+1 - xi|. Если да, то закончить вычисления, иначе перейти к п.3.
3. Сформировать новый интервал изоляции корня. Вычислить соответствующие значения функции. Проверить условие смены знаков на концах нового интервала изоляции.
4. Перейти к пункту 2.
Методы поиска корня различаются по сути дела только процедурой выполнения пункта 3 алгоритма, т.е. способом сужения интервала изоляции для уточнения корня.
Наиболее простым и надежным является метод половинного деления (сужения) интервала. Его алгоритм можно представить следующим описанием.
- Ввести исходные данные xн=a; xк=b, e.
- Вычислить f(a).
- Вычислить xi = (a+b)/2 и f(xi).
- Если f(xi) ¹ 0, то перейти к пункту 5, иначе к пункту 7.
- Если xi – a ³ e, то перейти к пункту 6, иначе к пункту 7.
- Если f(a) × f(xi) > 0, положить a=xi, f(a) = f(xi), иначе положить b= xi. Перейти к пункту 3.
- Вывести значение x* и f(x*). Конец.
Date: 2015-10-22; view: 484; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |