
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример 3
f(x, y) = sin(2x-y) -1.2x - 0.4
j(x, y) = 0.8x2 +1.5y2 –1, в области параметров D={(x, y)½0.4 < x < 0.5;- 0.8 < y < - 0.7½
с точностью e = 0.01
¶f/¶x=2cos(2x-y) – 1.2; ¶f/¶y = -cos(2x-y)
¶j/¶x=1.6x; ¶j/¶y = 3y
За начальные приближения примем x0 = 0.4; y0= - 0.8
По формулам (3.4 – 3.5) D0 = 3.00147; Dx0 = - 0.2895; Dy0 = -0.1873, а по формуле (3.3)
вычисляем x1 = 0.4 – (- 0.2895/3.00147) = 0.4965; y0= - 0.8- (- 1873/3.00147)= - 0.7376.
Погрешность по формуле (3.6) равна 0.1149 т.е. больше допустимой погрешности и надо продолжить вычисления для x1, y1.повторная итерация дает x1= 0.4909; y1= -0.7331; погрешность равна 0.0071 т.е. вычисления можно прекратить.
§ 3.1.2. Нахождение действительных и комплексных корней многочленов
Очень часто модель системы описывается целым алгебраическим полиномом n степени
f(x) = anxn + an-1xn-1 +... + a1 x + a0 = 0
Применительно к таким уравнениям можно отметить ряд свойств, использование которых позволяет упростить решение задачи.
Теорема Гаусса. Уравнение n степени имеет всего n корней, среди которых могут быть как действительные, так и мнимые (комплексные), которые образуют комплексно-сопряжённые пары. Каждый корень считается столько раз, какова его кратность. Число c называется к – кратным корнем многочлена, если f(x) делится на (х-с)к, но не делится на (х-с)к+1, где с – корень многочлена f(c)= 0. Если k=1, то с - простой корень. Сумма кратности всех корней равна тепени многочлена.
Теорема Декарта. Число положительных действительных корней меньше или равно числу перемен знаков в последовательности коэффициентов an, an-1, a1,..., a0. Заменяя x на -x, таким же способом можно оценить число отрицательных корней.
Теорема Лагранжа. Верхняя граница положительных действительных корней определяется как
 , a0 > 0,
, a0 > 0,
где am – первый отрицательный коэффициент; B – наибольшая абсолютная величина отрицательного коэффициента.
Теорема Гюа. Если уравнение f(x) имеет действительные корни и действительные коэффициенты, то a2k > ak-1ak+1. В строго математическом смысле, найдя один корень х1 =с, можно разделить уравнение на (х-с), тем самым понизив его степень.
Для определения действительных корней многочлена применяют все вышеописанные итерационные методы. Комплексные корни можно найти методом Лина, Берстоу, которые подробно описаны в рекомендованной литературе.
Тестовые задания для проверки усвоения темы
1. Это алгебраическое уравнение?
(
2. Где целое алгебраическое уравнение?:
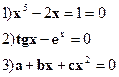
3. 1- Алгебраическое целое а) 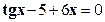
2 – Трансцендентное тригонометрическое б) 
3 Трансцендентное логарифмическое
4 -алгебраческое рациональное в) 
5 –алгебраическое иррациональное г) 
6 -трансцендентноепоказательное д) 
е) 
Классифицировать нелинейные уравнения.
4.
 Каким символом обозначен Якобиан в этих выражениях?
Каким символом обозначен Якобиан в этих выражениях?
5. Дано уравнение tg(0,55x + 0,1) + x2= 0
интервал изоляции [0,6 0,8].
Проверить, есть ли корень нак этом интервале.
6. 2x3 – y2 = 1x
xy3 – y = 4x Найти значение якобиана в точке x0 =1.2 y0 = 1.7 для этой системы уравнений.
3.2. Определение экстремальных значений нелинейных функций с помощью ЭВМ
В мире не происходит ничего,
в чем не был бы виден смысл
какого-либо максимума или минимума.
Леонард Эйлер (1707 – 1783)
§ 3.2.1. Основные понятия и определения
Нелинейные функции, представляющие математические модели технической системы, обычно характеризуют статические режимы системы (зависимость выходных параметров от входных). Например, коэффициент полезного действия топочного устройства зависит от коэффициента избытка воздуха не линейно.
Как правило, выходной параметр зависит от многих факторов - выходных параметров
y = f(x1, x2,..., xn)
Прежде всего, при моделировании, интересуются наилучшим (наибольшим, наименьшим) значением выходного параметра. Его поиск называют процедурой параметрической оптимизации. Оптимизировать можно самые разнообразные параметры технической системы (наилучший вариант конструкции, наилучшее распределение ресурсов и т.д.).
Величины x1, x2,..., xn называют проектными или управляемыми параметрами (их в процессе процедуры можно менять). Число параметров характеризует размерность задачи оптимизации.
Выбор оптимального решения или сравнение двух альтернативных решений проводится с учетом некоторых правил предпочтения на основе установленных критериев, скалярной меры качества.
В основе построения правил предпочтения лежит функция, определяемая проектными параметрами. Такую функцию называют целевой, а также функцией качества или критерием оптимальности.
В зависимости от содержательного смысла проектных параметров и выбранного смысла проектных параметров и выбранного способа их сочетания в целевой функции (ЦФ) качество технической системы будет тем выше, чем больше ее значение (максимизация) или чем
меньше ее значение (минимизация).
Выбор ЦФ носит субъективный характер и поэтому система может быть оптимальна только в смысле данного критерия.
Целевую функцию можно записать в виде:
F(x) = f(x1, x2,..., xn)
В качестве скалярной величины целевой функции может выступать физический параметр (температура), экономический показатель (прибыль, себестоимость) и др. ЦФ может быть представлена в виде таблицы, алгоритма. Целевых функций может быть несколько и тогда приходится выбирать определяющий критерий или производить их свертку.
Если в технической системе есть n проектных параметров, образующих вектор X = (x1, x2,..., xn). Целевая функция F(x) определена в некоторой области XO, то максимумом или минимумом F(x) называют ее значение F(X*). При этом для любой точки X Î Se(X), и достаточно малом e >0 (за исключением самой точки X*) выполняются неравенства:
F(x)-F(X*)< 0 или F(x)-F(X*)> 0 соответственно.
Здесь Se(X*) - e - окрестность точки X*, которая является множеством точек (векторов), которые находятся от этой точки на расстоянии не превышающих число e >0.
Se(X*) = {X | X - X | £ e}, где
|X – X* | - норма вектора X - X*, отождествляемая с расстоянием между точками X и X*.
Точку X* называют точкой локального экстремума. Глобальным экстремумом называют точку, в которой ЦФ имеет наибольшее (наименьшее) значение среди всех экстремумов области определения.
Функцию F(X) называют одно-экстремальной (унимодальной), если она имеет один экстремум и многоэкстремальной, если она имеет более одного максимума (минимума). Если изменить знак целевой функции на обратный, то задача оптимизации станет инверсной.
Если поиск экстремума F(X) производится в неограниченной области изменения вектора X, то экстремум называют безусловным (в противном случае - условным).
Чтобы точка X* была точкой локального безусловного экстремума функции F(X), которая является скалярной от векторного аргумента размерности n и дважды дифференцируема, необходимо, чтобы все её частные производные по элементам Xi вектора X в точке X* были равны 0, т.е.
¶F(X)/ ¶ Xi =0, X = X* при 1Î [1:n]
Это, так называемое, условие стационарности может быть записано в виде
ÑF(X*) = 0, где
 - градиент целевой функции в точке X*.
- градиент целевой функции в точке X*.
Градиентом функции F(X) в какой-либо точке Xn называют
n-мерный вектор, компоненты которого равны частным производным F(X), вычисленным в точке Xk по всем Xi. Характер экстремума F(X) в стационарной точке определяется
исследованием поведения F(X) в окрестности X*. Для этого формируется матрица вторых производных (матрица Гессе). Если она определена положительно, то в точке X функция F(X) имеет безусловный минимум. Если Ge F(X*) < 0, то это безусловный максимум. В остальных случаях это седловая точка.
Для n=1 и n=2 задача оптимизации имеет геометрическую интерпретацию. Одномерная оптимизация представляется кривой на плоскости, а двухмернаяповерхность в трёхмерном пространстве. Для двухмерной функции часто используют её представление в виде линий равного уровня, т.е. когда F(X) = C. Эти линии получаются пересечением поверхности F(X) плоскостью, параллельной осям координат X1, X2, что позволяет представлять характерные особенности ЦФ.
Если область определения ЦФ ограничена, то экстремум такой функции называют условным. Различают прямые и функциональные ограничения.
Прямые ограничения имеют вид
Xni < Xi < Xbi при i Î [1:n],
где Xni, Xbi минимально и максимально допустимые значения i-го проектного параметра. Например, многие проектные параметры не могут быть отрицательными (масса, геометрический размер и т.д.).
Функциональные ограничения представляют собой дополнительные взаимосвязи между проектными параметрами и параметрами, входящими в ЦФ. Они бывают двух видов:
1) тип равенств ψ(X) = 0;
2) тип неравенств ψ(X) > 0.
Прямые и функциональные ограничения формируют допустимую область поиска экстремума.
Постановка задачи оптимизации производится по следующему алгоритму:
1. Определяется вектор проектных параметров X.
2. Формируются ограничения на изменение X.
3. Составляется целевая функция.
Математическая формулировка задачи:
Безусловная оптимизация
min F(X)
X Î X0
Условная оптимизация
min F(X)
X Î XA
при ψ (X) = 0; ψ (X) > 0
Xni < Xi < Xbi, i Î [1:n]
Таким образом, можно различать два типа оптимизации: условная, безусловная и два вида: одномерная, многомерная.
Date: 2015-10-22; view: 449; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |