Метод интегрирования по частям неопределенных интегралов

Пусть и 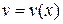дифференцируемые функции. Известно, что

.

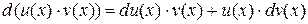Найдем неопределенные интегралы от функций, стоящих в левой и правой частях этого равенства, получим

.

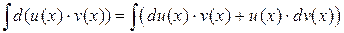Используем третье и пятое свойства интегралов, получим

.

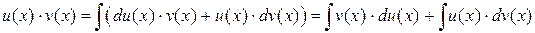Отсюда получается формула, которая называется формулой интегрирования по частям

.

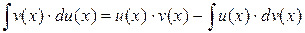Для лучшего запоминания запишем эту формулу в виде

.

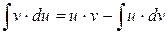Следовательно, если подынтегральное выражение можно разбить на 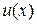и 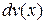так, что можно найт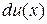и и 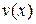, то исходный интеграл можно свести к нахождению другого интеграла, который возможно находится проще.

Имеются некоторые общие соображения о применении этого метода.

Так, если подынтегральная функция содержит произведение многочлена

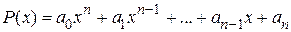
и одной из следующих функций:

,

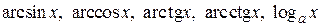то такие функции нужно принять за 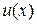, а многочлен включить в ().

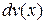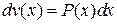Пример 4.21.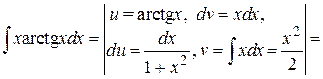

.

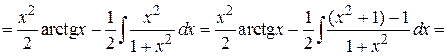
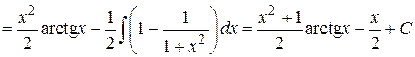Если же под интегралом имеется произведение многочлена 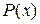и одной из функций:

,

то за 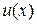нужно принять многочлен 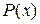, а за 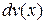все остальное подынтегральное выражение. При этом если степень многочлена больше единицы, то интегрирование по частям необходимо повторить столько раз, какова степень многочлена.

Пример 4.22.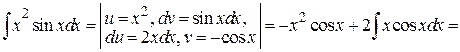

.

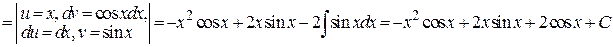Если под интегралом имеется произведение функци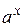и или 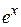на тригонометрическую функцию 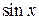или 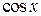, то в результате двукратного интегрирования по частям получается уравнение относительно исходного интеграла (интеграл возвращается к первоначальному виду). Такие интегралы называются «возвратными».

Пример 4.23.

.

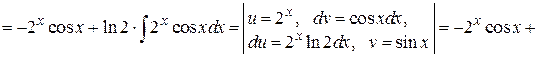
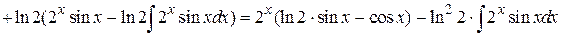Получили уравнение относительно исходного интеграла

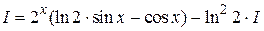Û .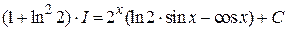

Отсюда .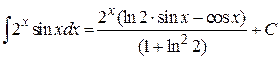

Пример 4.24.

.

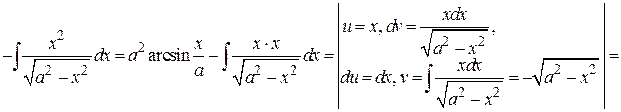
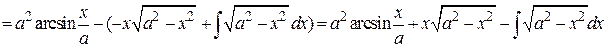Отсюда получаем

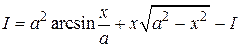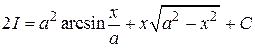Û Þ

.

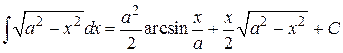Date: 2015-09-02; view: 427; Нарушение авторских прав