Приведение квадратичной формы к сумме квадратов

В этом параграфе указаны различные методы приведения квадратичной формы к сумме квадратов, т.е. будут указаны методы выбора такого базиса 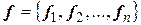в линейном пространстве , по отношению к которому квадратичная форма представляется в следующем каноническом виде:

, (4.12)

где 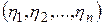– координаты в базисе .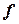

Коэффициенты 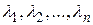в выражении (4.12) называются каноническими коэффициентами.

Подчеркнем, что мы рассматриваем квадратичные формы в произвольном вещественном линейном пространстве.

Настоящий параграф посвящен не только доказательству возможности приведения квадратичной формы к каноническому виду, но и описанию двух методов такого приведения, имеющих большую практическую ценность и широко встречающихся в приложениях.

Так как каждому преобразованию базиса отвечает невырожденное линейное преобразование координат, а невырожденному преобразованию координат – преобразование базиса, то вопрос о приведении формы к каноническому виду можно решать путем выбора соответствующего невырожденного преобразования координат.

1. Метод Лагранжа. Докажем следующую теорему.

Теорема 4.3 Любая квадратичная форма 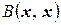, заданная в n-мерном линейном пространстве , с помощью невырожденного линейного преобразования координат может быть приведена к каноническому виду (4.12).

Доказательство. Проведем доказательство теоремы методом Лагранжа. Основная идея этого метода заключается в последовательном дополнении квадратного трехчлена по каждому аргументу до полного квадрата.

Будем считать, что 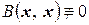и в данном базисе 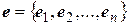имеет вид (4.11).

Убедимся, во-первых, что с помощью невырожденного преобразования координат форму 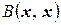можно преобразовать так, что коэффициент при квадрате первой координаты вектора будет отличен от нуля.

Если в данном базисе этот коэффициент отличен от нуля, то нужное невырожденное преобразование является тождественным.

В случае, если 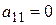, но отличен от нуля коэффициент при квадрате какой-либо другой координаты, то с помощью перенумерации базисных векторов можно добиться требуемого результата. Ясно, что перенумерация является невырожденным преобразованием.

Если же все коэффициенты при квадратах координат равны нулю, то нужное преобразование можно получить следующим способом. Пусть, например, . Рассмотрим следующее невырожденное преобразование координат:

, , , .

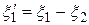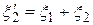После этого преобразования коэффициент при 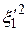будет равен 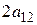и поэтому отличен от нуля.

Итак, будем считать, что в соотношении (4.11) 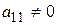. Выделим в выражении (4.11) ту группу слагаемых, которые содержат 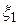. Получим

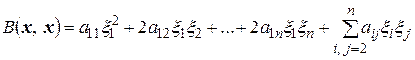. (4.13)

Преобразуем выделенную группу слагаемых следующим образом:

.

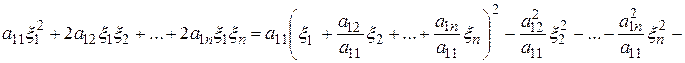
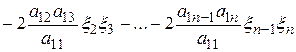Очевидно, выражение (4.13) можно теперь переписать так:

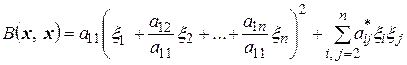, (4.14)

где 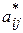– коэффициенты при 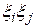, полученные после преобразования.

Рассмотрим следующее невырожденное преобразование координат:

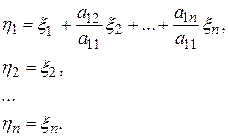
С помощью этого преобразования и представления (4.14) для получим

. (4.15)

Итак, если форма 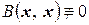, то с помощью невырожденного преобразования координат эту форму можно привести к виду (4.15).

Обратимся теперь к квадратичной форме 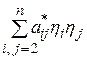. Если эта форма тождественно равна нулю, то вопрос о приведении 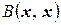к каноническому виду решен. Если же форма 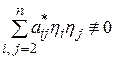, то мы можем повторить рассуждения, рассматривая преобразования координат 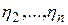, аналогичные описанным выше, и не меняя при этом координату 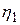. Очевидно, такого типа преобразования координат 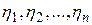будут невырожденными.

Ясно, что за конечное число шагов мы приведем квадратичную форму 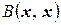к каноническому виду (4.12).

Отметим, что нужное преобразование исходных координат можно получить путем перемножения найденных в процессе рассуждений невырожденных преобразований. Теорема доказана.

Итак, первый способ решения основан на доказательстве теоремы Лагранжа.

Второй способ решения. Введем в рассмотрение следующую невырожденную матрицу

.

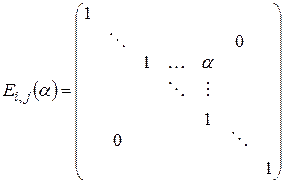Она получена из единичной матрицы заменой элемента, стоящего в i -й строке и j -ом столбце, на число . Если 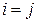, то необходимо, чтобы число 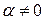. Для произвольной матрицы можно вычислить произведение . Непосредственной проверкой легко убедиться в том, что при 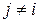это произведение можно получить из матрицы , если все столбцы, кроме j -го оставить без изменения, а к j -му столбцу прибавить i -й столбец, умноженный на . Если же 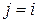, то произведение получается из матрицы умножением j -го столбца на .

Если же умножать матрицу на транспонированную матрицу 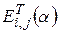слева, то есть вычислять 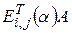, то это произведение получается из матрицы при 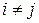прибавлением к j -ой строке i -й строки, умноженной на . Матрица 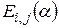является невырожденной, значит может выступать в роли матрицы перехода. Так как преобразование матрицы квадратичной формы происходит по формуле 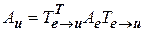, то матрица 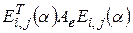будет матрицей квадратичной формы в некотором базисе. Выбирая последовательно подходящие матрицы 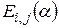, можно получить диагональную матрицу квадратичной формы, то есть привести ее к каноническому виду. Вместо умножения справа на матрицу 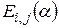будем выполнять элементарное преобразование столбцов: , а вместо умножения слева на ее транспонированную будем выполнять элементарное преобразование строк: . Обратим внимание на то, что в этих преобразованиях номера строк и столбцов одинаковы. Такое преобразование будем называть согласованным элементарным преобразованием строк и столбцов.

Замечание 1 Базис, в котором квадратичная форма имеет канонический вид, называется каноническим. Отметим, что канонический базис определен неоднозначно.

Замечание 2 Если форма 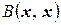приведена к каноническому виду (4.12), то, вообще говоря, не все канонические коэффициенты λ, отличны от нуля. Оставляя в (4.12) лишь отличные от нуля λ, и перенумеровывая их заново, получим следующее выражение для :

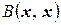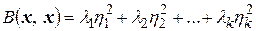. (4.16)

Ясно, что 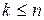. Так как ранг квадратичной формы по определению равен рангу ее матрицы в любом базисе, то из (4.16) и условия 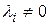при 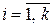вытекает, что ранг формы равен k. Таким образом, число отличных от нуля канонических коэффициентов равно рангу квадратичной формы.

Пример 3 Привести к каноническому виду квадратичную форму

.

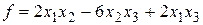Решение.

І способ. Сделаем замену переменных 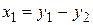, , 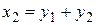. Тогда квадратичная форма преобразуется к виду

.

В соответствии со сказанным при доказательстве теоремы 3.1 сделаем новую замену переменных

, , ,

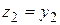получим

.

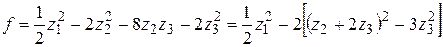После замены переменных , , 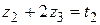квадратичная форма f будет приведена к каноническому виду

.

ІІ способ. Выполним согласованные элементарные преобразования строк и столбцов матрицы квадратичной формы и присоединенной единичной матрицы:

.

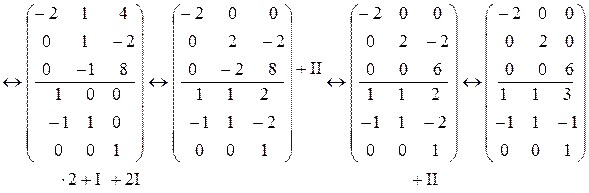Матрица третьего порядка, стоящая сверху, является диагональной. Значит, это матрица квадратичной формы, имеющей канонический вид. В соответствии с алгоритмом матрица третьего порядка, стоящая снизу – это искомая матрица перехода. Поэтому

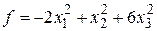
и

2. Метод Якоби. При некоторых дополнительных предположениях о квадратичной форме 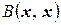можно указать явные формулы перехода от данного базиса 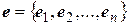к каноническому базису 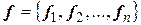и формулы для канонических коэффициентов .

Предварительно мы введем понятие треугольного преобразования базисных векторов.

Преобразование базисных векторов 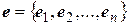называется треугольным, если оно имеет следующий вид:

(4.17)

Замечание. Так как определитель матрицы треугольного преобразования (4.17) отличен от нуля (равен 1), то векторы 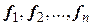образуют базис.

Введем в рассмотрение угловые миноры матрицы коэффициентов формы в базисе е, обозначив их символами , , …, :

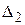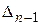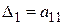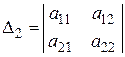, , …, . (4.18)

Справедливо следующее утверждение.

Теорема 4.4 (Якоби) Пусть миноры , , 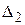…, 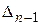матрицы 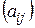квадратичной формы отличны от нуля. Тогда существует единственное треугольное преобразование базисных векторов 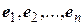, с помощью которого форму можно привести к каноническому виду.

Приведем формулы, по которым можно вычислить коэффициенты 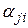искомого треугольного преобразования, и формулы для канонических коэффициентов :

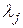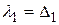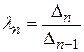, , …, . (4.19)

Пример 4 Найти канонический вид квадратичной формы

.

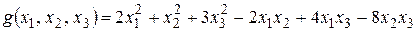методом Якоби.

Запишем матрицу квадратичной формы: 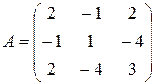. Тогда угловые миноры: 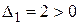, , 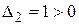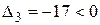. Канонический вид этой квадратичной формы будет иметь вид:

.

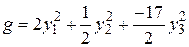Пример 5 Найти канонический вид квадратичной формы 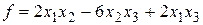методом Якоби.

Запишем матрицу квадратичной формы: 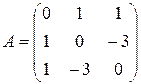. Тогда угловые миноры: 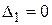, , 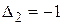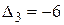. Этим методом данную квадратичную форму привести нельзя.