
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Занятия 9-10. Тема: Комбинированные задачи
 Эти занятия посвящены более сложным задачам, которые встречаются на олимпиадах разных уровней. Так как большая часть олимпиадных задач затрагивает небольшое число разделов математики, то школьникам, стремящимся к успеху, полезно знать темы этих разделов и видеть, что многие новые задачи часто не более чем малоузнаваемые вариации прежних.
Эти занятия посвящены более сложным задачам, которые встречаются на олимпиадах разных уровней. Так как большая часть олимпиадных задач затрагивает небольшое число разделов математики, то школьникам, стремящимся к успеху, полезно знать темы этих разделов и видеть, что многие новые задачи часто не более чем малоузнаваемые вариации прежних.
Задача 1. На стороне NP квадрата MNPQ взята точка A, а на стороне PQ – точка B так, что NA:AP = PB:BQ = 2:3. Точка L является точкой пересечения отрезков MA и NB. В каком отношении точка L делит отрезок MA?
Решение: проведем прямую AB, пусть она пересекает прямую MQ в точке F и пусть прямая NB пересекает прямую MQ в точке D (рис.41).
 APB ~
APB ~  FQB, тогда
FQB, тогда  , откуда QF=
, откуда QF= 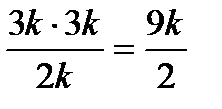 .
.
 NPB ~
NPB ~  DQB, тогда
DQB, тогда 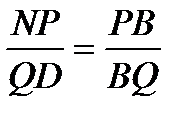 , откуда QD =
, откуда QD = 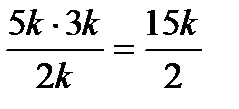 .
.
FD = QD – QF= 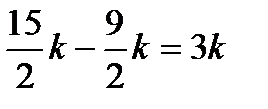 .
.
Из треугольника APB (прямоугольного) по теореме Пифагора AB = 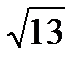 k.
k.
Из треугольника QBF (прямоугольного) по теореме Пифагора BF = 
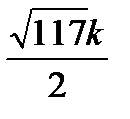 . Из треугольника AFM по теореме Менелая
. Из треугольника AFM по теореме Менелая
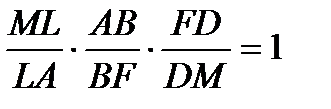 ,
, 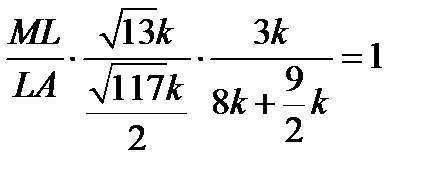 ,
, 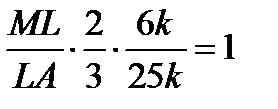 ,
, 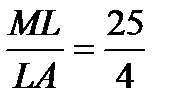 .
.
Ответ: 25: 4.
Задача 2. Дан параллелограмм ABCD. Точка M делит отрезок AD в отношении p, а точка N делит отрезок DC в отношении q. Прямые BM и AN пересекаются в точке S. Вычислите отношение AS:SN.
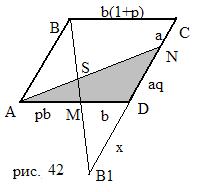 Решение:
Решение: 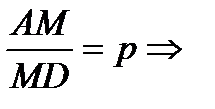
 если MD= b, то AM= pb;
если MD= b, то AM= pb; 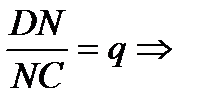
 если NC = a, то DN = aq.
если NC = a, то DN = aq.
Пусть B 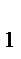 - точка пересечения прямых BM и CD.
- точка пересечения прямых BM и CD.
 MB
MB 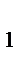 D ~
D ~  BB
BB 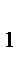 C, тогда
C, тогда 
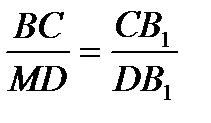 ;
;
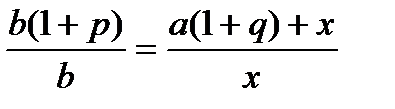 ;
;
1+p = 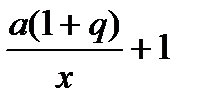 ; x =
; x = 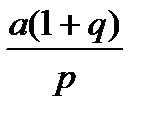 .
.
Прямая BB 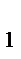 пересекает две стороны и продолжение третьей треугольника AND. По теореме Менелая
пересекает две стороны и продолжение третьей треугольника AND. По теореме Менелая 
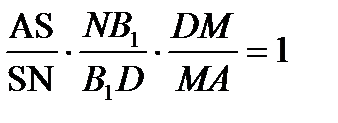 ,
, 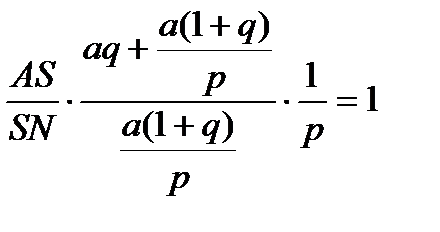 , откуда
, откуда 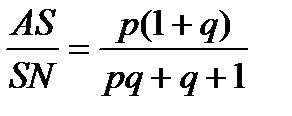 .
.
Ответ:  .
.
Задача 3. На сторонах AС и BC  взяты точки М и L так, что AM:MC=4:1, CL:LB=3:1. Отрезки AL и BM пересекаются в точке Q.
взяты точки М и L так, что AM:MC=4:1, CL:LB=3:1. Отрезки AL и BM пересекаются в точке Q.  .
.
 1) Найти
1) Найти 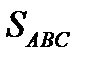 ; 2) На АВ взяли точку N так, что CN – медиана;
; 2) На АВ взяли точку N так, что CN – медиана; 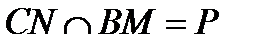 ,
, 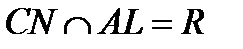 . Найти
. Найти 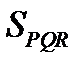 .
.
Решение:
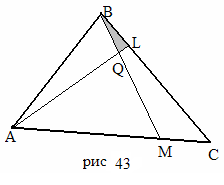
1) а) Рассмотрим 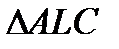 , BM – секущая (рис.43),
, BM – секущая (рис.43),
по теореме Менелая 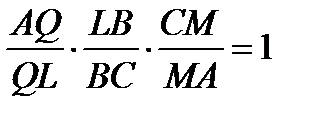 ,
, 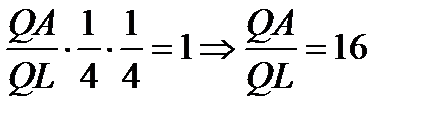
б) 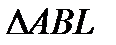 и
и 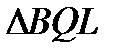 имеют равные высоты
имеют равные высоты 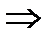
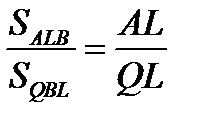 . Так как
. Так как 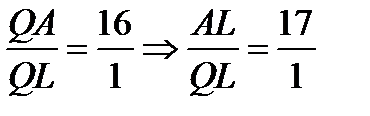 ,
,
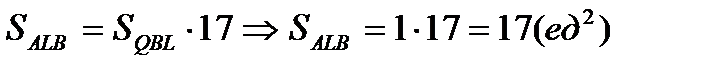
в) 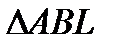 и
и 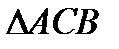 имеют равные высоты
имеют равные высоты 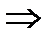
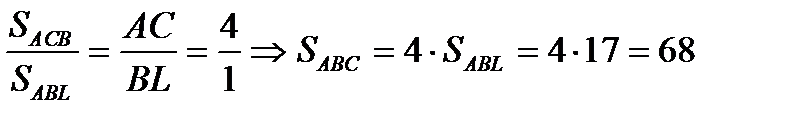
 2) CN-медиана
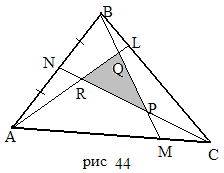
2) CN-медиана  AN=NB. Найдем
AN=NB. Найдем 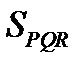 (рис. 44).
(рис. 44).
а) 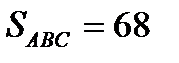 ,
, 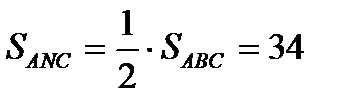 ;
;
б) 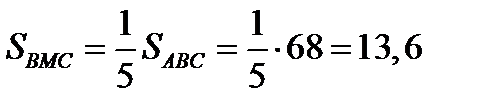 (имеют равные высоты),
(имеют равные высоты),
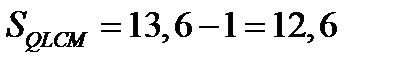 ;
; 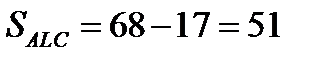 .
.
в) Рассмотрим  ABM и секущую NC.
ABM и секущую NC.
По теореме Менелая 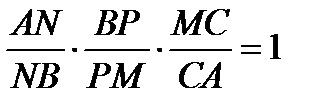 ,
, 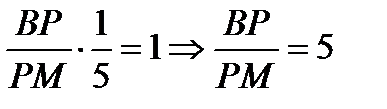
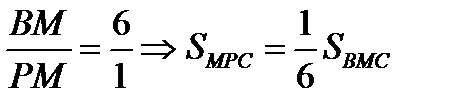 ,
, 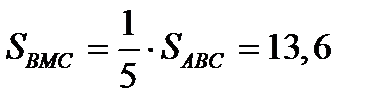 ,
, 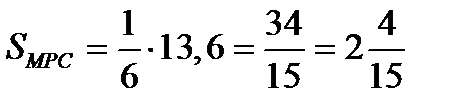
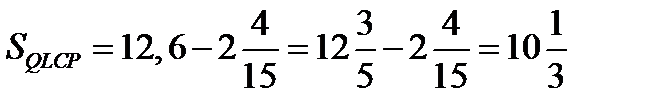 ,
, 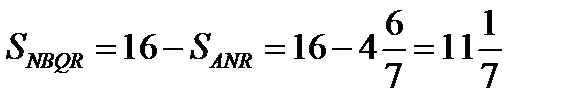
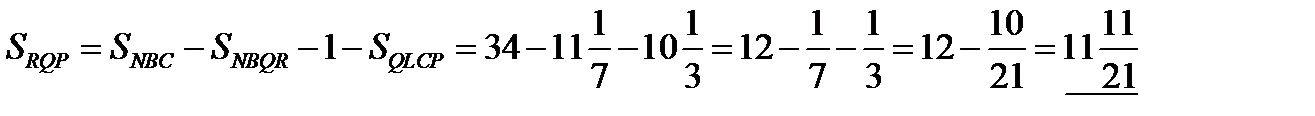 .
.
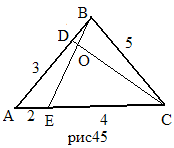 Ответ: 11
Ответ: 11 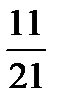 кв.ед.
кв.ед.
Задача 4. На стороне AB  ABC взята точка D, а на стороне AC – точка Е так, что длина AE=BD=2. Прямые
ABC взята точка D, а на стороне AC – точка Е так, что длина AE=BD=2. Прямые 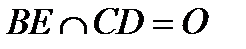 . Найти
. Найти 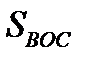 , если AB=BC=5, AC=6.
, если AB=BC=5, AC=6.
Решение: 1) 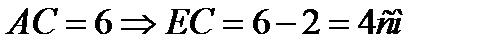 ,
, 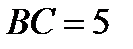 ,
, 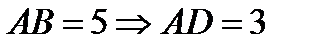
2) Рассмотрим  ABE, DC – секущая; D
ABE, DC – секущая; D 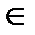 AB, O
AB, O 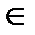 BE, C
BE, C 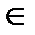 AE(рис.45).
AE(рис.45).
По теореме Менелая 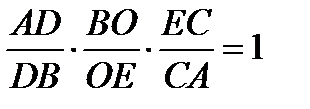 ,
, 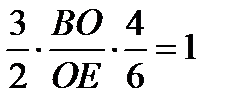 ;
; 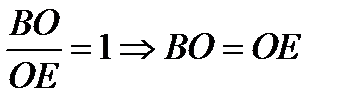 .
.
Значит, CO – медиана  BCE,
BCE, 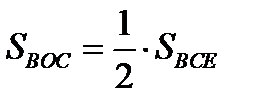 .
.
Из  ABC по теореме косинусов
ABC по теореме косинусов 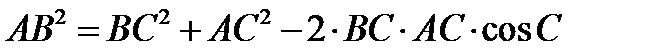
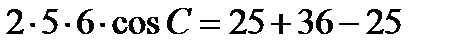 ,
, 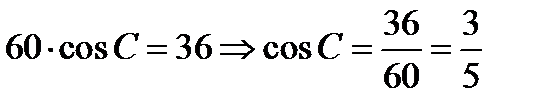
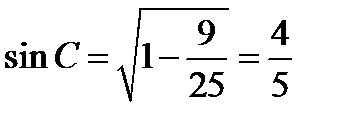
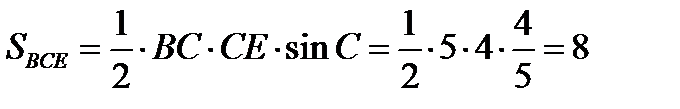 ;
; 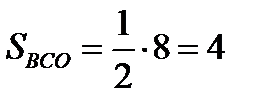 .
.
Ответ: 4.
Примечание 9: если на момент решения задачи теорема косинусов учащимся еще не известна, задачу 4 следует отложить до изучения теоремы.
Задача 5. На сторонахАВ, ВС и САтреугольника АВС отмечены точки 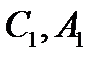 и
и  соответственно так, что отрезки
соответственно так, что отрезки 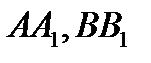 и
и 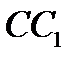 пересекаются в одной точке Q, расположенной внутри треугольника АВС. Пусть Р – точка пересечения отрезков
пересекаются в одной точке Q, расположенной внутри треугольника АВС. Пусть Р – точка пересечения отрезков 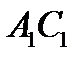 и
и 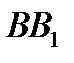 . Доказать, что
. Доказать, что 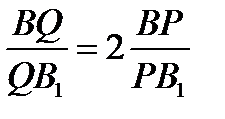 .
.
Доказательство. Эта задача может быть решена многими способами, мы разберем решение, использующее теоремы Менелая и Чевы, чрезвычайно полезные для решения задач такого типа.
 Если
Если 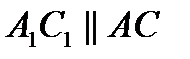
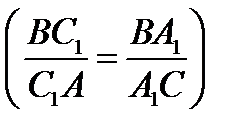 , то утверждение задачи может быть доказано достаточно легко. Рассмотрим случай, когда прямые
, то утверждение задачи может быть доказано достаточно легко. Рассмотрим случай, когда прямые  и
и 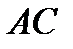 пересекаются в точке
пересекаются в точке
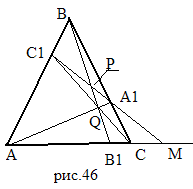
М (рис.46). По теореме Менелая для треугольников 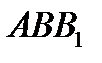 и
и  имеем:
имеем:
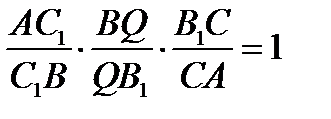 ,
, 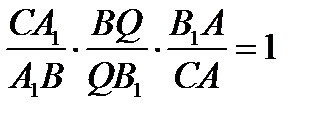 , откуда
, откуда 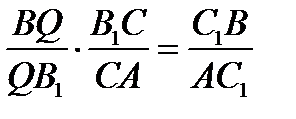 ,
,
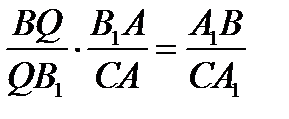 .
.
Складывая эти равенства, получаем 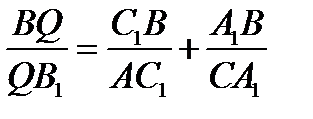 (1)
(1)
По теореме Менелая для треугольников 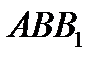 и
и 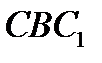 имеем:
имеем:
 ,
, 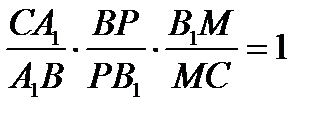
Учитывая, что 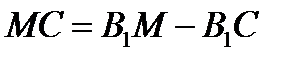 ,
,  , и складывая уравнения, получаем:
, и складывая уравнения, получаем:
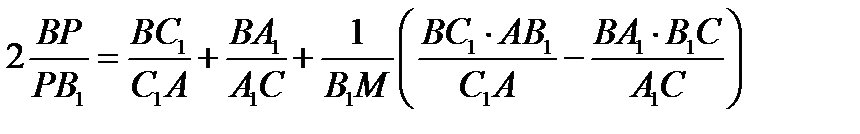 . Из теоремы Чевы для треугольника АВС следует, что
. Из теоремы Чевы для треугольника АВС следует, что 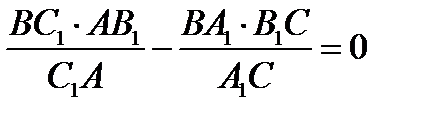 .
.
Поэтому 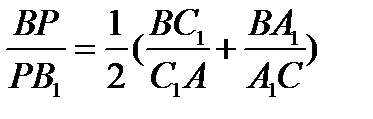 (2)
(2)
Сравнивая (1) и (2), получаем требуемое.
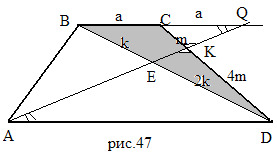 Задача 6. В трапеции ABCD с основаниями AD и BC через точку A проведена прямая, которая пересекает диагональ BD в точке E и боковую сторону CD в точке K, причем BE:ED=1:2, CK:KD=1:4. Найдите отношение длин оснований трапеции.
Задача 6. В трапеции ABCD с основаниями AD и BC через точку A проведена прямая, которая пересекает диагональ BD в точке E и боковую сторону CD в точке K, причем BE:ED=1:2, CK:KD=1:4. Найдите отношение длин оснований трапеции.
Решение. Пусть BC= a, AD= b. Необходимо найти 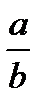 . Пусть BC
. Пусть BC  AK=Q (рис.47).
AK=Q (рис.47).
1) По теореме Менелая для  BCD и секущей AQ имеем
BCD и секущей AQ имеем 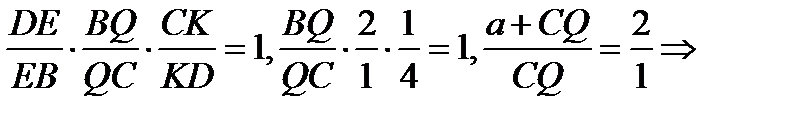 CQ= a, BC=CQ=a.
CQ= a, BC=CQ=a.
2)  CKQ ~
CKQ ~  DKA по двум углам, тогда
DKA по двум углам, тогда 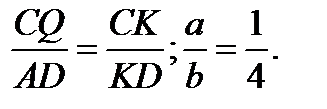 Так как а = BC, b =AD, то
Так как а = BC, b =AD, то 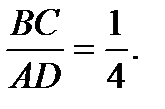
Ответ: 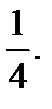
Date: 2015-07-02; view: 4827; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |