
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Занятия 3-4. Тема: Теорема Чевы и ее следствия. Применение теоремы Чевы и теоремы Менелая к задачам на доказательство
Цели: рассмотреть теорему Чевы, утверждение которой также связано с отрезками в треугольнике, некоторые следствия из нее; показать, как теоремы Чевы и Менелая применяются в задачах на доказательство.
Формулировка теоремы Чевы включает два взаимно обратных утверждения. Их можно рассмотреть как независимые теоремы.
Теорема (Чевы). Пусть точки A  ,B
,B  , C
, C  лежат соответственно на сторонах BC,AC и AB треугольника ABC, причем отрезки AA
лежат соответственно на сторонах BC,AC и AB треугольника ABC, причем отрезки AA  , BB
, BB  ,CC
,CC  пересекаются в одной точке.
пересекаются в одной точке.
Тогда  .
. 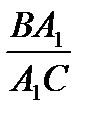 .
. 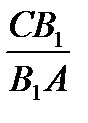 =1
=1
Доказательство теоремы проводится одним из способов, предложенных в главе I на с.6.
Исследование остальных случаев расположения точек - по усмотрению учителя, но в любом случае целесообразно сформулировать теорему Чевы и для случая внешней точки пересечения AA  , BB
, BB  ,CC
,CC  и для случая параллельных прямых, а также рассмотреть обратное утверждение.
и для случая параллельных прямых, а также рассмотреть обратное утверждение.
Теорема (Чевы, обратная). Пусть точки A  ,B
,B  , C
, C  лежат соответственно на сторонах BC,AC и AB треугольника ABC, причем
лежат соответственно на сторонах BC,AC и AB треугольника ABC, причем  .
. 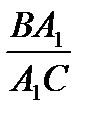 .
. 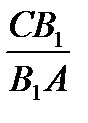 =1. Тогда отрезки AA
=1. Тогда отрезки AA  , BB
, BB  ,CC
,CC  пересекаются в одной точке. (Остальные случаи разъяснить).
пересекаются в одной точке. (Остальные случаи разъяснить).
Задача.
 На сторонах треугольника ABC взяты соответственно точки C
На сторонах треугольника ABC взяты соответственно точки C  , A
, A  ,B
,B  ,так, что AC
,так, что AC  : С
: С  B= 2:1, BA
B= 2:1, BA  :A
:A  C=1:3,
C=1:3,
BB 
 CC
CC 
 AA
AA  =O. Найти CB
=O. Найти CB  : B
: B  A.
A.
Решение:
Так как отрезки BB  , CC
, CC  , AA
, AA  пересекаются в одной точке O, то по теореме Чевы
пересекаются в одной точке O, то по теореме Чевы  .
. 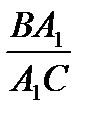 .
. 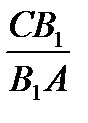 =1;
=1; 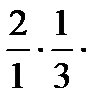
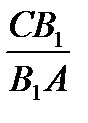 =1;
=1; 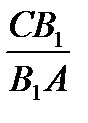 =
= 
Ответ: 3:2
Далее рассматриваются некоторые следствия из теоремы Чевы.
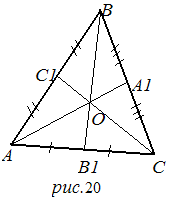 Следствие1. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Следствие1. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Доказательство. В учебной литературе доказательство этого утверждения проводится на основе подобных треугольников. Мы же проведем его, опираясь на теоремы Чевы и Менелая. Итак, пусть AA  , BB
, BB  ,CC
,CC  - медианы
- медианы  ABC (рис.20). Так как AC
ABC (рис.20). Так как AC  =C
=C  B, BA
B, BA  =A
=A  C, AB
C, AB  =B
=B  C, то
C, то  =1,
=1, 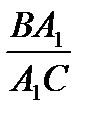 = 1,
= 1, 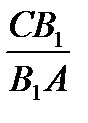 = 1. Тогда
= 1. Тогда  .
. 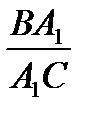 .
. 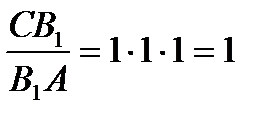 , т.е. для точек A
, т.е. для точек A  ,B
,B  ,C
,C  , лежащих на сторонах треугольника ABC, выполняется условие (
, лежащих на сторонах треугольника ABC, выполняется условие ( ); по теореме Чевы AA
); по теореме Чевы AA  , BB
, BB  ,CC
,CC  пересекутся в одной точке O (случай внутренней точки).
пересекутся в одной точке O (случай внутренней точки).
Рассмотрим  B
B  BC, точки A,O,A
BC, точки A,O,A  лежат на одной прямой, пересекающей стороны BB
лежат на одной прямой, пересекающей стороны BB  ,BC и продолжение стороны B
,BC и продолжение стороны B  C (в дальнейшем будем называть ее секущей). A
C (в дальнейшем будем называть ее секущей). A 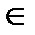 B
B  C, O
C, O  BB
BB  , A
, A 
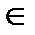 BC.
BC.
По теореме Менелая 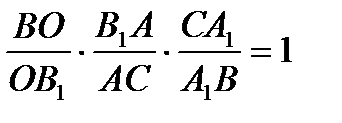 ,
, 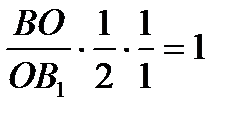

 =
= 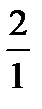 .
.
Применяя теорему Менелая для  A
A  AC и секущей BB
AC и секущей BB  (B
(B 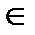 A
A  C, O
C, O 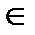 AA
AA  , B
, B 
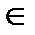 AC), получим, что
AC), получим, что  =
= 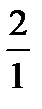 ; применяя теорему Менелая для
; применяя теорему Менелая для  С
С  BC и секущей AA
BC и секущей AA  , получим, что
, получим, что 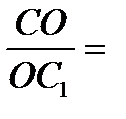
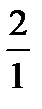 . Утверждение доказано.
. Утверждение доказано.
Следствие 2. Биссектрисы треугольника пересекаются в одной точке.
 Доказательство. Справедливость этого утверждения можно доказать, используя свойство биссектрисы:
Доказательство. Справедливость этого утверждения можно доказать, используя свойство биссектрисы:
так как AA  - биссектриса, то
- биссектриса, то 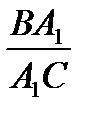 =
= 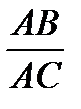 ; так как BB
; так как BB  - биссектриса, то
- биссектриса, то 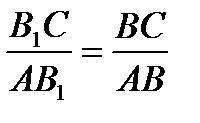 ;
;
так как СС  - биссектриса, то
- биссектриса, то  . Перемножая соответственно левые и правые части этих равенств, получим
. Перемножая соответственно левые и правые части этих равенств, получим 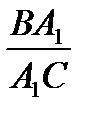 .
. 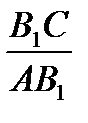 .
. 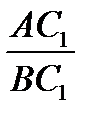 =
= 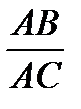 .
. 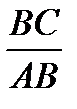 .
.  = 1, то есть для точек A
= 1, то есть для точек A  , B
, B  , C
, C  выполняется равенство Чевы, значит, AA
выполняется равенство Чевы, значит, AA  , BB
, BB  ,CC
,CC  пересекаются в одной точке.
пересекаются в одной точке.
Примечание 7: если учащимся известна теорема Чевы в форме синусов, то провести доказательство этого следствия можно следующим образом. Пусть AA  ,BB
,BB  ,CC
,CC  - биссектрисы
- биссектрисы  ABC (рис.21) Так как
ABC (рис.21) Так как 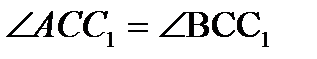 , то
, то 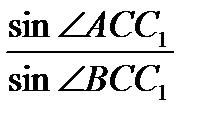 = 1; аналогично,
= 1; аналогично,  =1;
=1; 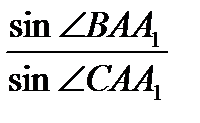 =1.
=1.
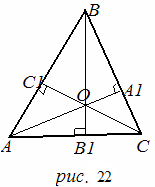 Перемножая эти равенства, получим условие (
Перемножая эти равенства, получим условие (
 ) теоремы Чевы в форме синусов. Значит, AA
) теоремы Чевы в форме синусов. Значит, AA  , BB
, BB  ,CC
,CC  пересекаются в одной точке.
пересекаются в одной точке.
Следствие3. Высоты треугольника (или их продолжения) пересекаются в одной точке (ортоцентре треугольника).
Доказательство: пусть AA  , BB
, BB  ,CC
,CC  - высоты
- высоты  ABC.
ABC.
1) Если  ABC остроугольный (рис. 22), то точки A
ABC остроугольный (рис. 22), то точки A  , B
, B  , C
, C  лежат на его сторонах.
лежат на его сторонах.  ACC
ACC  -прямоугольный, AC
-прямоугольный, AC  = AC cosA;
= AC cosA;
 BCC
BCC  - прямоугольный, BC
- прямоугольный, BC  = BC cosB;
= BC cosB;  BA
BA  A – прямоугольный, BA
A – прямоугольный, BA  = AB cosB;
= AB cosB;
 AA
AA  C- прямоугольный, A
C- прямоугольный, A  C=AC cosC; CB
C=AC cosC; CB  =CB cosC; AB
=CB cosC; AB  = AB cosA.
= AB cosA.
Тогда 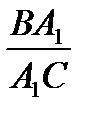 .
. 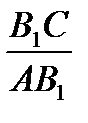 .
. 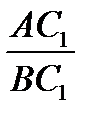 =
=  = 1. А так как условие (
= 1. А так как условие ( ) выполняется, то AA
) выполняется, то AA  , BB
, BB  , CC
, CC  пересекаются в одной точке.
пересекаются в одной точке.
Примечание 8: следствие 3 можно доказать, исходя из подобия треугольников. Можно предложить учащимся провести доказательство этим способом самостоятельно. (Действительно,  AA
AA  C~
C~  BB
BB  C по I признаку
C по I признаку 
 ; аналогично, из подобия
; аналогично, из подобия  CC
CC  B и
B и  AA
AA  B следует, что
B следует, что 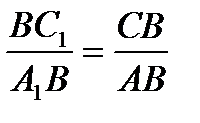 . И, наконец,
. И, наконец,
 BB
BB  A ~
A ~  CC
CC  A
A 
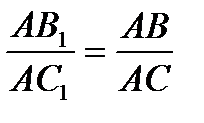 . Перемножая эти равенства, получим
. Перемножая эти равенства, получим

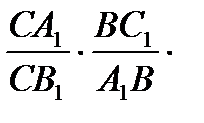
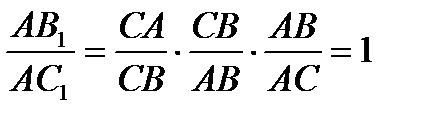 . Отсюда по теореме Чевы следует, что высоты остроугольного треугольника пересекаются в одной точке.[4, с.96])
. Отсюда по теореме Чевы следует, что высоты остроугольного треугольника пересекаются в одной точке.[4, с.96])
2) Пусть  ABC – тупоугольный (рис.23). Это случай внешней точки O. Из
ABC – тупоугольный (рис.23). Это случай внешней точки O. Из  ACC
ACC  AC
AC  =ACcosA; из
=ACcosA; из  С
С  BC C
BC C  B=CB cos (180
B=CB cos (180 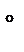 -
- 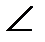 B)= -CB cosB (угол B тупой);
B)= -CB cosB (угол B тупой);
из  A
A  BA BA
BA BA  =AB cos(180
=AB cos(180 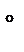 -
- 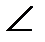 B)=-AB cosB; аналогично,
B)=-AB cosB; аналогично,
AB  =AB cosA; B
=AB cosA; B  C= BC cosC; A
C= BC cosC; A  C= AC cosC; CB
C= AC cosC; CB  =CBcosC.
=CBcosC.
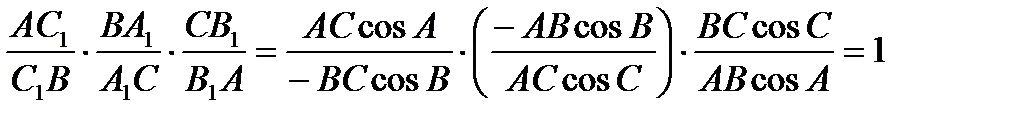 .
.
 Так как условие Чевы выполняется, то AA
Так как условие Чевы выполняется, то AA  , BB
, BB  , CC
, CC  пересекаются в одной точке или параллельны (глава1). Но если бы они были параллельны, то и перпендикулярные к ним прямые, то есть стороны треугольника ABC, были бы параллельны друг другу, но это не так. Значит, прямые AA
пересекаются в одной точке или параллельны (глава1). Но если бы они были параллельны, то и перпендикулярные к ним прямые, то есть стороны треугольника ABC, были бы параллельны друг другу, но это не так. Значит, прямые AA  ,BB
,BB  ,CC
,CC  пересекаются в одной точке.
пересекаются в одной точке.
 3) Если
3) Если  ABC прямоугольный,
ABC прямоугольный, 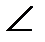 С=90
С=90 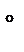 (рис.24), то очевидно, что высоты BC,AC,CC
(рис.24), то очевидно, что высоты BC,AC,CC  пересекаются в точке С. Следствие 3 доказано.
пересекаются в точке С. Следствие 3 доказано.
Следствие4. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Доказательство. Рассмотрим серединный  MNK(вершины-середины сторон
MNK(вершины-середины сторон  ABC)(рис.25). Тогда NK,NM,MK – средние линии треугольника ABC и по свойству средней линии NK
ABC)(рис.25). Тогда NK,NM,MK – средние линии треугольника ABC и по свойству средней линии NK  AC, NM
AC, NM  BC, KM
BC, KM  AB. Поэтому серединные перпендикуляры к сторонам треугольника ABC содержат высоты
AB. Поэтому серединные перпендикуляры к сторонам треугольника ABC содержат высоты  MNK. А в
MNK. А в  MNK по следствию 3 высоты пересекаются в одной точке, следовательно, серединные перпендикуляры пересекаются в одной точке.
MNK по следствию 3 высоты пересекаются в одной точке, следовательно, серединные перпендикуляры пересекаются в одной точке.
Таким образом, теорема Чевы дает возможность весьма просто доказать известные утверждения о четырех замечательных точках треугольника.
Рассмотрим еще одно следствие из теоремы Чевы.
 Следствие 5. Прямые, соединяющие вершины треугольника с точками, в которых вписанная окружность касается противоположных сторон, пересекаются в одной точке. Эта точка называется точкой Жергонна (рис.26).
Следствие 5. Прямые, соединяющие вершины треугольника с точками, в которых вписанная окружность касается противоположных сторон, пересекаются в одной точке. Эта точка называется точкой Жергонна (рис.26).
Доказательство. По свойству отрезков касательных, проведенных к окружности из одной точки, имеем AB  =AC
=AC  =x, C
=x, C  B=BA
B=BA  =y, A
=y, A  C=B
C=B  C=z.
C=z.
 , по теореме Чевы AA
, по теореме Чевы AA  , BB
, BB  , CC
, CC  пересекаются в одной точке.
пересекаются в одной точке.
Дополнительные задачи:
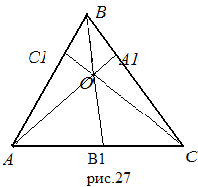 1. Используя теорему Чевы, доказать, что в произвольном треугольнике прямые, проходящие через вершины и делящие периметр треугольника пополам, пересекаются в одной точке. [4, с.94]
1. Используя теорему Чевы, доказать, что в произвольном треугольнике прямые, проходящие через вершины и делящие периметр треугольника пополам, пересекаются в одной точке. [4, с.94]
Доказательство: Пусть каждый из отрезков AA  , BB
, BB  ,CC
,CC  делит периметр треугольника ABC пополам (рис.27), то есть AB+BA
делит периметр треугольника ABC пополам (рис.27), то есть AB+BA  =A
=A  C+AC(1), B
C+AC(1), B  C+BC=AB
C+BC=AB  +AB(2), AC
+AB(2), AC  + СA=
+ СA=
=C  B+BC (3)
B+BC (3)
Сложим (1), (2), (3): AB +BA  +B
+B  C+ BC +AC
C+ BC +AC  + CA = A
+ CA = A  C+ AC + AB
C+ AC + AB  + AB + C
+ AB + C  B+ BC; BA
B+ BC; BA  +B
+B  C+AC
C+AC  =A
=A  C+AB
C+AB  +C
+C  B. Перенесем слагаемые в левую часть и сгруппируем:
B. Перенесем слагаемые в левую часть и сгруппируем:
(BA  - AB
- AB  ) + (B
) + (B  C - C
C - C  B) + (AC
B) + (AC  - A
- A  C)=0 (4). Вычитая из (1) равенство (2), получаем:
C)=0 (4). Вычитая из (1) равенство (2), получаем:
(AB+BA  )- (AB
)- (AB  +AB) = (A
+AB) = (A  C+AC)-(B
C+AC)-(B  C+BC) или BA
C+BC) или BA  - AB
- AB  = (AC- B
= (AC- B  C)-(BC- A
C)-(BC- A  C)=AB
C)=AB  - BA
- BA  = -(BA
= -(BA  - AB
- AB  ), откуда 2(BA
), откуда 2(BA  - AB
- AB  )= 0, BA
)= 0, BA  = AB
= AB  .
.
Аналогично доказывается, что CB  = С
= С  B, C
B, C  A = A
A = A  C.
C.
Тогда  .
. 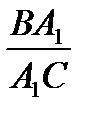 .
. 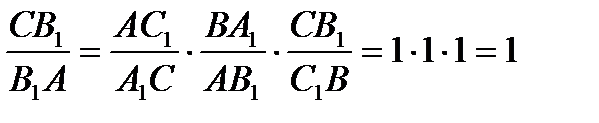 .
.
По теореме Чевы AA  , BB
, BB  ,CC
,CC  пересекаются в одной точке.
пересекаются в одной точке.
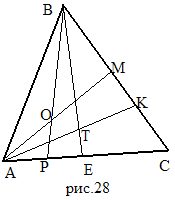 2. На стороне AC треугольника ABC взяты точки P и E, на стороне BC – точки M и K, причем AP: PE: EC= CK: KM: MB. Отрезки AM и BP пересекаются в точке O, отрезки AK и BE – в точке T. Докажите, что точки O, T и С лежат на одной прямой. [4, с.94]
2. На стороне AC треугольника ABC взяты точки P и E, на стороне BC – точки M и K, причем AP: PE: EC= CK: KM: MB. Отрезки AM и BP пересекаются в точке O, отрезки AK и BE – в точке T. Докажите, что точки O, T и С лежат на одной прямой. [4, с.94]
Дано:

 ABC; AP: PE: EC= CK: KM: MB =m:n:k
ABC; AP: PE: EC= CK: KM: MB =m:n:k
M, K  BC, P, E
BC, P, E 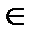 AC; AM
AC; AM  BP= O;
BP= O;
AK  BE= T
BE= T
Доказать: O, T, C  a
a
Доказательство. Пусть луч CT  AB=C
AB=C  , CO
, CO  AB=C
AB=C  . Докажем, что точки C
. Докажем, что точки C  и C
и C 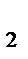 совпадают, это и будет означать, что O, T, C лежат на одной прямой.
совпадают, это и будет означать, что O, T, C лежат на одной прямой.
Так как CT  AB=C
AB=C  , BE
, BE  AK
AK  CC
CC  = T, то по теореме Чевы
= T, то по теореме Чевы  ;
;
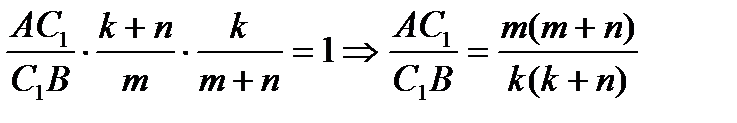 (1)
(1)
Так как CO  AB=C
AB=C  , AM
, AM  BP= O, то СС
BP= O, то СС 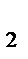
 BP
BP  AM=O, по теореме Чевы
AM=O, по теореме Чевы 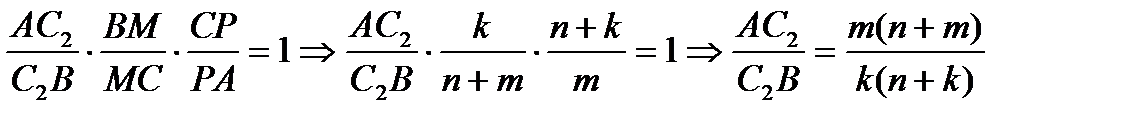 (2)
(2)
Из (1) и (2) следует, что 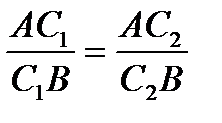 , то есть точки С
, то есть точки С  и C
и C  делят отрезок AB в одном и том же отношении, начиная от точки A, а значит, С
делят отрезок AB в одном и том же отношении, начиная от точки A, а значит, С  и C
и C  совпадают. А это означает, что точки O, T, C лежат на одной прямой.
совпадают. А это означает, что точки O, T, C лежат на одной прямой.
3. Прямая пересекает стороны AB,BC и продолжение стороны AC треугольника ABC соответственно в точках D,E,F.Доказать, что середины сторон отрезков DC, AE и BF лежат на одной прямой.(Теорема Гаусса.) Указание: воспользоваться теоремой Менелая, в качестве вершин данного треугольника взять середины сторон треугольника ABC, на сторонах и продолжениях которого лежат рассматриваемые точки.
4. Треугольники ABC и A  B
B  C
C  с попарно непараллельными сторонами расположены так, что прямые AA
с попарно непараллельными сторонами расположены так, что прямые AA  и A
и A  BB
BB  пересекаются в одной точке O. Доказать, что точки M,K,P пересечения прямых AB и A
пересекаются в одной точке O. Доказать, что точки M,K,P пересечения прямых AB и A  B
B  , BC и B
, BC и B  C
C  , AC и A
, AC и A  C
C  соответственно лежат на одной прямой. (Теорема Дезарга.) Указание: воспользоваться теоремой Менелая.
соответственно лежат на одной прямой. (Теорема Дезарга.) Указание: воспользоваться теоремой Менелая.
Задачи для самостоятельного решения.
1. Доказать, что середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон лежат на одной прямой. Указание: дважды используя теорему Менелая, доказать, что прямая, проходящая через точку пересечения диагоналей трапеции и через точку пересечения продолжений боковых сторон, проходит через середины оснований.
2. Доказать, что: а) биссектрисы внешних углов треугольника пересекают продолжения противоположных сторон треугольника в трех точках, расположенных на одной прямой; б) касательные к описанной около треугольника окружности в вершинах треугольника пересекают его противоположные стороны в трех точках, расположенных на одной прямой. Указание: воспользоваться теоремой Менелая.
3. На сторонах AB, BC и CA треугольника ABC взяты точки C  ,A
,A  и B
и B  соответственно. Пусть C
соответственно. Пусть C 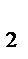 - точка пересечения прямых AB и A
- точка пересечения прямых AB и A  B
B  , A
, A  - точка пересечения прямых BC и B
- точка пересечения прямых BC и B  C
C  , B
, B  - точка пересечения прямых AC и A
- точка пересечения прямых AC и A  C
C  . Доказать, что если прямые AA
. Доказать, что если прямые AA  , BB
, BB  , CC
, CC  пересекаются в одной точке, то точки A
пересекаются в одной точке, то точки A  , B
, B  , C
, C 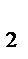 лежат на одной прямой. Указание: записав равенство Чевы для точек A
лежат на одной прямой. Указание: записав равенство Чевы для точек A  ,B
,B  ,C
,C  ; A
; A  ,B
,B  , C
, C 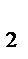 ; A
; A  , B
, B  , C
, C  ; A
; A  , B
, B  ,C
,C  ,получить, что для точек A
,получить, что для точек A  , B
, B  , C
, C  выполняется равенство Чевы; далее доказать, что или все три точки A
выполняется равенство Чевы; далее доказать, что или все три точки A  , B
, B  , C
, C  лежат на продолжениях сторон треугольника(так будет, если A
лежат на продолжениях сторон треугольника(так будет, если A  ,B
,B  ,C
,C  лежат на сторонах треугольника), или лишь одна находится на продолжении (если на сторонах треугольника одна из точек A
лежат на сторонах треугольника), или лишь одна находится на продолжении (если на сторонах треугольника одна из точек A  ,B
,B  ,C
,C  ) и воспользоваться теоремой Менелая.
) и воспользоваться теоремой Менелая.
4. Пусть ABCD – четырехугольник, P- точка пересечения BC и AD, Q – точка пересечения AC и BD, R – точка пересечения AB и CD. Доказать, что точки пересечения BC и QR, CA и RP, AB и PQ лежат на одной прямой. Указание: применить теорему Менелая к треугольникам ABD,BDC и DCA.
5. Окружность пересекает сторону AB треугольника ABC в точках C  и C
и C  , сторону BС – в точках A
, сторону BС – в точках A  и A
и A  , сторону CA- в точках B
, сторону CA- в точках B  и B
и B  . Доказать, что если прямые AA
. Доказать, что если прямые AA  ,BB
,BB  и CC
и CC  пересекаются в одной точке, то и прямые AA
пересекаются в одной точке, то и прямые AA  , BB
, BB 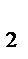 и CC
и CC 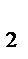 также пересекаются в одной точке. Указание: воспользоваться теоремой Чевы.
также пересекаются в одной точке. Указание: воспользоваться теоремой Чевы.
Занятия 5-6. Тема: Решение задач на пропорциональное деление отрезков в треугольнике.
Цели: овладение навыком решения задач с использованием теорем Менелая и Чевы; повышение уровня математической культуры учащихся, развитие их познавательных способностей.
Прежде всего надо отметить, что усвоение каждой темы школьного курса математики и развитие учащихся на том или ином уровне обеспечивается определенной системой упражнений и задач. [7,с.203] Выполнение математических упражнений является важнейшим видом учебной деятельности, в процессе которой школьниками усваивается математическая теория, развиваются их творческие способности и самостоятельность мышления.[15,с.3] Умение решать задачи самостоятельно, без посторонней помощи формируется автоматически, непроизвольно лишь у небольшой части учащихся. Для большинства же требуется специальная работа учителя в этом направлении. У школьников необходимо формировать умение решать и стандартные, и нестандартные задачи.
Наработать навыки решения стандартных задач на применение теорем Чевы и Менелая, а также организовать контроль за их выполнением поможет следующая таблица.
| Отнош. № зад. | а) 
| б) 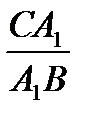
| в) 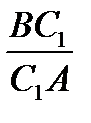
| г) 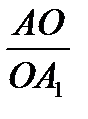
| д) 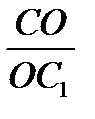
| е) 
|
| 1. | 
| 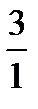
| 
| 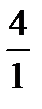
| 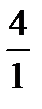
| 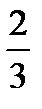
|
| 2. | 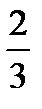
| 
| 
| 
| 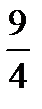
| 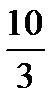
|
| 3. | 
| 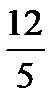
| 
| 
| 
| 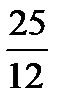
|
| 4. | 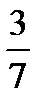
| 
| 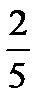
| 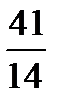
| 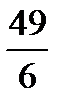
| 
|
| 5. | 
| 
| 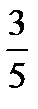
| 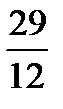
| 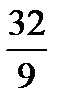
| 
|
| 6. | 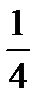
| 
| 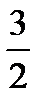 
|  
| 
| 
|
| 7. | 
| 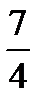
| 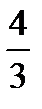
| 
| 
| 
|
| 8. | 
| 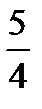
| 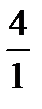
| 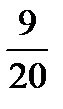
| 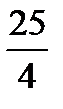
| 
|
Если три отрезка, соединяющие вершины A,B,C треугольника соответственно с точками A  ,B
,B  ,C
,C  лежащими на его сторонах, противоположных этим вершинам, пересекаются в точке O, то по любым двум из шести отношений длин отрезков, на которые точки A
лежащими на его сторонах, противоположных этим вершинам, пересекаются в точке O, то по любым двум из шести отношений длин отрезков, на которые точки A  ,B
,B  ,C
,C  делят стороны треугольника, а точка O- отрезки AA
делят стороны треугольника, а точка O- отрезки AA  ,BB
,BB  ,CC
,CC  , однозначно определяются оставшиеся отношения(с помощью теорем Менелая и Чевы).
, однозначно определяются оставшиеся отношения(с помощью теорем Менелая и Чевы).
 Две задачи из таблицы можно разобрать на занятии, остальные дать домой (используя таблицу, можно составить несколько вариантов заданий).
Две задачи из таблицы можно разобрать на занятии, остальные дать домой (используя таблицу, можно составить несколько вариантов заданий).
Далее можно организовать работу в группах.
Задача.
В  ABC на сторонах AB, BC,AC взяты точки C
ABC на сторонах AB, BC,AC взяты точки C  , A
, A  ,B
,B  соответственно. Отрезки BB
соответственно. Отрезки BB  ,AA
,AA  , CC
, CC  пересекаются в точке O. CB
пересекаются в точке O. CB  : B
: B  A=p, CA
A=p, CA  : A
: A  B=q.
B=q.
Найти:  .
.
Ученики делятся на 4 группы по количеству отношений, которые необходимо найти.
После того как задача окажется решена каждой группой, идет выступление представителей.
Решение: 1) Рассмотрим 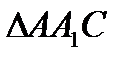 ; O
; O 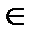 AA
AA  , B
, B 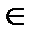 A
A  C, B
C, B 
 AC, O,B,B
AC, O,B,B  лежат на одной прямой (рис.29).
лежат на одной прямой (рис.29).
По теореме Менелая 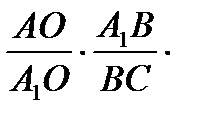
 ;
; 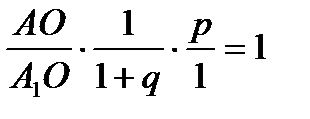
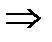
 .
.
2) Рассмотрим 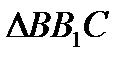 ; O
; O 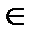 BB
BB  , A
, A 
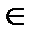 BC, A
BC, A 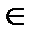 CB
CB  ; O, A
; O, A  , A лежат на одной прямой.
, A лежат на одной прямой.
По теореме Менелая  ;
; 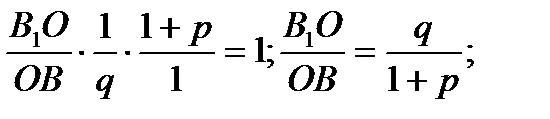
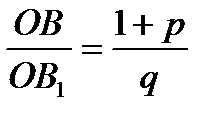 .
.
3) Рассмотрим  , по теореме Чевы
, по теореме Чевы  ;
; 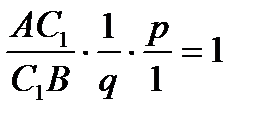 ;
;  .
.
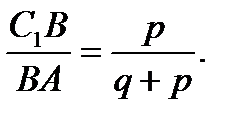 По теореме Менелая для
По теореме Менелая для  СС
СС  A и секущей BB
A и секущей BB 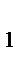
 ;
; 
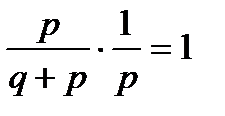 ;
;  .
.
4) Рассмотрим  , по теореме Чевы
, по теореме Чевы  ;
; 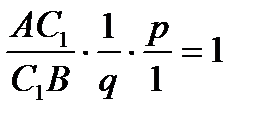 ;
;  .
.
Чтобы включить знания учащихся в систему, важно среди задач по теме иметь комплексные задачи, то есть задачи, при решении которых используются знания, полученные при изучении не только данной, но и предыдущих тем, а также при изучении других разделов математики. Поэтому полезными окажутся задачи 1-5.
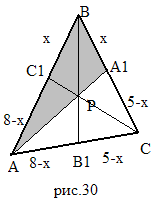 Задача 1.. В треугольнике ABC, описанном около окружности, AB = 8, BC = 5, AC = 4. Точки A
Задача 1.. В треугольнике ABC, описанном около окружности, AB = 8, BC = 5, AC = 4. Точки A 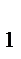 ,В
,В 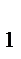 и C
и C  - точки касания, принадлежащие соответственно сторонам BC,AC и BA. Точка P - точка пересечения отрезков AA
- точки касания, принадлежащие соответственно сторонам BC,AC и BA. Точка P - точка пересечения отрезков AA 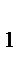 и CC
и CC 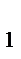 .
.
Найдите AP: PA 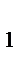 .
.
Решение: так как отрезки, соединяющие вершины треугольника с точками касания противоположных сторон, пересекаются в одной точке, то P 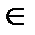 BB
BB 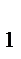 . Пусть C
. Пусть C 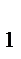 B=x, тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (рис. 30)
B=x, тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (рис. 30)
8 - x + 5 - x = 4, x = 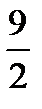 . Значит,C
. Значит,C 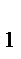 B = BA=
B = BA=  ; A
; A 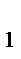 C = 5 –
C = 5 –  =
= 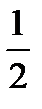 , AC = 8 –
, AC = 8 –  =
=  .
.
В треугольнике ABA 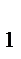 прямая C
прямая C 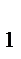 C пересекает две его стороны и продолжение третьей стороны. По теореме Менелая
C пересекает две его стороны и продолжение третьей стороны. По теореме Менелая



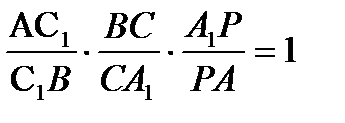 ,
,  ,
,  =
= 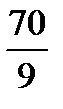 .
.
Ответ: 70: 9.
Задача 2. Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.
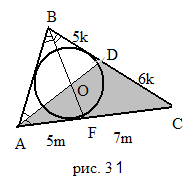 Решение: пусть в треугольнике ABC AB = 5, BC = 7, AC = 6. Угол BAC лежит против большей стороны в треугольнике ABC, значит, угол BAC – больший угол треугольника. Центр вписанной окружности треугольника лежит на пересечении биссектрис. Пусть O -точка пересечения биссектрис. Необходимо найти AO:OD. Так как AD – биссектриса треугольника ABC, то
Решение: пусть в треугольнике ABC AB = 5, BC = 7, AC = 6. Угол BAC лежит против большей стороны в треугольнике ABC, значит, угол BAC – больший угол треугольника. Центр вписанной окружности треугольника лежит на пересечении биссектрис. Пусть O -точка пересечения биссектрис. Необходимо найти AO:OD. Так как AD – биссектриса треугольника ABC, то 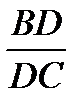 =
=  , то есть BD = 5k, DC = 6k. Так как BF – биссектриса треугольника ABC, то
, то есть BD = 5k, DC = 6k. Так как BF – биссектриса треугольника ABC, то 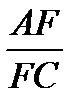 =
= 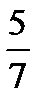 , то есть AF = 5m, FC = 7m.
, то есть AF = 5m, FC = 7m.
Прямая BF пересекает две стороны и продолжение третьей треугольника ADC.
По теореме Менелая
 .
. 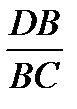 .
.  = 1,
= 1,  =
= 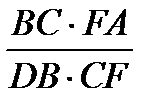 =
= 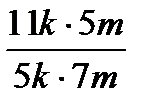 =
= 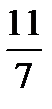
Ответ: 11:7.
 Задача 3. В треугольнике ABC, описанном около окружности, AB =13, BC = 12, AC = 9, A
Задача 3. В треугольнике ABC, описанном около окружности, AB =13, BC = 12, AC = 9, A 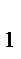 и C
и C 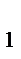 - точки касания, лежащие соответственно на сторонах BC и AB. Q –точка пересеченияотрезков AA
- точки касания, лежащие соответственно на сторонах BC и AB. Q –точка пересеченияотрезков AA 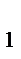 и BH,где BH- высота. Найдите отношение BQ:QH.
и BH,где BH- высота. Найдите отношение BQ:QH.
Решение:
треугольник ABC – разносторонний, значит, точка H не совпадает с точкой касания. Обозначим точку касания, лежащую на стороне AC, буквой B 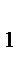 .
.
1. Пусть C 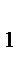 B = x, тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (рис.32):
B = x, тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (рис.32):
BA 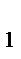 =x, A
=x, A 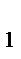 C=B
C=B 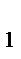 C=12-x, AC
C=12-x, AC 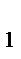 =AB
=AB 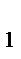 =13-x. Тогда (13 – x) + (12 – x) = 9, x=8. Значит, C
=13-x. Тогда (13 – x) + (12 – x) = 9, x=8. Значит, C 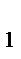 B =BA
B =BA 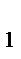 = 8, AC
= 8, AC 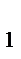 =AB
=AB 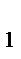 = 5, CA
= 5, CA 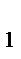 =CB
=CB 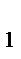 =4.
=4.
2. По формуле Герона
S 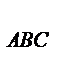 =
= 
 = 4
= 4  ,
,
S 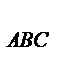 =
= 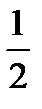
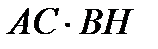 , BH =
, BH = 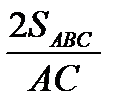 , BH =
, BH = 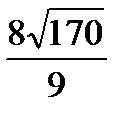 .
.
3. Из треугольника ABH (прямоугольного) по теореме Пифагора
AH = 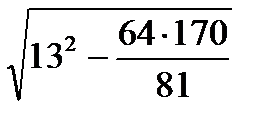 =
=  .
.
4. В треугольнике CBH прямая AA  пересекает две его стороны и продолжение третьей. По теореме Менелая
пересекает две его стороны и продолжение третьей. По теореме Менелая
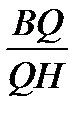 .
. 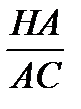 .
. 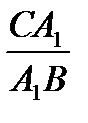 =1,
=1, 
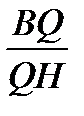 .
.  .
.  =1,
=1, 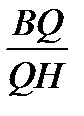 .
.  .
.  =1,
=1, 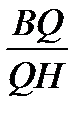 =
=  .
.
Ответ: 162:53.
 Задача 4. В треугольнике ABC, площадь которого равна 6, на стороне AB взята точка K, делящая эту сторону в отношении AK:BK = 2:3, а на стороне AC – точка L, делящая AC в отношении AL: LC = 5:3. Точка Q пересечения прямых CK и BL удалена от прямой AB на расстояние
Задача 4. В треугольнике ABC, площадь которого равна 6, на стороне AB взята точка K, делящая эту сторону в отношении AK:BK = 2:3, а на стороне AC – точка L, делящая AC в отношении AL: LC = 5:3. Точка Q пересечения прямых CK и BL удалена от прямой AB на расстояние  . Найдите длину стороны AB.
. Найдите длину стороны AB.
Решение:
1. Треугольники ABL и ABC имеют одинаковую высоту, проведенную из вершины B.
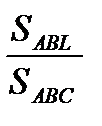 =
= 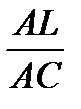 =
= 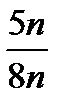 =
=  , тогда S
, тогда S 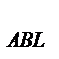 =
=  6 =
6 = 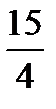 .
.
2. Прямая KC пересекает в треугольнике ABL две стороны и продолжение третьей. По теореме Менелая
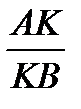 .
. 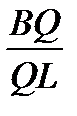 .
. 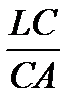 = 1,
= 1,  .
.  .
.  = 1,
= 1, 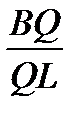 =
=
((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228269']=__lxGc__['s']['_228269']||{'b':{}})['b']['_698163']={'i':__lxGc__.b++};
Date: 2015-07-02; view: 9703; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |