
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Прямолинейные образующие на поверхности гиперболического параболоида
Рассмотрим уравнение гиперболического параболоида:
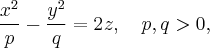
для удобства сделаем замену  и
и 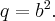 Тогда уравнение запишется в виде
Тогда уравнение запишется в виде
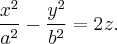
Разложим на множители:
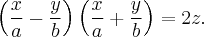
Аналогично с предварительными соображениями получаем уравнения двух семей прямолинейных образующих гиперболического параболоида:
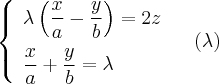 и
и 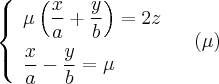
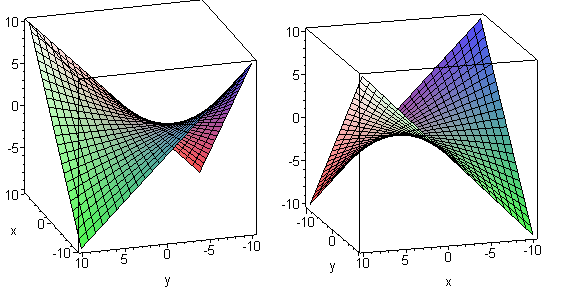
Теорема. На поверхности гиперболического параболоида лежат две семьи прямых, которые имеют следующие свойства:
· через любую точку гиперболического параболоида проходит ровно одна прямая с каждой семьи;
· любые две образующие из разных семей пересекаются;
· любые две прямые с одной семьи является скрещивающимися;
· любые три прямые с одной семьи параллельные некоторой плоскости.
Доказательство можно посмотреть в методичке.
Пример. Найдите уравнение плоскости, параллельной плоскости  и пересекает гиперболический параболоид
и пересекает гиперболический параболоид 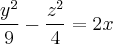 по двум прямолинейным образующим. Найдите канонические уравнения этих образующих.
по двум прямолинейным образующим. Найдите канонические уравнения этих образующих.
Запишем уравнение параллельной плоскости 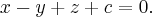 Найдем ее пересечение с гиперболическим параболоидом.
Найдем ее пересечение с гиперболическим параболоидом.
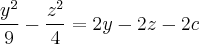
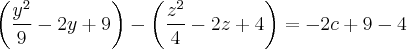
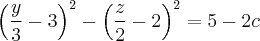
Эта кривая второго порядка распадается на пару прямых, которые пересекаются, если 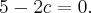 есть
есть 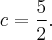 Итак плоскость, которую мы ищем, имеет уравнение
Итак плоскость, которую мы ищем, имеет уравнение 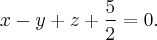 Две прямые, лежат в этой плоскости и является пересечением с параболоидом:
Две прямые, лежат в этой плоскости и является пересечением с параболоидом:
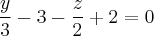 и
и 
или 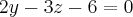 и
и 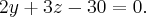
Уравнения этих прямых в пространстве:
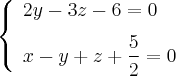 и
и 
Найдем канонические уравнения. Для первой прямой:
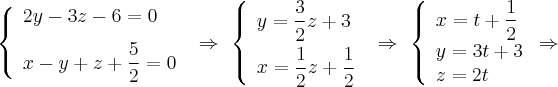
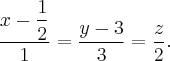
Для второй прямой:
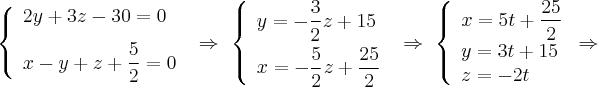
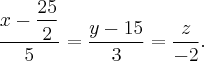
Date: 2015-07-01; view: 8675; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |