Круговые сечения трехосного эллипсоида

Заметим, что на каноническом эллипсоиде

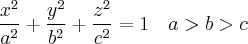
сечение дает эллипс с большой полуосью 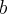на оси 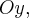а сечение 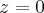дает эллипс с малой полуосью 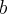на оси 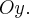Итак, существует сечение, где полуоси уровне и равны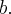

Рассмотрим плоскость, натянутую на векторы:

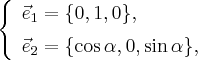
которая проходит через начало координат. Векторное уравнение этой плоскости: 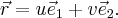Векторы перпендикулярны и имеют единичную длину, поэтому в плоскости векторы и образуют базисные векторы декартовой прямоугольной системы координат. Итак, - координаты относительно этой системы координат. Запишем параметрическое уравнение плоскости

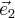
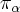
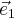
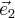
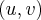
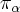
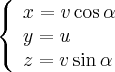
и найдем ее пересечение с эллипсоидом:

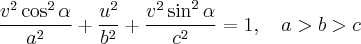
или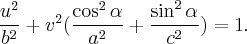

В плоскости сечения параметры 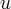и есть декартовыми прямоугольными координатами. Поэтому полученный сечение является эллипсом. Покажем, что среди этих эллипсов является круг. Будем подбирать 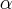так, чтобы

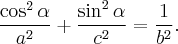
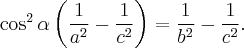
Итак,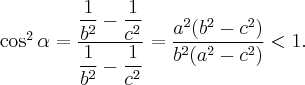

Действительно,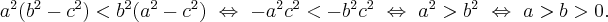

Упражнение. Показать, что любая плоскость параллельна найденной, пересекает эллипсоид по кругам.

Точка на эллипсоиде, в которой касательная плоскость параллельна круговым сечениям называется оболочною точкой, или коротко ОМБИЛИК.

Упражнение. Найти омбиличны точки на поверхности трехосного эллипсоида. Исследовать их поведение в зависимости от соотношения осей.

Гиперболоиды.

Однополостный гиперболоид

В плоскости 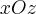возьмем гиперболу

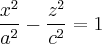
и будем вращать ее вокруг оси 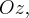получим поверхность с уравнением

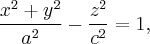
которая называется Однополостный гиперболоидом вращения.

Итак, однополостный гиперболоид вращения получается вращением гиперболы вокруг воображаемой оси.

Если мы будем проводить сжатие пространства вдоль оси 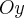с коэффициентом 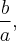то с однополостного гиперболоида вращения мы получим так называемый трехосный однополостный гиперболоид:

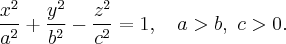
Итак имеем такое
определение. Геометрическое место точек пространства, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяет уравнению

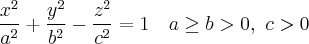
называется Однополостный гиперболоидом. Данное уравнение называется каноническим уравнением однополостного гиперболоида, а соответствующая система координат называется канонической. Если 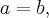то поверхность называется Однополостный гиперболоидом вращения.

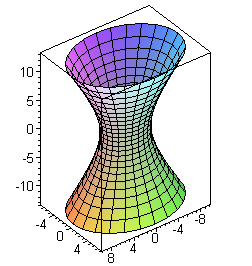
Однополостный гиперболоид имеет три плоскости симметрии - координатные плоскости, три оси симметрии - оси координат и единый центр симметрии -начало координат.

Сечения однополостного гиперболоида плоскостями 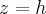проецируются на плоскость 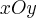в семью эллипсов

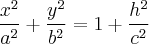
с полуосями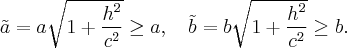

Сечения однополостного гиперболоида плоскостями 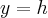проецируются на плоскость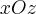

· при 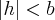в семью гипербол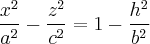

с полуосями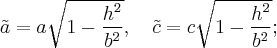

· при 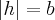в пару прямых, пересекающихся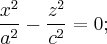

· при 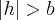в самосопряжённых гипербол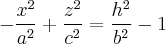

с полуосями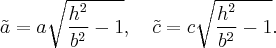

Свойства сечений плоскостями аналогичные свойствам сечений плоскостями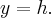

Двуполостные гиперболоид.

В плоскости 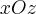возьмем сопряженную гиперболу

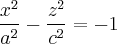
и будем вращать ее вокруг оси 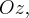получим поверхность с уравнением

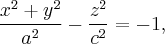
которая называется двуполостные гиперболоидом вращения.

Итак, двуполостные гиперболоид вращения получается вращением гиперболы вокруг действительной оси.

Если мы будем проводить сжатие пространства вдоль оси 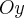с коэффициентом 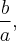то с двуполостные гиперболоида вращения мы получим так называемый трехосный двуполостные гиперболоид:

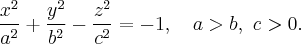
Итак имеем такое

Определение. Геометрическое место точек пространства, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяет уравнению

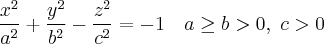
называется двуполостные гиперболоидом. Данное уравнение называется каноническим уравнением двуполостные гиперболоида, а соответствующая система координат называется канонической. Если 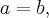то поверхность называется двуполостные гиперболоидом вращения.

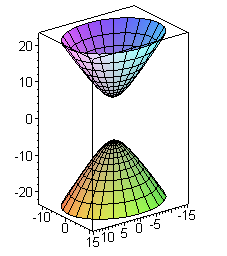
Двуполостные гиперболоид имеет три плоскости симметрии - координатные плоскости, три оси симметрии - оси координат и единый центр симметрии -начало координат.

Сечения двуполостные гиперболоида плоскостями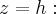

· при 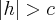проецируются на плоскость 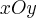в семью эллипсов

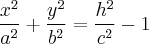
с полуосями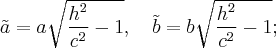

· при 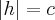плоскость 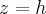соприкасается поверхности в единой точке - вершине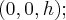

· при 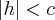плоскость 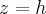не имеет общих точек с двуполостные гиперболоидом.

Сечения двуполостные гиперболоида плоскостями 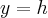проецируются на плоскость 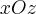в семью гипербол

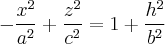
с полуосями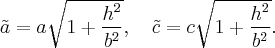

Свойства сечений плоскостями аналогичные свойствам сечений плоскостями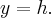

Упражнение. Найти круговые сечения трехосного двуполостные гиперболоида и омбилични точки на нем. Исследовать поведение омбиличних точек в зависимости от соотношения осей.

Параболоид.

Эллиптический параболоид.

В плоскости 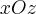возьмем параболу

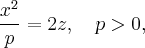
и будем вращать ее вокруг оси 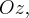получим поверхность с уравнением

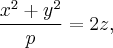
которая называется параболоидом вращения.

Эллиптический параболоид

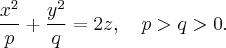
получается из параболоида вращения сжатием вдоль оси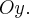

Определение. Геометрическое место точек пространства, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяет уравнению

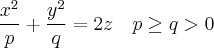
называется эллиптическим параболоидом. Данное уравнение называется каноническим уравнением эллиптического параболоида, а соответствующая система координат называется канонической. Если 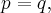то поверхность называется эллиптическим параболоидом вращения, или просто параболоидом вращения.

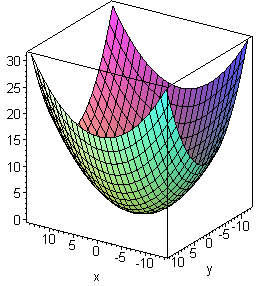
Эллиптический параболоид имеет две плоскости симметрии - координатные плоскости 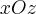и одну ось симметрии - ось и не имеет ни центра симметрии.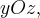

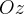
Сечения эллиптического параболоида плоскостями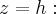

· при 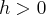проецируются на плоскость 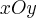в семью эллипсов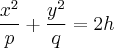

с полуосями

· при 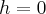плоскость 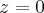соприкасается поверхности в единой точке 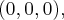которая называется вершиной эллиптического параболоида;

· при 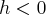плоскость 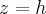не имеет общих точек с эллиптическим параболоидом.

Сечения эллиптического параболоида плоскостями 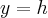проецируются на плоскость 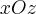в семью конгруэнтных парабол

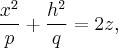
полученные сдвигом "вверх" параболы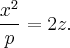

Свойства сечений эллиптического параболоида плоскостями аналогичные свойствам сечений плоскостями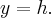

Эллиптический параболоид является поверхностью переноса, образованной парабола мы 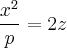и 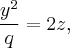которые лежат во взаимно ортогональных координатных плоскостях.

Гиперболический параболоид.

Еще одной поверхностью переноса второго порядка является гиперболический параболоид, он образуется парабола мы 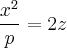и 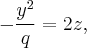которые лежат во взаимно ортогональных координатных плоскостях.

Определение. Геометрическое место точек пространства, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяет уравнению

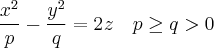
называется гиперболическим параболоидом. Данное уравнение называется каноническим уравнением гиперболического параболоида, а соответствующая система координат называется канонической.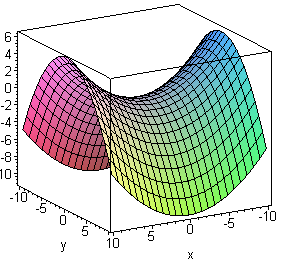

Гиперболический параболоид имеет две плоскости симметрии - координатные плоскости 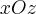и одну ось симметрии - ось и не имеет ни центра симметрии.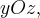

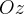
Сечения гиперболического параболоида плоскостями 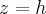проецируются на плоскость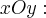

· при 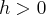в сім'ю гіпербол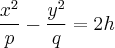

с полуосями

· при 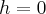в две прямые, пересекающиеся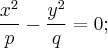

· при 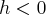в сім'ю гіпербол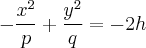

с полуосями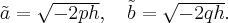

Сечения эллиптического параболоида плоскостями 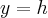проецируются на плоскость 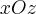в семью конгруэнтных парабол

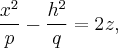
полученные сдвигом "вниз" параболы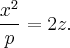

Сечения эллиптического параболоида плоскостями проецируются на плоскость 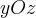в семью конгруэнтных парабол

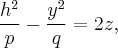
полученные сдвигом "вверх" параболы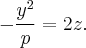

Date: 2015-07-01; view: 3656; Нарушение авторских прав