
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Оптическая свойство параболы
Утверждение. Касательная к параболе образует равные углы с осью 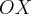 и с фокальным радиусом
и с фокальным радиусом 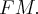
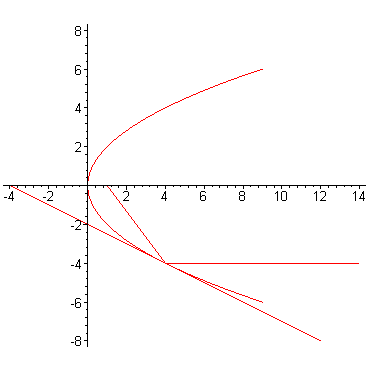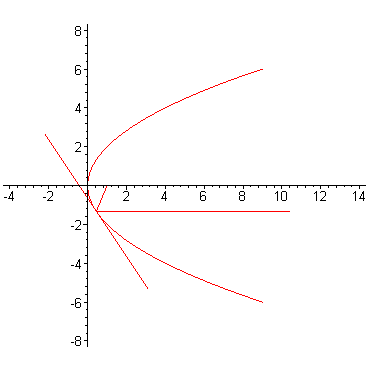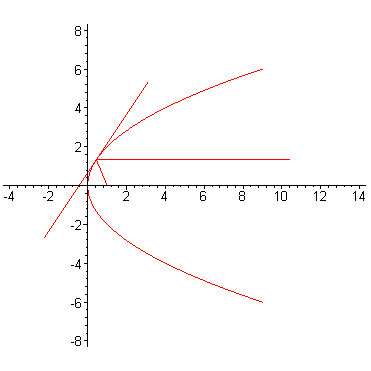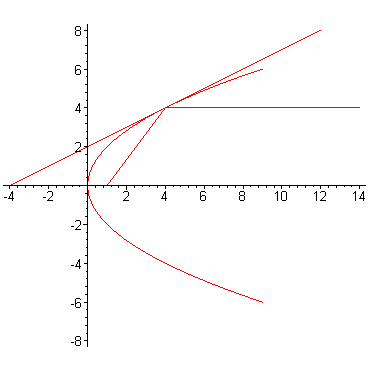
Доказательство. Обозначим через - точку пересечения касательной с осью Из уравнения касательной следует, что ее координаты Итак, Таким образом, треугольник равнобедренный. 
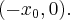
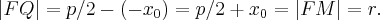
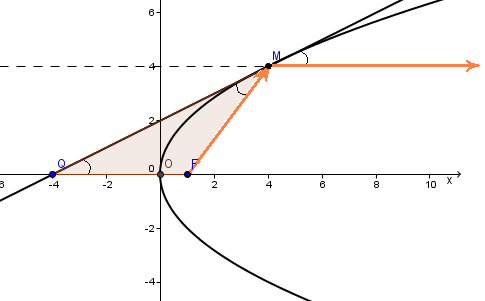
Если представить параболу как зеркальную кривую, то по законам оптики луч света, выпущенный из фокуса, после отражения от параболы пойдет на бесконечность параллельно фокальной оси. И наоборот, пучок лучей, параллельных фокальной оси, соберется в фокусе. Собственно, по этой причине указанное свойство называется оптической. Фокусное ось иногда называется оптической осью параболы. Оптическая свойство имеет очевидные технические применения.
Эллипс.
Г.М.Т, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяют уравнению
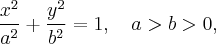
называется эллипсом. Данное уравнение называется каноническим уравнением эллипса, а соответствующая система координат называется канонической.

Геометрическими характеристиками эллипса являются:
· две оси симметрии 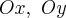 и один центр симметрии
и один центр симметрии 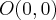 ;
;
· Величины 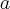 и
и 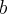 , которые называются соответственно большой и малой полуосями;
, которые называются соответственно большой и малой полуосями;
· величина 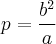 , которая называется фокальным параметром;
, которая называется фокальным параметром;
· величина 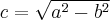 ;
;
· точки 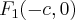 и
и 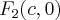 , которые называются левым и правым фокусами (очаговыми точками) соответственно;
, которые называются левым и правым фокусами (очаговыми точками) соответственно;
· величина 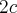 , которая называется фокусным расстоянием;
, которая называется фокусным расстоянием;
· величина 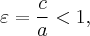 которая называется эксцентриситетом;
которая называется эксцентриситетом;
· две директрисы:
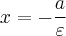 - левая, или
- левая, или 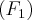 директриса,
директриса,
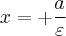 - права, или
- права, или 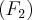 директриса;
директриса;
· точки  называемых вершинами эллипса.
называемых вершинами эллипса.
Представление о форме эллипса дает следующее
Утверждение. Эллипс
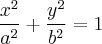
можно получить сжатием круга
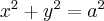
вдоль одной из двух взаимно перпендикулярных осей симметрии круга.
Доказательство. Направим вдоль пары взаимно перпендикулярных диаметров круга радиуса 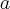 координатные оси
координатные оси 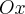 и
и 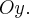 Тогда уравнение окружности запишется в виде
Тогда уравнение окружности запишется в виде 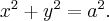
Будем проводить сжатия вдоль оси 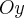 с коэффициентом
с коэффициентом 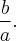 Пусть точка с координатами
Пусть точка с координатами  принадлежит кругу, то есть
принадлежит кругу, то есть 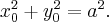 Тогда точка с координатами
Тогда точка с координатами 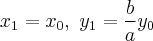 принадлежит эллипсу. Действительно,
принадлежит эллипсу. Действительно,
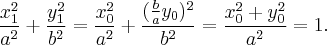
Date: 2015-07-01; view: 3601; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |