Динамическое программирование. Принцип оптимальности Беллмана. Уравнение Беллмана.

Многие процессы проектирования систем управления, как и сам процесс проектирования, являются многоэтап­ными (многошаговыми). Весьма эффективным методом оптимизации сложных многошаговых процессов является динамическое программирование (планиро­вание). Этот метод был предложен и развит американским математиком Р. Беллманом в 60-х годах нашего столетия. В основу метода положен интуитивно очевидный принцип, названный принципом оптимальности, который можно сформулировать следующим образом: оптимальное поведение в данный момент времени определяется только состоянием объекта (системы) в этот момент вре­мени и конечным желательным состоянием и не зависит от поведения в про­шлом.

При использовании этого метода можно заменить исходную сложную за­дачу отыскания многошагового управления последовательным решением неко­торого количества существенно более простых одношаговых задач оптимиза­ции. Основной метол динамического программирования - метод рекуррентных соотношений, базирующийся на принципе оптимальности.

Рис.2.3.2. Геометрическая интерпретация динамического программирования.

Задача динамического программирования формулируется следующим образом: из множества допустимых управлений необходимо найти такое 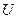, которое переводит объект (систему) из начального состояния в конеч­ное так, чтобы целевая функция (критерий качества) принимала макси­мальное значение

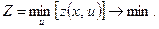
Оптимизация управления многошагового процесса, таким образом, сво­дится к нахождению такой последовательности управлений 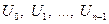которая обеспечивает достижение максимального значения целевой функции или, что то же, минимального значения затрат (потерь, штрафов), т. е.

По определению.

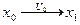
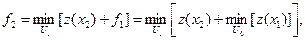
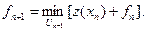
В общем случае для (n–1)-шагового процесса, начинающегося с состояния , получим уравнение Беллмана

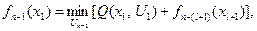
представляющее собой рекуррентное соотношение, позволяющее последова­тельно определять оптимальное уравнение на каждом шаге управляемого про­цесса.

Характерной особенностью метода динамического программирования яв­ляется совмещение простоты решения задач оптимизации на отдельном шаге с учетом самых отдаленных последствий этого шага. Действительно, выбор управления на каждом шаге производится не только исходя из минимизации потерь (или максимизации выигрыша) на данном шаге, т. е. минимизации вели­чины 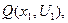но и из минимизации суммарных потерь 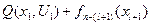на всех последующих шагах.

В уравнении Беллмана n–1 означает число шагов до конца процесса. Вве­дем новые обозначения: n–1=K, 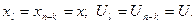Здесь х и U означают со­стояние объекта и управление за К шагов до конца процесса.

С учетом новых обозначений уравнение Беллмана представим в виде

здесь 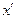означает то состояние, к которому переходит объект из состояния при применении управления U.

Для расчетов на ЭВМ последнее соотношение удобнее записать в виде

Значения 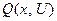вычисляют заранее и представляют в виде таблицы, ко­торая хранится в памяти ЭВМ.

Метод динамического программирования применим не для всех задач. А лишь для задач с определенной структурой зависимости управления на различ­ных шагах процесса и для целевых функций специального вида - аддитивных функционалов от траектории.

Date: 2016-07-18; view: 897; Нарушение авторских прав