Принцип максимума Понтрягина. Графическая иллюстрация метода.

Принцип максимума Понтрягина (основные результаты получены в 1956-1961 гг. Л.С. Понтрягиным, Б.Г. Болтянским, Р.В. Гамрекелидзе и Е.Ф. Мищенко) представляет собой обобщение методов вариационного исчисления и позволяет решать задачи при наличии ограничений в виде неравенств.

Необходимо найти функции 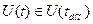так, чтобы функционал принял максимальное значение:

Здесь U(t) – вектор-функция управления, переводящая фазовую точку из на­чального положения в конечное 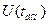– область допустимых значений вектор-функции управления; знак 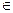– включение; – вектор состояния (по­ложения) системы, характеризуемый фазовыми координатами.

Связи между фазовыми координатами и управлениями описываются сис­темой дифференциальных уравнений А

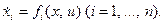
Согласно принципу максимума необходимым условием оптимальности управления и траектории 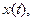т.е. обеспечения минимума функционала, бу­дет существование такой ненулевой вектор-функции 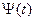при которой для лю­бого t, принадлежащего отрезку функция Н достигает в фиксированной точке максимума.

Для оптимизации функционала Z составим вспомогательную функцию типа функции Гамильтона

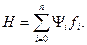
Здесь вспомогательная вектор-функция 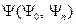определяется следующим образом:

Если удастся проинтегрировать систему, то решение получим в аналитической форме.

Рассмотрим геометрическую интерпретацию принципа максимума. Предположим, что необходимо перенести изображающую точку из начального положения в конечное 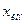(рис. 2.2.1) за минимальное время. Каждой точке фазового пространства, окружающего 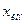, соответствуют определенная оптимальная траектория и отвечающее ей минимальное время перехода в эту точку. Вокруг 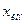построим поверхности, являющиеся геометрическим местом точек с одинаковым минимальным временем перехода в эту точку, т.е. изоповерхности или изохроны. Оптимальная по быстродействию траектория из в 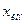должна быть предельно близка нормалям к изохронам настолько, насколько это позволяют ограничения, налагаемые на координаты. Действительно, всякое движение вдоль изохрон увеличивает время процесса без уменьшения отрезка времени, оставшегося до момента достижения 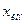. Математически условие оптимальности траектории означает, что на протяжении всей траектории скалярное произведение вектора скорости 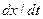на вектор, обратный градиенту времени перехода в конечную точку, должно быть максимально. Обозначим это произведение через Н, а вектор, обратный градиенту времени перехода, - через , т.е. Тогда это условие можно записать так:

где и 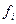– соответственно координаты векторов 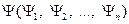и

Рис.2.2.1.Геометрическая интерпретация принципа максимума

Понтрягина.

Таким образом, условием оптимальности является максимум проекции вектора скорости 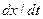на направление , что и составляет существо принципа максимума.

Принцип максимума дает лишь необходимое условие оптимальности, помогающее сузить класс управлений и траекторий, среди которых следует ис­кать оптимальные.

Date: 2016-07-18; view: 624; Нарушение авторских прав