
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейное программирование. Задача линейного программирования. Графическая иллюстрация. Симплекс-метод.
Численными методами математического программирования называют методы приближенного или точного решения задач нахождения экстремума целевой функции, основанные на построении конечной последовательности действий над конечным множеством чисел. Численные методы представляют собой последовательность однотипных шагов, или итераций.
Итерацией, называют регулярно повторяющийся в ходе реализации алгоритма состав процедур. В основе итерации лежат рекуррентные соотношения, определяющие новые значения каждой переменной через прежние значения ее и других переменных одной или нескольких предшествующих итерации. Итеративное представление алгоритма особенно эффективно при реализации его на ЭВМ, поскольку реализация различных итераций осуществляется одной и той же частью программы, что уменьшает затраты на программирование и сокращает объем необходимой памяти ЭВМ.
Численные методы подразделяются на конечные и бесконечные (итеративные). Конечные методы позволяют получать решение за конечное, обычно заранее неизвестное число шагов. Таким, например, является симплексный метод линейного программирования. В итеративных методах строится последовательность более точных приближений к решению. Процесс решения прекращается на том или ином числе итераций, когда достигается заданная точность решения.
Численные методы математического программирования получили чрезвычайно широкое применение в связи с развитием цифровой вычислительной техники.
Большинство задач оптимизации при проектировании систем управления относится к не линейным. Решение нелинейных задач - сложная вычислительная проблема, поэтому практически для решения используют приближенные методы, сущность которых состоит в том, что исходная постановка задачи сводится к одной линейной задаче или их совокупности. Основу многих процедур решения составляет линейное программирование.
1. Линейное программирование представляет собой численный метод решения задач нахождения экстремума линейной функции многих переменных при наличии линейных ограничений, т.е. линейных равенств или неравенств, связывающих эти переменные. Первые исследования по линейному программированию были проведены в З0-е годы в Ленинградском университете акад. Л.В.Канторовичем, Термин «линейное программирование» появился в 1951 г. в работах американских ученых Дж.Б.Данцига и Т.Купманса.
Математически задача линейного программирования ставится следующим образом: необходимо найти неотрицательные значения переменных  минимизирующие целевую функцию
минимизирующие целевую функцию

при наличии ограничений

Целевую функцию называют также линейной формой; а ограничения, представляющие систему линейно независимых уравнений, – системой ограничений.
На переменные  наложено ограничение неотрицательности, т. е.
наложено ограничение неотрицательности, т. е.  однако и таких решений имеется бесчисленное множество. Задача линейного программирования состоит в выборе из этого множества одного решения, которое обращает в минимум линейную форму.
однако и таких решений имеется бесчисленное множество. Задача линейного программирования состоит в выборе из этого множества одного решения, которое обращает в минимум линейную форму.
В ряде случаев все или некоторые ограничения задаются в виде неравенств
 или
или 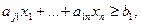 (2.3.1)
(2.3.1)
которые превращаются в равенства введением дополнительной переменной
При решении задач линейного программирования часто пользуются геометрическими интерпретациями.
Неравенства (2.3.1) определяют в пространстве  выпуклую область – выпуклый многогранник или многоугольник. Рассмотрим для простоты случай двух переменных:
выпуклую область – выпуклый многогранник или многоугольник. Рассмотрим для простоты случай двух переменных:  и
и  для которых справедлива система ограничений
для которых справедлива система ограничений

Каждое из этих соотношений определяет область, лежащую по одну сторону от прямой 
На рис. 2.3.1а заштрихована выпуклая область значений  и
и  . Линейная форма в случае двух переменных запишется в виде
. Линейная форма в случае двух переменных запишется в виде

Это уравнение прямой в плоскости 
 пересекающее оси
пересекающее оси  и
и  соответственно в точках
соответственно в точках  и
и  (рис. 2.3.16).
(рис. 2.3.16).
Величины  и
и  определяют угол наклона прямой а. Действительно,
определяют угол наклона прямой а. Действительно,

Расстояние от начала координат до прямой

Геометрически задача линейного программирования интерпретируется следующим образом. Если требуется найти такие  и
и  , которые придали бы линейной форме минимальное значение, то геометрически это означает, что необходимо провести прямую Z, проходящую хотя бы через одну точку области и имеющую минимальное расстояние d от начала координат. В случае нахождения максимума целевой функции это расстояние должно быть максимальным.
, которые придали бы линейной форме минимальное значение, то геометрически это означает, что необходимо провести прямую Z, проходящую хотя бы через одну точку области и имеющую минимальное расстояние d от начала координат. В случае нахождения максимума целевой функции это расстояние должно быть максимальным.
Симплексный метод, называемый также методом последовательного улучшения плана, так как решение задачи осуществляется итерациями. В геометрической интерпретации симплекс-метод состоит в переходе от одной вершины области допустимых значений к другой, соседней, в которой значение целевой функции лучше, чем в исходной точке. Движение происходит по периметру контура двумерной области, а для случая двух переменных - по ребрам многомерного многогранника.


Рис.2.3.1 Геометрическая интерпретация линейного программирования.
Пример. Завод выпускает два вида изделий  и
и  системы управления, используя для этой цели два вида технологических линеек
системы управления, используя для этой цели два вида технологических линеек  и
и 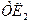 . На производство одного
. На производство одного  на
на  затрачивается 2 ч, а на
затрачивается 2 ч, а на 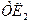 – 1 ч; на изготовление одного
– 1 ч; на изготовление одного  затрачивается соответственно 1 и 2 ч. Завод может использовать
затрачивается соответственно 1 и 2 ч. Завод может использовать  в течение 10, а
в течение 10, а 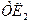 в течение 8 ч. Прибыль от реализации одного
в течение 8 ч. Прибыль от реализации одного  , составляет 5, а от реализации одного
, составляет 5, а от реализации одного  – 4 руб. Определить количество
– 4 руб. Определить количество  узлов
узлов  и количество
и количество  узлов
узлов  , которое необходимо выпустить заводу с тем, чтобы: 1) был полностью использован весь фонд времени двух технологических линеек; 2) завод получил максимальную прибыль.
, которое необходимо выпустить заводу с тем, чтобы: 1) был полностью использован весь фонд времени двух технологических линеек; 2) завод получил максимальную прибыль.
Решение. Целевую функцию запишем в виде

Ограничения имеют вид

| 
|

| 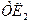
|
Для наглядности решим задачу геометрически. Отложим на осях координат  и
и  количество узлов (рис. 2.3.1). Здесь прямая / представляет производственные возможности
количество узлов (рис. 2.3.1). Здесь прямая / представляет производственные возможности  а прямая // –
а прямая // – 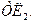 Заштрихованная область, ограниченная прямыми /, // и осями координат, дает представление о множестве допустимых планов, т. е. множестве значений
Заштрихованная область, ограниченная прямыми /, // и осями координат, дает представление о множестве допустимых планов, т. е. множестве значений  и
и  , удовлетворяющих ограничениям.
, удовлетворяющих ограничениям.
Целевая функция – прямая Z – передвигается параллельно самой себе по стрелке. Первая точка заштрихованной области, которой она коснется при таком перемещении, – точка К; она и будет решением задачи.
Таким образом, оптимальное решение всегда находится в точке пересечения граней многогранника ограничивающих условий. Если число ограничений больше двух, то это приведет к увеличению числа граней многоугольника (рис. 2.3.1). Для случая трех видов продукции (трехмерное пространство) геометрическая интерпретация задачи затруднена и вообще невозможна для n -мерного пространства (n >3).
2.2 Экспериментальное моделирование. Методы анализа и интерпретации результатов экспериментов. Корреляционный, регрессионный и дисперсионный анализ.
Возможность фиксации при моделировании системы S на ЭВМ значений переменных (параметров) и их статистическая обработка для получения интересующих экспериментатора характеристик позволяют провести объективный анализ связей между этими величинами. Для решения этой задачи существуют различные методы зависящие от целей исследования и вида получаемых при моделировании характеристик. Рассмотрим особенности использования методов корреляционного, регрессионного и дисперсионного анализа для результатов моделирования систем [4, 13, 34].
Корреляционный анализ результатов моделирования. С помощью корреляционного анализа исследователь может установить, насколько тесна связь между двумя (или более) случайными величинами, наблюдаемыми и фиксируемыми при моделировании конкретной системы S. Корреляционный анализ результатов моделирования сводится к оценке разброса значений  относительно среднего значения
относительно среднего значения  , т. е. к оценке силы корреляционной связи. Существование этих связей и их тесноту можно для схемы корреляционного анализа у = М[η/ζ=х] выразить при наличии линейной связи между исследуемыми величинами и нормальности их совместного распределения с помощью коэффициента корреляции
, т. е. к оценке силы корреляционной связи. Существование этих связей и их тесноту можно для схемы корреляционного анализа у = М[η/ζ=х] выразить при наличии линейной связи между исследуемыми величинами и нормальности их совместного распределения с помощью коэффициента корреляции

т. е. второй смешанный центральный момент делится на произведение средних квадратичных отклонений, чтобы иметь безразмерную величину, инвариантную относительно единиц измерения рассматриваемых случайных переменных.
Пример 7.1. Пусть результаты моделирования получены при N реализациях, а коэффициент корреляции

Очевидно, что данное соотношение требует минимальных затрат машинной памяти на обработку результатов моделирования. Получаемый при этом коэффициент корреляции  . При сделанных предположениях
. При сделанных предположениях  свидетельствует о взаимной независимости случайных переменных
свидетельствует о взаимной независимости случайных переменных  и
и  , исследуемых при моделировании (рис. 7.1, а). При
, исследуемых при моделировании (рис. 7.1, а). При  имеет место функциональная (т. е. нестохастическая) линейная зависимость вида у=b0+b1x, причем если
имеет место функциональная (т. е. нестохастическая) линейная зависимость вида у=b0+b1x, причем если  , то говорят о положительной корреляции, т. е. большие значения одной случайной величины соответствуют большим значениям другой (рис. 7.1, б). Случай
, то говорят о положительной корреляции, т. е. большие значения одной случайной величины соответствуют большим значениям другой (рис. 7.1, б). Случай 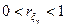 соответствует либо наличию линейной корреляции с рассеянием (рис. 7.1, в), либо наличию нелинейной корреляции результатов моделирования (рис. 7.1, г).
соответствует либо наличию линейной корреляции с рассеянием (рис. 7.1, в), либо наличию нелинейной корреляции результатов моделирования (рис. 7.1, г).

Рис. 7.1. Различные случаи корреляции переменных
Для того чтобы оценить точность полученной при обработке результатов моделирования системы S оценки  целесообразно ввести в рассмотрение коэффициент w = ln [(l+
целесообразно ввести в рассмотрение коэффициент w = ln [(l+  )/(l –
)/(l –  )]/2, причем w приближенно подчиняется гауссовскому распределению со средним значением и дисперсией:
)]/2, причем w приближенно подчиняется гауссовскому распределению со средним значением и дисперсией:
 ,
, 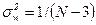 .
.
Из-за влияния числа реализаций при моделировании N на оценку коэффициента корреляции необходимо убедиться в том, что 0 <  ≤ 1 действительно отражает наличие статистически значимой корреляционной зависимости между исследуемыми переменными модели Мм. Это можно сделать проверкой гипотезы Н0:
≤ 1 действительно отражает наличие статистически значимой корреляционной зависимости между исследуемыми переменными модели Мм. Это можно сделать проверкой гипотезы Н0:  = 0. Если гипотеза Н0 при анализе отвергается, то корреляционную зависимость признают статистически значимой. Очевидно, что выборочное распределение введенного в рассмотрение коэффициента w при
= 0. Если гипотеза Н0 при анализе отвергается, то корреляционную зависимость признают статистически значимой. Очевидно, что выборочное распределение введенного в рассмотрение коэффициента w при  =0 является гауссовским с нулевым средним
=0 является гауссовским с нулевым средним  = 0и дисперсией
= 0и дисперсией  . Следовательно, область принятия гипотезы Н0 определяется неравенством
. Следовательно, область принятия гипотезы Н0 определяется неравенством
 ,
,
где zα/2 подчиняется нормированному гауссовскому распределению. Если  лежит вне приведенного интервала, то это означает наличие корреляционной зависимости между переменными модели на уровне значимости γ.
лежит вне приведенного интервала, то это означает наличие корреляционной зависимости между переменными модели на уровне значимости γ.
При анализе результатов моделирования системы S важно отметить то обстоятельство, что даже если удалось установить тесную зависимость между двумя переменными, то отсюда еще непосредственно не следует их причинно-следственная взаимообусловленность. Возможна ситуация, когда случайные ζ и η стохастически зависимы, хотя причинно они являются для системы S независимыми. При статистическом моделировании наличие такой зависимости может иметь место, например, из-за коррелированности последовательностей псевдослучайных чисел, используемых для имитации событий, положенных в основу вычисления значений х и у.
Таким образом, корреляционный анализ устанавливает связь между исследуемыми случайными переменными машинной модели
оценивает тесноту этой связи. Однако в дополнение к этому желательно располагать моделью зависимости, полученной после обработки результатов моделирования.
Регрессионный анализ результатов моделирования. Регрессионный анализ дает возможность построить модель, наилучшим образом соответствующую набору данных, полученных в ходе машинного эксперимента с системой S. Под наилучшим соответствием понимается минимизированная функция ошибки, являющаяся разностью между прогнозируемой моделью и данными эксперимента. Такой функцией ошибки при регрессионном анализе служит сумма квадратов ошибок.
Пример 7.2. Рассмотрим особенности регрессионного анализа результатов моделирования при построении линейной регрессионной модели. На рис. 7.2, а показаны точки  ,
,  ,
,  , полученные в машинном эксперименте с моделью Мм системы S.
, полученные в машинном эксперименте с моделью Мм системы S.
Делаем предположение, что модель результатов машинного эксперимента графически может быть представлена в виде прямой линии
 ,
,
где  — величина, предсказываемая регрессионной моделью.
— величина, предсказываемая регрессионной моделью.
Требуется получить такие значения коэффициентов  и
и  при которых сумма квадратов ошибок является минимальной. На рисунке ошибка
при которых сумма квадратов ошибок является минимальной. На рисунке ошибка  ,
,  для каждой экспериментальной точки определяется как расстояние по вертикали от этой точки до линии регрессии у=φ(х).
для каждой экспериментальной точки определяется как расстояние по вертикали от этой точки до линии регрессии у=φ(х).

Рис. 7.2. Построение линейной регрессионной модели
Обозначим  ,
,  . Тогда выражение для ошибок будет иметь вид
. Тогда выражение для ошибок будет иметь вид
 , а функция ошибки
, а функция ошибки  .
.
Для получения  и
и  , при которых функция F0 является минимальной, применяются обычные методы математического анализа. Условием минимума является
, при которых функция F0 является минимальной, применяются обычные методы математического анализа. Условием минимума является  ;
;  .
.
Дифференцируя  , получаем
, получаем
 ,
,
 .
.
Решая систему этих двух линейных алгебраических уравнений, можно получить значения  и
и  . В матричном представлении эти уравнения имеют вид
. В матричном представлении эти уравнения имеют вид



Решая это уравнение, получаем
 ,
,
 ,
,
где N — число реализаций при моделировании системы.
Соотношения для вычисления  и
и  , требуют минимального объема памяти ЭВМ для обработки результатов моделирования. Обычно мерой ошибки регрессионной модели служит среднее квадратичное отклонение
, требуют минимального объема памяти ЭВМ для обработки результатов моделирования. Обычно мерой ошибки регрессионной модели служит среднее квадратичное отклонение
 .
.
Для нормально распределенных процессов приблизительно 67% точек находится в пределах одного отклонения σе от линии регрессии и 95% — в пределах 2σе (трубки А и В соответственно на рис. 7.2, б). Дая проверки точности оценок  и
и  , регрессионной модели могут быть использованы, например, критерии Фишера (F-распределение) и Стьюдента (t-распределение). Аналогично могут быть оценены коэффициенты уравнения регрессии и для случая нелинейной аппроксимации.
, регрессионной модели могут быть использованы, например, критерии Фишера (F-распределение) и Стьюдента (t-распределение). Аналогично могут быть оценены коэффициенты уравнения регрессии и для случая нелинейной аппроксимации.
Дисперсионный анализ результатов моделирования. При обработке и анализе результатов моделирования часто возникает задача сравнения средних выборок. Если в результате такой проверки окажется, что математическое ожидание совокупностей случайных переменных {у(1)}, {у(2)},..., {у(n)} отличается незначительно, то статистический материал, полученный в результате моделирования, можно считать однородным (в случае равенства двух первых моментов). Это дает возможность объединить все совокупности в одну и позволяет существенно увеличить информацию о свойствах исследуемой модели Мм, а следовательно, и системы S. Попарное использование для этих целей критериев Смирнова и Стьюдента для проверки нулевой гипотезы затруднено в связи с наличием большого числа выборок при моделировании системы. Поэтому для этой цели используется дисперсионный анализ.
Пример 7.3. Рассмотрим решение задачи дисперсионного анализа при обработке результатов моделирования системны в следующей постановке. Пусть генеральные совокупности случайной величины {у(1)}, {у(2)},..., {у(n)} имеют нормальное распределение и одинаковую дисперсию. Необходимо по выборочным средним значениям при некотором уровне значимости у проверить нулевую гипотезу Н0 о равенстве математических ожиданий. Выявим влияние на результаты моделирования только одного фактора, т. е. рассмотрим однофакторный дисперсионный анализ.
Допустим, изучаемый фактор х привел к выборке значений неслучайной величины У следующего вида: у1, у2,..., уk где к — количество уровней фактора х. Влияние фактора будем оценивать неслучайной величиной Dх, называемой факторной дисперсией:
 ,
,
где  — среднее арифметическое значение величины Y.
— среднее арифметическое значение величины Y.
Если генеральная дисперсия D[у] известна, то для оценки случайности разброса наблюдений необходимо сравнить D[y] с выборочной дисперсией  , используя критерий Фишера (F-распределение). Если эмпирическое значение FЭ попадает в критическую область, то влияние фактора х считается значимым, а разброс значений х — неслучайным. Если генеральная дисперсия D[х] до проведения машинного эксперимента с моделью Мм неизвестна, то необходимо при моделировании найти ее оценку.
, используя критерий Фишера (F-распределение). Если эмпирическое значение FЭ попадает в критическую область, то влияние фактора х считается значимым, а разброс значений х — неслучайным. Если генеральная дисперсия D[х] до проведения машинного эксперимента с моделью Мм неизвестна, то необходимо при моделировании найти ее оценку.
Пусть серия наблюдений на уровне уi, имеет вид уi1, у i2,...,yin, где n число повторных наблюдений на i -м уровне. Тогда на i -м уровне среднее значение наблюдений
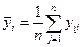 ,
,
среднее значение наблюдений по всем уровням
 .
.
Общая выборочная дисперсия всех наблюдений
 .
.
При этом разброс значений у определяется суммарным влиянием случайных причин и фактора х. Задача дисперсионного анализа состоит в том, чтобы разложить общую дисперсию D [у] на составляющие, связанные со случайными и неслучайными причинами.
Оценка генеральной дисперсия, связанной со случайными факторами,
 ,
,
а оценка факторной дисперсии
 .
.
Учитывая, что факторная дисперсия наиболее заметна при анализе средних значений на i -м уровне фактора, а остаточная дисперсия (дисперсия случайности) для средних значений в n раз меньше, чем для отдельных измерений, найдем более точную оценку выборочной дисперсии:
 .
.
Умножив обе части этого выражения на n, получим в правой части выборочную дисперсию  , имеющую (k - 1)-ю степень свободы. Влияние фактора х будет значимым, если при заданном γ выполняется неравенство
, имеющую (k - 1)-ю степень свободы. Влияние фактора х будет значимым, если при заданном γ выполняется неравенство 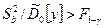 . В противном случае влиянием фактора х на результаты моделирования можно пренебречь и считать нулевую гипотезу Н0 о равенстве средних значений на различных уровнях справедливой.
. В противном случае влиянием фактора х на результаты моделирования можно пренебречь и считать нулевую гипотезу Н0 о равенстве средних значений на различных уровнях справедливой.
Таким образом, дисперсионный анализ позволяет вместо проверки нулевой гипотезы о равенстве средних значений выборок проводить при обработке результатов моделирования проверку нулевой гипотезы о тождественности выборочной и генеральной дисперсий.
Возможны и другие подходы к анализу и интерпретации результатов моделирования, но при этом необходимо помнить, что их эффективность существенно зависит от вида и свойств конкретной моделируемой системы S.
Теория планирования экспериментов. Понятие факторов и факторного пространства. Полно- и дробнофакторные эксперименты. Виды функций отклика и определение ее коэффициентов. Статистический анализ результатов
Под научным планированием экспериментов понимают математическое установление оптимального плана их проведения.
Основным требованием при организации любого эксперимента является минимизация времени и числа испытании при сохранении требуемой достоверности результатов. Форма представления результатов должна быть удобна для последующих расчетов, как обычных, так и вероятностных. Последнее накладывает особый отпечаток на проведение испытаний. Если ранее в эксперименте можно было ограничиваться определением только средних значений исследуемой величины, то с внедрением вероятностных методов расчета значительное место в эксперименте уделяется изучению рассеяния и оценке достоверности полученных результатов. Увеличивается удельный вес многофакторных испытаний, т.е. испытаний, учитывающих влияние многих факторов. Эксперимент становится сложнее и дороже. Это стимулирует поиск оптимального плана проведения испытаний.

Рисунок 1. Схематизация эксперимента.
Вопрос оптимальности плана неразрывно связан с методом обработки результатов испытаний и решается в рамках научного планирования эксперимента — нового направления в математической статистике и теории вероятностей.
Резкое сокращение числа испытаний при их научном планировании достигается за счет использования известных или предполагаемых математических зависимостей (в частности, вида искомой функции), возможности планировать эксперимент с учетом уже полученных результатов и главное, за счет целенаправленного одновременного варьирования изучаемых факторов. Последнее является отличительной чертой активного эксперимента от пассивного, т.е. эксперимента, который «ведет природа», и, следовательно, значения факторов не зависят от экспериментатора. Эффективность планирования тем выше, чем сложнее изучаемый объект.
Используя кибернетический подход, объект исследования рассматривают как систему («черный ящик») рисунок 1, у которой известны входной и выходной параметры, но не известно внутреннее устройство. Входные параметры называют факторами, выходной параметр — откликом. Факторы рассматривают как детерминированные величины  , отклик — как случайную величину Y. Обычно полагают, что закон распределения Y известен из теоретических соображений или экспериментальных исследований.
, отклик — как случайную величину Y. Обычно полагают, что закон распределения Y известен из теоретических соображений или экспериментальных исследований.
Уравнение связывающее отклик с факторами  , называют функцией отклика.
, называют функцией отклика.
Цель эксперимента состоит в оценке наиболее простым способом функции отклика. В такой постановке эксперимент называют интерполяционным, основанным на интерполяции – нахождении функции по некоторым её значениям.
Более сложным является экстремальный эксперимент, предназначенный для определения оптимума. Критерий оптимальности формулируется исследователем. Например, оптимальность условий протекания металлургических процессов в смысле достижения наибольшей прочности материалов, или оптимальные условия резания, минимизирующие себестоимость изделия.
В математическом смысле целью экстремальных экспериментов является поиск экстремума функции отклика.
При экспериментальных исследованиях работоспособности и надежности деталей машин наиболее распространен интерполяционный эксперимент. Характерная область применения — изучение влияния определенных факторов (погруженности, концентрации напряжений, масштабного фактора, шероховатости поверхности и т.д.) на долговечность или на предельные по критерию прочности напряжения деталей.
Примерами экстремальных экспериментов в области деталей машин могут служить: оптимизация состава антифрикционных сплавов и покрытий, металлокерамических материалов, пластмасс для отдельных групп деталей машин.
Вид функции отклика (линейная, степенная, логарифмическая и т.д.) или математическую модель объекта исследования устанавливают, исходя из физических представлений о самом объектеили на основе опыта предыдущих исследований.
При отсутствии таких сведений функцию отклика представляют результатом ее разложения в ряд Тейлора т.е. используют модель в виде полинома. В простейшем случае выбирают полином первого порядка, линейный по всем переменным

где  и
и  — коэффициенты функции.
— коэффициенты функции.
Функция отклика несколько усложняется, если необходимо учитывать взаимодействие факторов
 .
.
Для описания области, близкой к оптимуму, выбирают полином второго порядка
 .
.
Использование полиномов выше второго порядка встречается довольно редко.
Для тех же полиномиальных зависимостей, но найденных на основе экспериментов вместо величины  , вводится оценка её среднего значения
, вводится оценка её среднего значения  соответственно вместо коэффициентов
соответственно вместо коэффициентов  ,
,  ,
,  ,
,  — их оценка,
— их оценка,  ,
,  ,
,  ,
,  .Например, при оценке функции отклика (эмпирического уравнения регрессии) в виде полинома второго порядка имеем
.Например, при оценке функции отклика (эмпирического уравнения регрессии) в виде полинома второго порядка имеем
 .
.
Коэффициенты полинома (коэффициенты регрессии) соответствуют частным производным в точке, вокруг которой функция отклика разлагается в ряд Тейлора. Если при выборе модели у исследователя нет оснований отдать предпочтение одной из трех указанных выше функций, то начинать надо с простейшей — линейной функции. По результатам испытаний проверяют адекватность модели, т.е. её соответствие реальности. В случае отрицательного результата переходят к более сложной модели, например, к модели, учитывающей взаимодействие факторов. Желательно, чтобы при таком переходе ранее выполненные испытания полностью учитывались при составлении нового плана эксперимента, т.е. чтобы план был композиционным.
Факторы, подлежащие исследованию, обусловлены целью эксперимента. Однако надо учитывать, что на отклик (выходной параметр) оказывает влияние довольно большое число других факторов среди которых есть и неуправляемые.
В процессе экспериментов исследуемые факторы варьируют, а остальные поддерживают на постоянном уровне. Чтобы исключить влияние неуправляемых факторов, им задают среднее значение или их рандомизируют, т.е. делают случайными. Рандомизация усредняет по всем опытам действие неуправляемых факторов.
Наиболее простой способ рандомизации — случайная последовательность проведения всех опытов.
Значения (уровни) факторов удобно задавать в относительных (кодированных) величинах. Максимальный уровень фактора равен +1, минимальный –1 и средний 0. В общем случае относительное или кодированное значение фактора равно

где  ,
,  — максимальное и минимальное абсолютные значения фактора, т.е. пределы варьирования фактора в эксперименте; X — абсолютное значение фактора.
— максимальное и минимальное абсолютные значения фактора, т.е. пределы варьирования фактора в эксперименте; X — абсолютное значение фактора.
Для качественных факторов (марка стали, вид термообработки, качество покрытий и т.д.) строят условные порядковые шкалы, устанавливающие соответствие уровней качественных показателей числам натурального ряда, т.е. производят кодирование. Например, для качественного фактора, учитывающего наличие в эксперименте сталей двух плавок, назначают два уровня: один, равный +1 (сталь первой плавки), второй –1 (сталь второй плавки). В дальнейшем с ним поступают так же, как и с количественным фактором.
К исследуемым факторам предъявляют следующие требования:
- управляемость – возможность установления и поддержания фактора на выбранных уровнях;
- независимость – возможность устанавливать фактор на выбранном уровне вне зависимости от уровней других факторов;
- совместимость – все комбинации факторов осуществимы и безопасны.
Планирование эксперимента в основном сводится к выбору числа уровней факторов и определению значения (уровня) каждого фактора в опыте.
Выбранное число уровней p в сочетании с числом факторов k определяют число возможных опытов N, которое равно N=pk. Если каждый опыт повторяется m раз, то число образцов соответственно равно mN. Число повторении m может быть выбрано по таблицам на основе задания допустимой ошибки и доверительной вероятности.
Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называют полным факторным экспериментом (ПФЭ).
Для линейной модели достаточно варьирование факторов на двух уровнях. В этом случае имеем ПФЭ типа 2 k.
Графически план такого эксперимента для двух факторов можно представить в координатах кодированных значений факторов x1 и x2 (рисунок 2).

Рисунок 2. План полного двух факторного эксперимента.

Рисунок 3.План полного трёх факторного эксперимента.
Условия проведения опытов соответствуют вершинам квадрата. Для первого опыта 
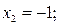 второго
второго 
 третьего
третьего 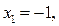
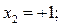 четвертого
четвертого 
 Отметим, что номера опытов нами назначены произвольно.
Отметим, что номера опытов нами назначены произвольно.
План эксперимента можно задавать таблицей, называемой матрицей плана. Матрица плана ПФЭ типа 22 представлена в таблице 1. В таблице и в дальнейшем применяем сокращенное обозначение уровней факторов: вместо +1 и –1 обозначаем + и –.
Таблица 1
| № опыта | Факторы | № опыта | Факторы | ||
| x1 | x2 | x1 | x2 | ||
| + + | – + | – – | + – |
Более исчерпывающая информация об эксперименте представляется матрицей планирования эксперимента. Для ПФЭ типа 22 матрица планирования представлена в таблице 2 и включает матрицу плана эксперимента, значения фиктивного фактора x0, эффект взаимодействия факторов x1 x2 (при необходимости его учета) и значения отклика.
Таблица 2.
| № опыта | Факторы | Эффект взаимодействия | Отклик | |||
| x1 | x2 | x3 | x1 x2 | Повторы | Среднее значение | |
| + + + + | + + – – | – + + – | – + – + | y11,y12, … y21,y22, … y31,y32, … y41,y42, … | 



|
Матрица плана трехфакторного эксперимента (в таблице 3 заключена в пунктирную рамку) образуется от матрицы плана двухфакторного эксперимента, повторенного дважды: одни раз — при нижнем уровне, а второй раз — при верхнем уровне третьего фактора.
Графически (рисунок 3) план полного факторного эксперимента типа можно представить вершинами куба, построенного в координатах кодированных значении факторов.
Матрица планирования для трехфакторного эксперимента, функция отклика которого соответствует полиному второго порядка, представлена в таблице 3.
Таблица 3.
| № опыта | Факторы | Эффекты взаимодействия | Отклик | |||||||
| x1 | x2 | x3 | x4 | x1 x2 | x1 x3 | x2 x3 | x1x2x3 | Повторы | Среднее значение | |
| + + + + + + + + | + + – – + + – – | – + + – – + + – | – – – – + + + + | – + – + – + – + | – – + + + + – – | + – – + – + + – | + – + – – + – + | y11,y12, … y21,y22, … y31,y32, … y41,y42, … y51,y52, … y61,y62, … y71,y72, … y81,y82, … | 




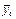


|
Основные свойства планов полного факторного эксперимента типа 2 k следующие.
1. Симметричность плана относительно центра эксперимента (начала координат кодированных переменных) выражается равенством нулю сумм кодированных значений i -го (i = 1,2,…k) фактора по всем опытам, т.е. 
2. Условия нормировки, означающие, что ПФЭ предусмотрено два уровня +1 и –1, т. е. 
3. Ортогональность плана предполагает равенство, нулю суммы попарно переменных факторов  и
и  , т.е. i –го и j –го факторов в u –м
, т.е. i –го и j –го факторов в u –м  где i ≠ j; i, j =0,1,2,… k.
где i ≠ j; i, j =0,1,2,… k.
4. Ротатабельность — точность предсказания значений выходного параметра одинакова на равных расстояниях от центра эксперимента.
Для линейной модели число коэффициентов, подлежащих определению равно числу факторов k плюс единица (свободный член). Если учесть, что число опытов ПФЭ равно 2 k, то очевидна большая избыточность опытов. В этом случае пользуются дробным факторным экспериментам (ДФЭ), эффективность которого увеличивается с ростом числа факторов k. Основа построения ДФЭ — замена в матрице планирования наиболее слабого эффекта взаимодействия (произведения факторов) новым фактором. Какой из эффектов взаимодействия наиболее слабый, т.е. менее всего влияет на величину выходного параметра, решает экспериментатор на основании физических представлений об исследуемом объекте. Например, планируя ДФЭ для трех факторов, используют матрицу планирования двухфакторного эксперимента, где эффект взаимодействия x 1 x 2 заменяют фактором x3 (таблица 4). Однако в ДФЭ оценки коэффициентов функции отклика не будут раздельными. Из таблицы 4 видно, что столбцы для x1 и x2,x3 одинаковы, следовательно, оценка коэффициента β 1 обозначаемая через b 1 смешана с коэффициентами β 1 и β 23, т.е. b 1→ β 1+ β 23.
Аналогично находим смешение для оценок b 2 и b 3: b 2 → β 2+ β 13; b 3 → β 3+ β 12.
Отметим, что смешение оценок не отразится на результатах, если проверка адекватности подтвердит правомерность выбора линейной модели, следовательно, возможность пренебрежения эффектами взаимодействия.
В силу ортогональности матриц планирования эксперимента формулы для определения оценок b 0, b i и b ij неизвестных коэффициентов β 0, β i, β ij функции отклика (полинома первого порядка) предельно просты:



где xiu xju — величина i-го и j -го факторов (i  j; i, j =1,2,…, k) в u -м опыте.
j; i, j =1,2,…, k) в u -м опыте.
Таблица 4.
| № опыта | Матрица плана ДФЭ | Эффекты взаимодействия | ||||
| x1 | x2, | x3 | x1x2 | x1x3 | x2x3 | |
| + + – – | – + + – | – + – + | – + – + | – + + – | + + – – |
Среднее значение отклика  в u -м опыте определяется по формуле
в u -м опыте определяется по формуле

где m — число повторов опыта; yuq — текущее значение отклика в u -м опыте при q-м повторе.
Для квадратичных моделей, когда функция отклика описывается полиномом второго порядка, необходимо увеличить число уровней фактора до трех. Полный факторный эксперимент на трех уровнях предусматривает проведение N=3k опытов (k — число факторов), что намного больше, чем число неизвестных коэффициентов модели. Существенное сокращение числа опытов получают в композиционных планах, ядром которых являются планы линейных моделей. К плану ПФЭ типа 2k добавляют опыты в центре эксперимента (нулевые точки) и на расстоянии α от центра («звездные» точки). Таким образом, по оси координат каждого фактора получают пять значений (уровней): –α, –1, 0, +1, + α. Длина «плеча» α и число опытов в центре плана зависят от требований, предъявляемых к плану. Требование ортогональности приводит к ортогональным центральным композиционным планам (ОЦКП); требование ротатабельности — к ротатабельным центральным композиционным планам (РЦКП). В случае, когда по чисто техническим причинам значения фактора не могут выходить за пределы заданной области эксперимента, т. е.  , применяют композиционные планы типа bm, в которых α равно единице.
, применяют композиционные планы типа bm, в которых α равно единице.

Рисунок 4. План двухфакторного эксперимента для
целевой функции нелинейной модели
Для ортогонального центрального композиционного плана (рассмотрением которого мы ограничиваемся) число опытов в центре равно единице, а величину плеча α выбирают в зависимости от числа факторов k. Так при k равном 2; 3; 4; 5, значения плеча соответственно выбирают 1; 1,215; 1,414; 1,547.
Для двух факторов план ОЦКП эксперимента представлен матрицей в таблице 5 и графически на рисунке 4, где вершины квадрата в координатах кодированных значений x1 и x2 обозначают опыты плана ПФЭ типа 2 k или ядро плана, к которому добавлена нулевая точка (центр плана) и четыре «звёздных». расположенных на середине сторон квадрата. Номера опытов на рисунке 4 соответствуют номерам строк таблице. 5.
Для трех факторов план ОЦКП эксперимента, составленный аналогично двухфакторному, приведен в таблице 6. Геометрически план может быть представлен кубом, вершины которого соответствуют опытам ПФЭ типа 2 k, к которым добавляют шесть «звездных» точек, расположенных на расстоянии α от середины ребер куба и одну нулевую точку в центре куба.
Таблица 5.
| № опыта | Факторы | Примечания | |
| x1 | x2 | ||
| + + – – | – + + – | Ядро плана | |
| + – | – + | «Звёздные» точки | |
| Нулевая точка |
Таблица 6.
| № опыта | Факторы | Примечания | ||
| x1 | x2 | x3 | ||
| + + – – + + – – | – + + – – + + – | – – – – + + + + | Ядро плана | |
| – 1,215 + 1,215 | – 1,215 + 1,215 | – 1,215 + 1,215 | «Звёздные» точки | |
| Нулевая точка |
Оценки b0, bi, bij, bii (i =1,2,..., k; i≠j) неизвестных коэффициентов функции отклика (полинома второго порядка) β0, βi, βij, βii определяют по следующим зависимостям:




где  при любом i =1,2,…, k.
при любом i =1,2,…, k.
В экстремальных экспериментах поиск оптимума поочередным варьированием переменных требует проведения очень большого количества опытов. Поэтому целесообразно применять метод крутого восхождения, который заключается в следующем. Для некоторой начальной точки поверхности отклика ставят интерполяционный эксперимент. Число опытов невелико и достаточно для описания небольшого участка поверхности отклика полиномом первого порядка. Вектор-градиент этого полинома (функции отклика) определяет направление наиболее короткого (крутого) пути к экстремуму. Составляющие градиент являются частными производными функции отклика по факторам.
Движение по поверхности отклика в направлении градиента начинают от начальной точки. Шаг движения или изменения значений фактора при переходе к следующему опыту устанавливают в зависимости от степени влияния фактора на отклик. Значение отклика, называемого в экстремальных экспериментах критерием оптимизации или целевой функцией, изменяется от опыта к опыту. Совпадение или незначительное отличие результатов двух соседних опытов означает достижение области, близкой к стационарной. В этой области ставят заключительный интерполяционный эксперимент с высокой концентрацией опытов.
Статистический анализ результатов испытаний необходим для оценки достоверности эксперимента и включает следующие этапы.
1. Проверка воспроизводимости или постоянства дисперсии отклика. Сводится к проверке гипотезы об однородности дисперсий 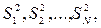 найденных по результатам N опытов.
найденных по результатам N опытов.
Дисперсия отклика  для u -го опыта равна
для u -го опыта равна
 u =1,2,…, N,
u =1,2,…, N,
где uuq — отклик u -го опыта при q -м повторе, m — число повторов опыта.
Вычисляем экспериментальное значение критерия Кохрена, т.е. отношение максимальной  из N дисперсии к сумме всех дисперсий
из N дисперсии к сумме всех дисперсий

Гипотеза об однородности дисперсий подтверждается, если вычисленное значение критерия не превышает критического значения, определенного по соответствующим таблицам, в зависимости от числа степеней свободы k1=m—1, k2=N и доверительной вероятности Рдов.
Критерий Кохрена применяют при одинаковом для каждого опыта числе повторов. В более общем случае используют критерий Бартлета.
2. Адекватность модели, т.е. пригодность ранее принятой функции отклика для описания реального объекта исследования, проверяют по отношению дисперсий адекватности и воспроизводимости.
Дисперсию воспроизводимости или оценку дисперсии отклика определяем по формуле

Дисперсию адекватности определяем по формуле

где k — число факторов;  — расчетная оценка среднего значения отклика в u –м опыте, вычисляемая по соответствующему полиному. Например, для линейной модели
— расчетная оценка среднего значения отклика в u –м опыте, вычисляемая по соответствующему полиному. Например, для линейной модели
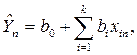
где xiu — значение i-го фактора в u–м опыте.
Экспериментальное значение F–критерия (критерия Фишера) равно

Модель считают адекватной, если вычисленное значение F меньше критического, определенного по таблицам F–распределения [5, 45], в зависимости от числа степенен свободы k1=N–(k+1), k2=(m–1)N и доверительной вероятности Рдов.
Для насыщенных планов, в которых число определяемых коэффициентов равно числу опытов, для проверки адекватности проводят дополнительные опыты. Так, для линейной модели дополнительно ставят опыты в центре плана. По расхождению между полученным и расчетным значениями отклика принимают решения об адекватности модели.
При неадекватности модели возможны следующие действия: усложнение модели, достройка плана, преобразование переменных, изменение интервалов варьирования.
3. Значимость коэффициентов модели проверяем по i–критерию Стьюдента. Проверку начинаем с вычисления дисперсий коэффициентов.
Для планов дробного и полного факторного эксперимента типа 2k дисперсии оценок коэффициентов b0, bi, bij одинаковы и определяются по формуле
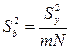
Экспериментальное значение критерия Стьюдента равно

где │b│ — абсолютное значение оценки проверяемого коэффициента, т.е. одного из коэффициентов b0, bi, bij.
Коэффициент считают значимым, если вычисленное значение критерия больше, чем критическое значение, выбираемое по таблицам распределения Стьюдента, в зависимости от числа степеней свободы k=(m–1)N и доверительной вероятности Рдов.
Для квадратичной модели, когда испытания проводят по ортогональному центральному плану, дисперсии оценок коэффициентов модели определяют по следующим зависимостям:




где  — общая дисперсия среднего значения отклика определятся по формуле
— общая дисперсия среднего значения отклика определятся по формуле

Далее для каждого из коэффициентов вычисляют i–критерий Стьюдента (отношение абсолютного значения коэффициента к его среднему квадратическому отклонению) и сравнивают с табличным значением, найденным в зависимости от числа степеней свободы k=(m–1)N и доверительной вероятности Рдов.
Пример. Исследовать влияние радиального Δ и углового  смещений осей соединяемых валов на долговечность муфты с резиновым торообразным элементом вогнутого профиля. Муфта нагружена номинальным моментом T =100 Н·м, наружный диаметр муфты D0 =165 мм.
смещений осей соединяемых валов на долговечность муфты с резиновым торообразным элементом вогнутого профиля. Муфта нагружена номинальным моментом T =100 Н·м, наружный диаметр муфты D0 =165 мм.
Решение. Схематизация эксперимента. На муфту (объект исследования) действуют два фактора: радиальное Δ и угловое  смещения полумуфт. Кодированные значения факторов обозначаем соответственно через х1, х2 и определяем по следующим зависимостям:
смещения полумуфт. Кодированные значения факторов обозначаем соответственно через х1, х2 и определяем по следующим зависимостям:


Предельные значения радиальных и угловых смещении устанавливаем, исходя из опыта эксплуатации муфт:  = 5 мм;
= 5 мм; 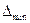 = 3 мм;
= 3 мм;  =
=  ;
; 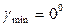 . Подставляя предельные значения в формулы для x1 и x2, получаем
. Подставляя предельные значения в формулы для x1 и x2, получаем

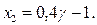
В качестве отклика У рассматриваем логарифмы ресурса lgL где L –ресурс, выраженный в оборотах муфты.
Требуется оценить функцию отклика, т.е. найти связь между факторами и откликом.
Функцию отклика задаем полиномом первого порядка с учетом эффекта взаимодействия

где β0, β1, β2, β12 – коэффициенты функции.
Соответственно оценку функций отклика (эмпирического уравнения регрессии) ищем в виде

где b0, b1, b2, b12. – оценки коэффициентов β0, β1, β2, β12 соответственно.
При планировании эксперимента выбран план полного факторного эксперимента типа 22. Число опытов N =4; число повторов каждого опыта m =3; необходимое число образцов равно mN =12.
Испытания проводили на стенде с замкнутым контуром, спроектированном и изготовленном в МВТУ им. Н.Э. Баумана. Циркулирующий в контуре момент соответствовал номинальному моменту испытуемой муфты. Конструкция стенда позволяет изменять радиальное и угловое смещение полумуфт в широких пределах.
Результаты испытаний на долговечность представлены в виде значений логарифмов ресурса (см. матрицу планирования эксперимента, столбец «Повторы», таблица 7).
Таблица 7.
Date: 2016-07-18; view: 773; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |