Дифференциал. Его основные свойства

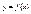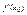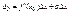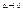Пусть ф-ция имеет в точке x₀ конечную производную . Тогда , где при 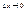. Т.е если Dx считать беск. малой, то оба слагаемые будут беск. малыми. Сравним их с величиной Dy, при условии, что .

,

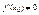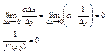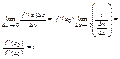
a×Dx– беск. малая более высокого порядка по сравнению с Dy, а f’(x₀)Dx эквивалентно Dy. Слагаемое f’(x₀)Dx получило название дифференциала функции f’(x₀)Dx=dy. Дифференциалом функции в некоторой точке называется произведение производной функции в этой точке на приращение независимой переменной:

.

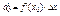К понятию дифференциала можно подойти через определение производной:

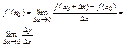
беск. малые Dy и Dx одного порядка, а беск. малая f’(x₀)Dx представляет главную линейную часть беск. малой Dy. Поэтому дифференциал – главная линейная часть приращения Dy. Понятие дифф-ла в некоторой точке связано с сущ-м производной в этой точке. Т.к. Dx м. брать произвольно, независимо от x, то значение диф-ла dy так же будет меняться, оставаясь пропорц-м Dx. Т.обр., диф-л функции есть некоторая часть приращения функции, линейно зависящая от приращения аргумента Dx: dy=ADx. Диф-л ф-ции линейно выражается через Dx, в то время как приращение функции Dy находится в более сложной зависимости от Dx. Для решения задач на приближенное нахождение знач. функции м. получить общую формулу. Пусть y=f(x) ф-ция, имеющая производную f’(x) в точке x₀. Тогда если x-x₀=Dx, то Dy=f(x)-f(x₀) и dy=f’(x₀)(x-x₀) т.к. Dy»dy, то f(x)-f(x₀)»f’(x₀)(x-x₀), т.е. f(x)»f(x₀)+f’(x₀)(x-x₀). Эта формула позволяет приближ-но заменять произвольную ф-цию, имеющую производную, линейной ф-цией. При этом точность при такой замене тем большая, чем ближе x к x₀. Геометрически эта замена означает, что участок кривой f(x) в окрестности точки [x₀,f(x₀)] заменяется отрезком касательной к кривой в этой точке:y-y₀=k(x-x₀), где y₀=f(x₀), а k=f¢(x₀) угловой коэффициент касательной. Геометрический смысл дифференциала: диф-л функции геометрически представляет собой приращение ординаты касательной, в то время как приращение функции Dy есть приращение ординаты самой кривой y=f(x). Диф-л м.б. меньше, больше или равен приращению функции. Равен, например, в случае когда ф-ия линейная. Механический смысл: пусть y=f(x) закон прямолинейного движения. Тогда y=f’(x)– скорость движения в момент x, а диф-л путь, который прошло бы тело за время Dx, если бы оно двигалось равномерно со скоростью, равной скорости в момент времени x. Если функция совпадает с независимой переменной, то ее приращение и диф-л равны между собой. В связи с этим будем считать диф-л по определению равным приращению этой переменной: dx=Dx. Тогда приращение функции можно представить как: dy=f’(x)dx. Отсюда f’(x)=dy/dx, т.е производная функции равна частному от деления диф-ла ф-ции на диф-л аргумента. Отношение dy/dx будет постоянным, равным f’(x), т.к. dy изменяется пропорционально dx, несмотря на то, что dx можно брать произвольно. Чтобы найти диф-л некоторой ф-ции, достаточно вычислить ее производную и затем умножить на диф-л аргумента. Формулы для отыскания производных легко преобразуются ф формулы для отыскания диф-лов: d(c)=0×dx=0, d(x^k)=kx^k-1, d(a^x)=a^xlnadx ит.д. Правила дифф-ния: d(cu)=cdu, т.к. d(cu)=(cu)’dx=c(u’dx)=cdu,

,

,

.

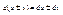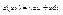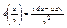Диф-л от диф-ла ф-ции y=f(x) в некоторой точке наз-я диф-лом второго порядка в этой точке и обозначается d(dy)=d²y. Диф-л от диф-ла n-го порядка наз-ся диф-лом n порядка: dⁿy. dⁿy=y⁽ⁿ⁾dxⁿ и

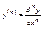
Инвариантность: y=f(x), x=j(t)Þy=f(j(t)), y’_t=y’_xx’_t, dy=y’_tdt, заменяя dy=y’_xx’_tdt=y’_xdx, т.обр. вернулись к прежней форме диф-ла. Форма диф-ла м.б. сохранена даже если прежняя независимая переменная заменена новой. Это св-во называют инвариантностью диф-ла.