Признаки сходимости и расходимости числовых рядов

Положительные ряды.

Опр: Полож. Р. наз. р, все члены кот. не отриц.

Необх. и достат. признак сход. полож. р.

Пусть дан полож. Р. (1):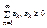

Т: для того, чтобы полож. Р. (1) сход., необх. и дост., чтобы последовательность его частичных сумм была ограничена сверху.

Док-во:

Необх: Пусть ряд (1) сход, тогда по определению сход-и ряда сущ. кон-й предел, limSn(n®¥)=S, тогда послед-ть (S_n) част-х сумм ряда ограничена, как всякая сходящаяся послед.

Достаточность: Пусть послед (S_n) частичных сумм ряда огр. сверху. Т.к. члены ряда неотриц., то .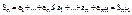

Так как (S_n) - монотонно возраст. послед., а т.к. она огр. сверху, то она имеет предел (конечный), следоват-о р. сход.

Дост-е признаки сход. полож. р.

Т1: пусть даны два полож. ряда: (1) 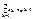и (2) 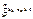, причем 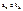, к = 1,2,…, тогда

a) Если р. (2) - сход, то и (1) - сход.

b) Если р. (1) - расход, то и (2) - расход.

(Из сход. ряда с большими чл => сход. р. с меньшими чл. Из расход. р. с меньшими чл. => расход. р. с большими чл.).

Док-во: а) Пусть (2) - сход. Тогда по необх. и дост. призн. сход р.: $-ет М, "n: 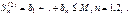тогда 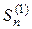ограничена сверху. Значит р. (1) - сход.

б) (1) - расход. Док, что и ряд (2) также расход, методом от противного. Допустим, что (2) - сход, тогда по док-му в пункте а) ряд (1) должен сход, что противоречит усл. => (2) - расход.

Пр: (1) å_к=1^∞1/к^1/2 сравним его с рядом (2) å_к=1^∞1/к – гармонический ряд расходится.

Так как к^1/2£к, то 1/к^1/2³1/к

По приз. сравн. ряд (1) также расх.

Т2: (предельный признак сравнения).

Пусть даны полож. ряды (1) å_к=1^∞а_к (а_к³0) и å_к=1^∞ b_k (b_k >0), если сущ. предел lim_n®∞a_k/b_k=A (A≠0; A≠∞), то ряды (1) и (2) сход. или расход. одновременно.

Док-во: Т.к. lim_n®∞a_k/b_k=A, то по опред. предела ("e>0), ($N)("n) (n³NÞ| a_n/b_n-A| < e),

-e<a_n/b_n-A<e

A-e<a_n/b_n<A+e (3)

a) пусть (1) – сход, тогда при e< А из левой части нер. (3) получ.:

b_k<1/(A-e)*a_k. Из св-ва умнож. ряда на число получ., что ряд å_к=1^∞1/(A-e)*a_k - сход. Тогда по призн. сравн. в неравенствах ряд (2) также сход.

Мы доказ, что ряды (1) и (2) сход одновременно, значит и расход одновременно.

Признак Даламбера:

Т: пусть дан ряд (1) å_к=1^∞а_к (а_к>0), если сущ предел отношения последующего члена ряда предыдущему lim_n®∞a_k+1/а_k=ℓ, то

а) если ℓ<1, то ряд (1) сход, б) если ℓ>0, то ряд (1) – расход.

Док-во: а) пусть ℓ<1

Возьмем число ℓ<q<1, тогда для (e = q - ℓ) ($N) ("n) (n³N Þ a_n+1/a_n<q)

Или а_n+1<a_n*q

Возьмем n=N, N+1,...,N+p...

Получ: а_N+1<a_N*q

a_N+2<a_N+1<a_N*q²,.... a_N+p+1<a_N+p<a_N*q^p+1

рассмотр ряды: a_N+1+a_N+2+...+a_N+p+1+... (остаток ряда (1)) и a_N*q+a_N*q²+...+ a_N*q^p+1+...(геом прогр, знаменат q<1) – т.е. этот ряд сход. Тогда по призн сравн в неравенствах остаток ряда (1) сход, а значит и ряд (1) – сход.

б) пусть ℓ>1

тогда рассуждая аналог, получ, что при

e=ℓ-1 члены послед-и (а_n+1/a_n) будут нах-ся, начиная с некот, в e окрестности т.е. а_n+1/a_n>1, a_n+1>a_n., т.е. члены ряда положит и возрастают, т.е. lim_n®∞a_n¹0. В последствии из необход признака ряд расх.

Замеч: Если ℓ=1, то призн Д. не дает ответа на вопрос о сход или расход ряда, т.е. есть как сходимые, так и расходимые ряды, у которых ℓ=1.

Пр: å_n=1^∞n/2ⁿ

a_n=n/2ⁿ

a_n+1= (n+1)/2ⁿ⁺¹

lim_n®∞(a_n+1/a_n)= lim_n®∞((n+1)*2ⁿ)/(2ⁿ⁺¹*n)= lim_n®∞((n+1)/2n)=1/2 <1 => ряд сходится.

Признак Коши:

Т: пусть дан положительный ряд (1) å_к=1^∞а_к (а_к³0) и $-ет lim_n®∞(а_n)^1/n=ℓ, тогда

а) если ℓ<1, то ряд (1) – сходится.

б) если ℓ>1, то ряд (1) – расходится.

Док-тво: а) пусть ℓ<1.

Возьм число ℓ<q<1

Т.к. lim_n®∞(а_n)^1/n=ℓ, то все члены послед-и (а_n)^1/n, начиная с некот будут в e окрестн точки ℓ, т.е. для (e=q - ℓ) ($N) ("n) (n³N Þ (а_n)^1/n <q)

а_n<qⁿ

т.к. ряд q^N + q^N+1 +...+ q^N+p +... – сход (геом прогр с 0<q<1), то призн сравн в неравенствах ряд a_N+ a_N+1 +...+ a_N+p +...- сход, а он является (N-1)-ым остатком ряда (1), тогда и ряд (1) – сход.

б) пусть ℓ>1.

Аналог рассуждая получаем, что (а_n)^1/n >1, a_n>1, а значит предел общего чл ряда (1) не м.б. =0, => (1)- расх.

Зам: при ℓ=1 призн К ответа не дает, но можно доказ, что призн К сильнее признака Даламбера, т.е. если ответ дает призн Д, то и призн К также дает ответ, но есть случаи, когда в признаке Д ℓ=1, а в признаке К ℓ¹1.

Пр: å_к=1^∞(n/(2n+1))ⁿ, lim_n®∞((n/(2n+1))ⁿ)^1/n = lim_n®∞(n/(2n+1))=1/2 <1 => ряд сх.

Интегр призн сход-и рядов:

Т: пусть дан ряд (1) å_к=1^∞а_к (а_к³0). Если на полуинтервале [1; +∞] сущ положит непрер монот убыв ф f(x), такая что f(n)=a_n для всех n, то ряд (1) и несобств-й интеграл [1; +∞] f(x)d(x) – сход или расход одноврем.

Знакочередующиеся ряды:

О: ряд (1) å_к=1^∞(-1)^к-1а_к, где все а_к>0, kÎN (a_k<0), называется знакочер.

Т. Лейбница:

Если lim_n®∞(а_n)=0 и члены ряда (1) монот убыв по абсолютной величине, т.е. а₁> а₂>...> а_n> а_n+1>..., то ряд (1) сход. Сумма ряда одного знака с 1 членом, а по абсолютной |S_n|£а₁.

Док-во: рассм част сумму ряда с четным числом чл S_2n=(a₁-a₂)+ (a₃-a₄)+...+ (a_2n-1-a_2n), т.к. все слаг полож, то послед (S_2n) монот возраст. Сгруппируем чл другим обр: S_2n=a₁-(a₂-a₃)- (a₄-a₅)-...-a_2n, т.к. из а₁ вычитаются полож числа, то S_2n£a₁.

Послед (S_2n) монот возраст и огранич сверху, и по теор она сход, т.е. сущ lim_n®∞(S_2n)=S.

Покаж, что послед частич сумм с нечет числом чл также сход к числу S.

S_2n+1=S_2n + a_2n+1

lim_n®∞(S_2n+1)= lim_n®∞(S_2n)+ lim_n®∞(a_2n+1)=S+0=S.

Итак, послед-и частич сумм как с четн так и нечет числом чл имеют один предел и значит: lim_n®∞(S_n)=S, т.е. ряд (1) – сход.

Сл: если сумма ряда типа Л заменить» его частич суммой, то абсолютная величина погрешности не превосходит абсолютной величины 1-го отброшенного члена.