Примеры решения задач. Какое увеличение дает лупа, оптическая сила которой 16Дптр?

Задача 1.

Какое увеличение дает лупа, оптическая сила которой 16Дптр? Построить изображение предмета в лупе.

Решение.

Увеличение, даваемое лупой, рассчитывают по формуле:

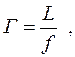
где 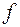– фокусное расстояние лупы; – расстояние наилучшего зрения (равно 25 см для нормального глаза).

Следовательно,

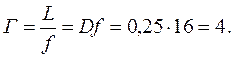
Для того чтобы рассмотреть предмет через лупу, его располагают между лупой и ее фокусом (Рис. 1).

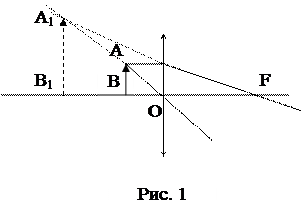Для построения изображения точки А этого предмета используем два луча, исходящих из нее: один, параллельный главной оптической оси, после преломления проходит через фокус; другой, проходящий через главный оптический центр линзы, не изменит своего направления. Изображение А ₁ точки А получается в точке пересечения продолжений преломленных лучей. Аналогично получаем изображение В ₁ точки В. Следовательно, изображение А ₁ В ₁ предмета АВ будет мнимое, увеличенное и прямое.

Ответ: изображение предмета АВ будет мнимое, увеличенное в 4 раза и прямое.

Задача 2.

Вывести с помощью принципа Ферма формулу преломления параксиальных лучей на сферической поверхности радиуса R, разделяющей среды с показателями преломления 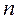и .

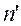Решение.

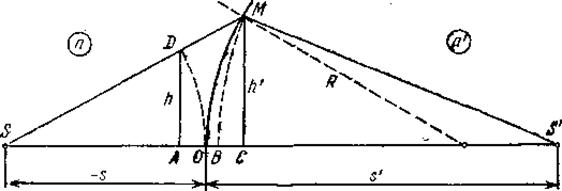
Параксиальные (приосевые) лучи – это лучи, образующие с оптической осью малые углы. Пусть S – точечный источник света и 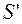– его изображение (Рис. 2). По принципу Ферма оптические длины всех лучей, вышедших из S и собравшихся в 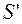, одинаковы. Проведем окружности из центров S и 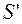радиусами SO и 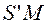. Тогда оптические пути (DM) и (OB) должны быть равны:

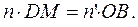(1)

Но для параксиальных лучей:

,

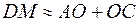где

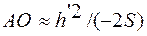и .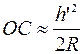

Кроме того,

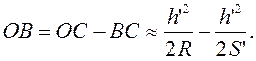
Подставив эти выражения в (1) и имея в виду, что 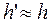, получим:

.

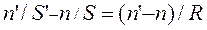Ответ: .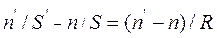

Задача 3.

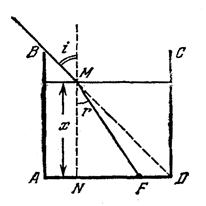
Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя не видит его дна, но полностью видит стенку CD (Рис. 3).

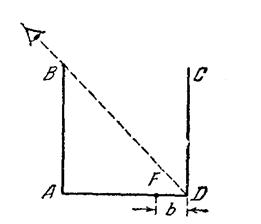
Какое количество воды нужно налить в сосуд, чтобы наблюдатель смог увидеть предмет F, находящийся на расстоянии b =10 см от угла D? Ребро сосуда а =40 см.

Решение.

Минимальное количество воды, определяемое уровнем x (Рис. 3а), можно найти из треугольника MNF, NF=x-b=x·tg r.

Дано:	СИ:	Рис. 3а
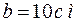=	0,1 м
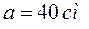=	0,4 м
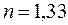
Найти: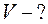

Из закона преломления: sin r= sin i/n.

.

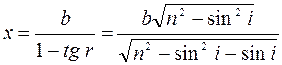Подставив значения и произведя вычисления, получим:

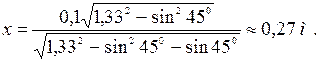
Необходимый объем воды:

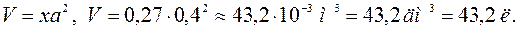
Ответ: 43,2 л.

Задача 4.

Найти положение главных плоскостей, фокусов и узловых точек двояковыпуклой тонкой симметричной стеклянной линзы с радиусом кривизны поверхностей R =7,50 см, если с одной стороны ее находится воздух, а с другой – вода.

Решение.

Главные плоскости совпадают с центром линзы. Фокусные расстояния в воздухе и воде:

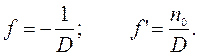
Оптическая сила линзы равна:

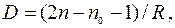
где 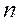и 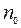- показатели преломления стекла и воды.

Из справочных таблиц для стекла 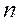=1,5 и для воды 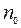=1,33. Согласно условию R =7,50 см или R =0,075 м.

Произведя вычисления, получим:

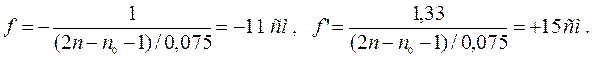
Узловые точки совпадают и расположены в воде на расстоянии:

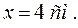
Задача 5.

Телеобъектив состоит из двух тонких линз – передней собирающей и задней рассеивающей с оптическими силами D ₁=+ 10 Дптр и D₂=-10 Дптр. Найти фокусное расстояние и положение главных плоскостей этой системы, если расстояние между линзами d =4,0 см.

Решение.

Оптическая сила системы:

D=D ₁ +D ₂ - d D ₁ D ₂.

Подставляя числовые значения, получаем:

D= +10 – 10 – 0,04·10·(-10) = +4 (-10) = +4 Дптр.

Фокусное расстояние равно:

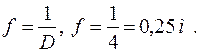
Определим расстояния, на которых расположены обе главные плоскости от линз.

Передняя главная плоскость находится перед собирающей линзой на расстоянии: 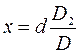, вычисляя, получаем: .

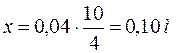Задняя главная плоскость расположена на расстоянии 0,10 м от рассеивающей линзы:

.

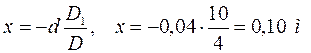Ответ: f =0,25 м; передняя главная плоскость находится перед собирающей линзой на расстоянии 0,10 м; задняя главная плоскость – на расстоянии 0,10 м от рассеивающей линзы.

Задача 6.

В вершинах равнобедренного треугольника расположены источники света S ₁ и S ₂ равной силы (Рис. 4). Как следует расположить маленькую пластинку А, чтобы освещенность ее была максимальной? Стороны треугольника AS ₁ =AS ₂= а.

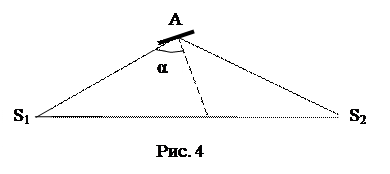
Решение.

Если нормаль к пластинке составляет угол α с направлением AS ₁, то освещенность пластинки:

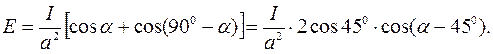
Следовательно, освещенность пластинки будет максимальна, если она параллельна стороне треугольника S ₁ S ₂.

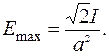
Ответ: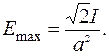

Задача 7.

Почему сквозь папиросную бумагу можно прочесть текст только в том случае, если бумагу непосредственно наложить на страницу книги?

Решение.

Папиросная бумага рассеивает во все стороны падающие на нее световые лучи. Если бумага находится на некотором расстоянии от текста книги, то расходящиеся пучки света, отраженные от белых участков страницы (между буквами), перекрываются на стороне папиросной бумаги, обращенной к тексту (Рис. 5).

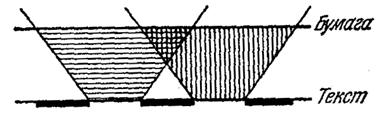
В результате бумага окажется освещенной приблизительно равномерно, и вследствие рассеяния ею света прочитать текст будет нельзя. Если бумага непосредственно наложена на текст, то освещенность прилегающей к тексту стороны бумаги не будет равномерной. Соответственно интенсивность рассеянного света будет различной в различных участках листа бумаги. Это и позволяет прочитать текст.

Задача 8.

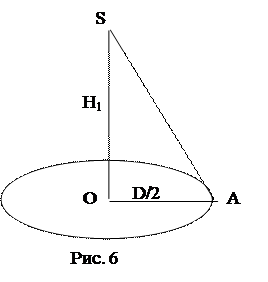На высоте Н ₁=2 м над серединой круглого стола (Рис. 6) диаметром D =3 м висит лампа в I ₁=100 Кд. Ее заменили лампой в I ₂=25 Кд, изменив расстояние до стола так, что освещенность середины стола осталась прежней. Как изменится освещенность края стола?

Дано:	Решение. Сделаем чертеж.
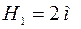
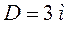
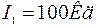
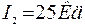
Найти: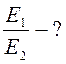

Освещенность середины стола:

,

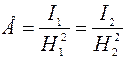где 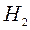- высота второй лампы над столом.

Освещенность края стола в первом случае равна:

,

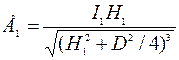во втором случае:

.

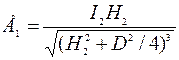Отсюда

.

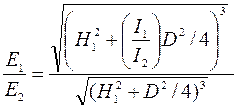Подставив значения, получим:

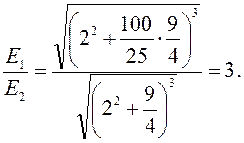
Освещенность края стола уменьшится в 3 раза.

Ответ: освещенность края стола уменьшится в 3 раза.

Домашнее задание:

[Л-3] – 15.14, 15.35, 15.38, 15.41, 15.59, 15.62, 15.63, 15.66, 15.67, 15.68;

[Л-4] – 4.3, 4.6, 4.8, 4.9, 4.10, 4.14, 4.14, 4.24, 4.26, 4.27;

[Л-5] – 5.11, 5.15, 5.16, 5.18, 5.29, 5.30, 5.35.

Вопросы для самопроверки

1. Что называют фотометрией?

2. Как построить изображение предмета, если он значительно больше линзы?

3. Почему в тонкостенном стакане с водой ложечка кажется увеличенной?

4. При каком условии непрозрачный предмет дает тень без полутени?

5. Как должна быть расположена лампочка в карманном фонаре относительно главных фокусов собирающей линзы и вогнутого зеркала?

6. Как надо расположить собирающую и рассеивающую линзы, чтобы параллельные лучи, пройдя через линзы, остались параллельными? При всяких ли линзах возможно решение этой задачи?

7. Почему в фотометрии вводятся двойные величины (энергетические и визуальные)?

8. Что называется энергетическим световым потоком?

9. Связь между светимостью и яркостью.

10. Определение единицы светового потока – люмена.

11. Определение единицы освещенности – люкса.

12. Зависит ли яркость раскаленного шара от расстояния до него?

13. Часто под действием солнечных лучей снег на крыше тает, а на почве нет. Почему?

14. В какое время дня освещенность земной поверхности большая?

Date: 2015-05-08; view: 11567; Нарушение авторских прав