Примеры решения задач. На пленку ( ) под углом падает белый свет

Задача 1.

На пленку (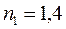 ) под углом 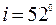падает белый свет. При какой толщине пленка в проходящем свете будет казаться красной? Длина волны красного света 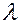= 6,7·10^-7 м.

Анализ.

При попадании на пленку свет частично проходит, частично отражается от поверхности пленки. Поскольку наблюдение ведется в проходящем свете, то интерферируют две волны, одна из которых проходит через пленку без отражения, вторая - испытав отражение на обеих поверхностях пленки. Результат интерференции в точке наблюдения будет зависеть от оптической разности хода лучей.

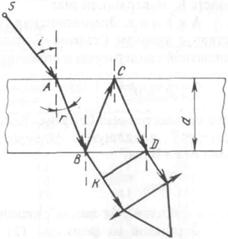
Решение.

Луч от источника падает на пластинку, частично преломляясь и отражаясь в точках А, В, С и D. (Рис. 3). Отражение луча в точке С не сопровождается потерей полуволны, поэтому оптическая разность хода лучей SAВК и SАВСD:

,

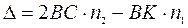где 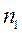- показатель преломления стекла; 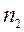- показатель преломления воздуха.

В результате преобразований получим:

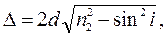
где d- толщина пленки; 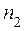- показатель преломления пленки; 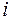- угол падения луча.

Условием максимума, т.е. условием того, что пленка будет казаться окрашенной, является равенство:

Дляминимальной толщины пленки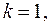

так что:

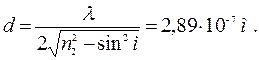
Ответ: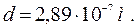

Задача 2.

При наблюдении колец Ньютона в отраженном свете 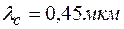с линзы, положенной на плоскую пластинку, радиус третьего светлого кольца равен 1,06 мм. После замены синего светофильтра на красный был измерен радиус пятого светлого кольца, оказавшийся равным 1,77 мм. Найти радиус кривизны 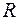линзы и длину волны 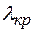красного света.

Решение.

Дано:	СИ	Рис.4.

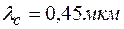
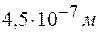
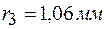
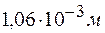
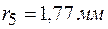
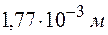
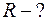
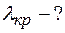
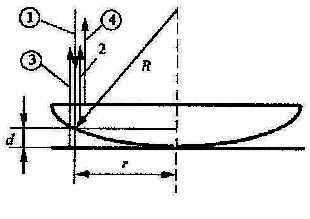
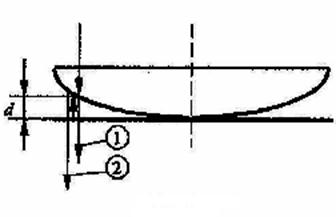
1. Ход лучей в установке для наблюдения колец Ньютона изображен на Рис.4. Падающий луч 1 проходит через плоскую поверхность линзы и разделяется на сферической поверхности на два луча.

Один из них (луч 2 на Рис.4), возникающий в результате отражения падающего луча, выходит из линзы в обратном направлении. Так как радиус 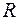сферической поверхности линзы, как правило, велик, то луч 2 распространяется практически параллельно падающему лучу 1. Второй луч (обозначен цифрой 3 на Рис. 4) проходит через зазор между линзой и плоской пластиной и после отражения от пластины также идет в обратном направлении по отношению к падающему лучу. Эти два луча и создают интерференционную картину в отраженном свете. Лучи, возникающие в результате многократного отражения от оптических поверхностей, гораздо слабее по интенсивности, по сравнению с рассмотренными, и заметного влияния на интерференционную картину не оказывают.

На первый взгляд может показаться, что луч 4, возникающий при отражении от плоской поверхности линзы, также должен интерферировать с лучами 2 и 3, однако на практике такая интерференция не наблюдается. Это объясняется тем, что плоская поверхность линзы при установке линзы на плоскую пластину образует с ней достаточно большой угол, так что ширина полос, возникающих при интерференции лучей 2-4 и 3-4 очень мала и полосы не видны. В предыдущем примере мы видели, что для видимого света интерференцию в клине можно наблюдать лишь при малых углах клина (несколько десятков угловых секунд), что практически никогда не выполняется в установке для наблюдения колец Ньютона без принятия специальных мер. Поэтому луч 4 никакого влияния на интерференционную картину не оказывает. Легко убедиться, что интерференционная картина, возникающая при наложении лучей 2 и 3, не зависит от смещения центра сферической поверхности от нормали к поверхности плоскопараллельной пластины.

2. Оптическая разность хода лучей 2 и 3 возникает в промежутке между сферической поверхностью линзы и плоской поверхностью пластинки. Обозначим толщину этого промежутка 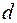. Тогда оптическая разность хода 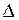будет равна:

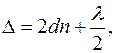(2.1)

где 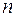- показатель преломления среды, заполняющей промежуток.

Дополнительная разность хода 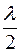возникает при отражении одного из интерферирующих лучей от оптически более плотной среды (обычно это имеет место для луча З).

Толщину промежутка 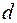найдем из геометрических соображений:

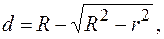
где 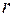- расстояние от центра интерференционной картины до точки наблюдения.

Диаметр линзы обычно значительно меньше радиуса кривизны ее поверхности, т.е. 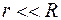и тогда можно приближенно записать

(2.2)

Окончательно получим:

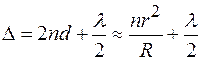(2.3)

Из полученного выражения следует, что для всех точек, равноудаленных от вершины сферической поверхности, интерференционная картина имеет вид чередующихся темных и светлых колец, центр которых совпадает с вершиной сферической поверхности линзы.

3. Радиусы темных и светлых колец определим из условия максимумов и минимумов интенсивности в интерференционной картине:

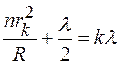- светлое кольцо (2.4)

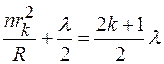- темное кольцо (2.5)

Отсюда находим выражения для радиусов 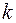-го светлого и темного колец

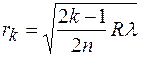- радиус 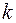-го светлого кольца, (2.6)

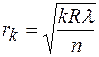- радиус 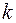-го темного кольца. (2.7)

В центре интерференционной картины в отраженном свете всегда наблюдается темное пятно, т.к. при 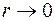, оптическая разность хода 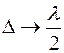, как это следует из Рис. 5.

4. По условию задачи известен радиус третьего светлого кольца, поэтому в соответствии с (2.6) с учетом того, что промежуток между линзой и плоской пластинкой заполнен воздухом (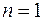 ), можно записать:

.

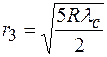Отсюда находим радиус сферической поверхности линзы:

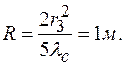
Определив радиус кривизны поверхности линзы, по известному радиусу пятого светлого кольца при наблюдении в красном свете находим длину волны :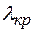

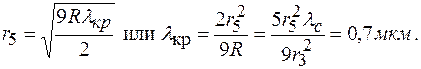
Примечание.

1. Кольца Ньютона можно наблюдать и в проходящем свете. В этом случае будут интерферировать падающий луч 1 (после прохождения линзы и плоскопараллельной пластинки) и луч 2, испытавший отражение на плоской поверхности пластины и сферической поверхности линзы (Рис. 5). Оптическая разность хода будет возникать за счет двукратного прохождения лучом 2 промежутка d между указанными поверхностями.

2. Однако дополнительной разности хода 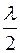не будет, так как луч 2 испытывает четное число отражений. Поэтому при наблюдении колец Ньютона в проходящем свете оптическая разность хода 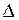определяется выражением:

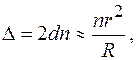(2.8)

а радиусы темных и светлых колец будут равны:

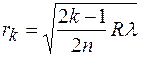радиус 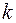-го темного кольца, (2.9)

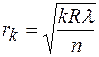- радиус -го светлого кольца. (2.10)

Из сравнения приведенных формул с формулами (2.6) и (2.7) видно, что в проходящем и отраженном свете темные и светлые кольца меняются местами, т.е. в том месте, где в отраженном свете наблюдается темное кольцо, в проходящем свете будет светлое кольцо и наоборот. Такое обращение контраста находится в полном соответствии с законом сохранения энергии.

Задача 3.

Два когерентных источника S₁ и S₂ с длиной волны 0,5 мкм находятся на расстоянии 2 мм друг от друга. Параллельно линии, соединяющей источники, расположен экран на расстоянии 2 м от них. Что будет наблюдаться в точке А экрана: свет или темнота?

Решение.

В точке А экрана будет свет, если разность хода двух лучей, исходящих из источников S₁ и S₂, равна целому числу длин волн, и темнота, если эта разность хода равна нечётному числу полуволн. Вычислим разность хода:

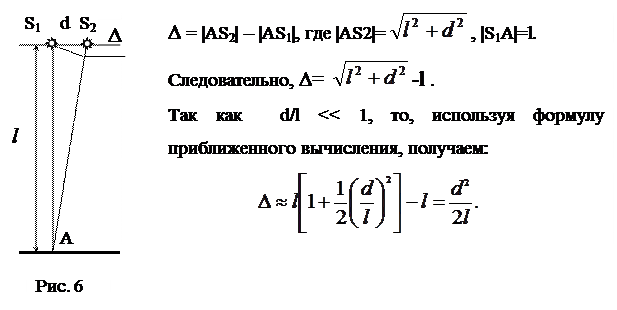Вычисляя, получаем:

D » .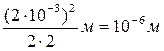

Сравнивая значения D и l, видим, что разность хода равна целому числу длин волн (двум), следовательно, в точке А экрана будет свет.

Ответ: в точке А экрана будет свет.

Задача 4.

Найти радиус кривизны линзы, применяемой для наблюдения колец Ньютона, если расстояние между вторым и третьим светлыми кольцами 0,5 мм. Установка освещается светом с длиной волны 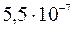м. Наблюдение ведется в отраженном свете.

Решение.

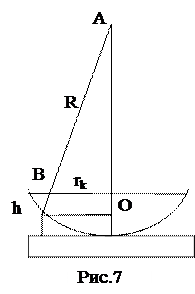
Из треугольника ОАВ (Рис. 7) имеем:

|BA|² = |BO|² + |AO|², или R² = r²_k + (R - h)² , откуда r²_k – 2Rh + h² = 0.

Пренебрегая малой величиной h² по сравнению с остальными слагаемыми, получим r_k= 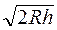. Иначе, для светлого k-ого кольца в отраженном свете разность хода равна: ,

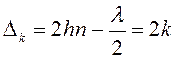откуда

2h = (2k + 1) .

Тогда

r_k = ,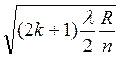

для k = 2: r₂ = = ,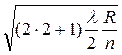

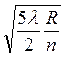для k = 3: r₃ = =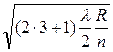

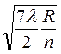
Тогда Dr_3,2 = r₃ – r₂ = 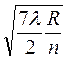- 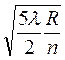= 0,4 ,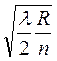

Откуда:

R = 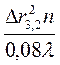= 5,7 м.

Ответ: R=5,7 м.

Задача 5.

Некоторое колебание возникает в результате сложения N когерентных колебаний одного направления, имеющих следующий вид:

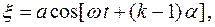
где k – номер колебания (k=1, 2, 3, N), 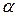- разность фаз между k-м и (k-1)-м колебаниями. Найти амплитуду результирующего колебания.

Решение.

Сопоставим каждому колебанию вектор, модуль которого равен а. Угол между векторами, характеризующими k-е и (k+1)-е колебания, по условию, равен 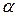. Изобразим из этих N векторов цепочку (Рис. 8) и обозначим результирующий вектор как А. Мысленно проведем описанную окружность радиуса R с центром в точке О.

Тогда, как видно из Рис.8:

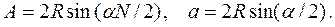
Исключив R из этих двух уравнений, получим:

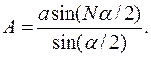
Ответ: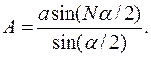

Домашнее задание:

[Л-3] - 16.4, 16.5, 16.9, 16.10, 16.13 16.14,16.15;

[Л-4] – 4.31, 4.32, 4,36, 4.35;

[Л-5] - 5.41,5.45,5.51,5.58,5,62.

Вопросы для самопроверки

1. Находится ли явление интерференции в согласии с законом сохранения энергии? Ответ обоснуйте.

2. Можно ли наблюдать интерференцию световых пучков, излучаемых двумя разными лазерами? Двумя одинаковыми лампами?

3. Как можно наблюдать интерференцию света от некогерентных источников света?

4. Каковы условия интерференционных максимумов и минимумов?

5. В чем заключается суть методов получения когерентных пучков делением волнового фронта?

6. В чем отличия интерференционных картин при освещении двух щелей монохроматическим и белым светом?

7. При каком условии наблюдается четкая интерференционная картина, создаваемая на экране двумя когерентными источниками?

8. Что происходит с четкостью интерференционной картины с увеличением номера m полосы?

9. Что такое полосы равной толщины, равного наклона?

10. В чем отличие интерференционных картин, полученных в отраженном и проходящем свете?

11. Почему центр колец Ньютона, наблюдаемый в проходящем свете, обычно светлый?

12. Как изменится картина колец Ньютона, если пространство между линзой и пластинкой заполнить водой?

13. Почему при наблюдении колец Ньютона линзу выбирают с большим радиусом кривизны?

14. При помощи зеркал Френеля получили интерференционные полосы, пользуясь красным светом. Как изменится картина интерференционных полос, если воспользоваться фиолетовым светом?

15. Как объяснить радужные полосы, наблюдаемые в тонком слое керосина на поверхности воды?

16. Если мыльную пленку расположить вертикально, то цветные горизонтальные полосы будут с течением времени перемещаться вниз, несколько изменяя свою ширину. Через некоторое время в верхней части пленки возникнет быстро увеличивающееся черное пятно, а затем пленка разорвется. Почему?

17. Чем объясняется расцветка крыльев стрекоз, жуков и прочих насекомых? Почему меняется окраска крыльев насекомого, если его рассматривать под разными углами?

Date: 2015-05-08; view: 6979; Нарушение авторских прав