Основные отношения школьной геометрии

Использование алгебраического метода основывается на связях между элементами фигур. Из школьного курса известно, что:

· сумма смежных углов равна 180 ;

· вертикальные углы равны;

· в равнобедренном треугольнике углы при основании равны;

· если в треугольнике два угла равны, то стороны против них также равны;

· в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;

· сумма углов треугольника равна 180 ;

· внешний угол треугольника равен сумме внутренних углов, не смежных с ним;

· серединные перпендикуляры к сторонам треугольника пересекаются в одной точке – центре описанной около этого треугольника окружности;

· биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанной в этот треугольник окружности;

· при пересечении двух прямых а и b третьей прямой с внутренние накрест лежащие углы равны тогда и только тогда, когда а || b;

· противоположные стороны выпуклого четырёхугольника равны тогда и только тогда, когда этот четырёхугольник – параллелограмм;

· диогонали четырёхугольника точкой пересечения делятся пополам тогда и только тогда, когда этот четырёхугольник – параллелограмм;

· параллелограмм имеет равные диагонали тогда и только тогда, когда он – прямоугольник;

· параллелограмм имеет взаимно перпендикулярные диагонали тогда и только тогда, когда он – ромб;

· если на одной стороне угла параллельные прямые отсекают равные отрезки, то при пересечении их с другой стороной угла также возникают равные отрезки (теорема Фалеса);

· средняя линия треугольника параллельна третьей стороне и равна её половине;

· средняя линия трапеции параллельна основаниям и равна их полусумме;

· параллельные прямые отсекают на сторонах угла пропорциональные отрезки;

· в треугольнике квадрат большей стороны равен сумме квадратов двух других сторон тогда и только тогда, когда этот треугольник прямоугольный;

· для любых трёх точек А, В, С, лежащих на одной прямой, АВ = АС + СВ или АВ = АС – СВ;

· центральный угол окружности измеряется дугой, на которую опирается;

· вписанный в окружность угол измеряется половиной дуги, на которую опирается;

· произведение частей хорды, на которые она делится своей точкой М, одно и то же для всех хорд, проведённых через М;

· произведение секущей, проведённой через точку М, находящуюся вне окружности, на её внешнюю часть одно и то же для всех секущих, проведённых через М;

· квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними (теорема косинусов);

· стороны треугольника пропорциональны синусам противолежащих углов (теорема синусов);

· в треугольнике против большего угла лежит большая сторона;

· в треугольнике против большей стороны лежит больший угол;

· отношение длины окружности к её диаметру есть величина постоянная (константа), она обозначается p;

· для вычисления площадьи S некоторых фигур применяют формулы:

S _{прямоугольника} = ab, где а и b – измерения прямоугольника;

S _{параллелограмма} = аh, где а – сторона параллелограмма, h – высота к ней;

S _{треугольника} = аh, где а – сторона треугольника, h – высота к ней;

S _{треугольника} = аb sіnÐ C, где а и b – стороны треугольника, С –угол между ними;

S _{треугольника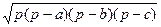} = , где а, b, c – стороны треугольника,

р = (а+b+c) –его полупериметр;

S _{трапеции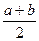} = h, где а и b – основания трапеции, h – проведённая к ним высота;

S _круга = p r ² , где r – радиус круга;

S _{сектора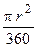} = a, где r – радиус сектора, a – его градусная мера;

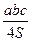· R = , r = 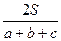, a, b, c – стороны треугольника, S – его площадь, R и r – радиусы описанной около него и вписанной в него окружностей соответственно;

· площади подобных фигур относятся как квадраты их линейных размеров;

· S _пр = S ₀ cos j, где S ₀ – площадь фигуры Ф, размещённой в плоскости a, S _пр – площадь ортогональной проекции фигуры Ф на плоскость b, j – двугранный угол между плоскостями a и b;

· противолежащие грани параллелепипеда параллельны и равны;

· диагонали параллелепипеда пересекаются в одной точке и делятся ей пополам;

· квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений;

· для вычисления боковых поверхностей тел применяются формулы:

§ S _{бок.цилиндра} = 2 p rh, где r – радиус основания цилиндра, h – его высота;

§ S _{бок. конуса} = p rl, где r – радиус основания конуса, l – его образующая;

§ S _шара = 4 p r ² , где r – радиус шара;

· для вычисления объёмов тел применяют следующие формулы:

§ V _{прямоуг.параллелепипеда} = abc, где a, b, c – измерения прямоугольного параллелепипеда;

§ V _призмы = S _осн. Н, где S _осн. – площадь основания призмы, Н – её высота;

§ V _{пирамиды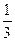} = S _осн. Н, где S _осн. – площадь основания пирамиды, Н – её высота;

§ V _{усеч. пирамиды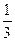} = _. Н (S ₁ + S ₂ + 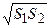), где H – высота усечённой пирамиды, S ₁, S ₂ – площади её оснований;

§ V _{цилиндра} = p r ² H, где r – радиус основания цилиндра, H – его высота;

§ V _конуса = 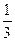_. p r ² Н, где r – радиус основания конуса, H – его высота;

§ V _{усеч. конуса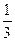} = _. pН (r ₁² + r ₁ r ₂ +r ₂² ), где H – высота усечённого конуса, r ₁ и r ₂ – радиусы его оснований;

§ V _шара = 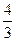p R³, где R – радиус шара;

§ V _{шар. сегмента} = p Н ² (R – 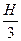), где R – радиус сегмента, H – его высота;

§ V _{шар. сектора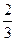} = pR ² Н, где R – радиус сектора, H – высота соответствующего шарового сегмента;

· объёмы подобных тел относятся как кубы их линейных размеров.

Date: 2015-05-05; view: 2016; Нарушение авторских прав