Теорема Пифагора

4.1. Теорема Пифагора – наверное самый известный факт геометрии. Она имеет богатую историю и сегодня известно более 360 ее доказательств, одно из которых приведем (рис. 9). Пусть дан прямоугольный треугольник с катетами a, b и гипотенузой с.

Чтобы доказать, что а ² + b ² = c ², построим два квадрата со стороной a + b.

Первый квадрат разобьем на два квадрата с площадями а ² и b ² и 4 прямоугольных треугольника, равных данному, другой – на четыре такие же треугольника и квадрат со стороной с.

Если от равных квадратов АВСD и А ₁ В ₁ С ₁ D ₁ отбросить по четыре равных треугольника, то оставшиеся фигуры будут иметь одинаковые площади. Поэтому

а ² + b ² = c ².

Теорема 1. В прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу:

= , = .

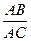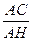Доказательство. Из подобия ∆АВС ~ ∆АСН и

∆АВС ~ ∆СВН получим необходимые пропорции.

Следствие 1. Хорда круга есть среднее пропорциональное между диаметром и её проекцией на диаметр, проходящий через один из концов хорды.

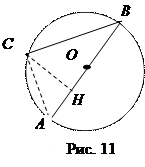Действительно, ÐACВ = 90° (рис. 11). Поэтому к треугольнику АВС можно применить теорему 1.

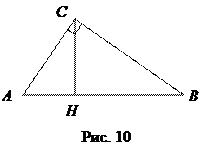
Теорема 2. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые она делит гипотенузу: = 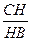(рис. 10).

Для доказательства достаточно заметить подобие треугольников АСН и СВН.

Следствие 2. В круге перпендикуляр, опущенный из какой-нибудь точки окружности на диаметр, есть среднее геометрическое между отрезками, на которые он делит диаметр: СН = 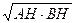(рис. 11).

Теорема 3. Разность квадратов двух сторон треугольника равна разности квадратов их проекций на третью сторону треугольника:

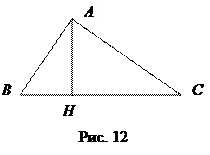АС ² – АВ ² = НС ² – НВ ² (рис. 12).

Доказательство. По теореме Пифагора, применённой к треугольникам АСН и АВН будем иметь:

АС ² = НС ² + АН ², АВ ² = НВ ² + АН ² ,

Откуда АС ² – АВ ² = НС ² – НВ ².

Следствие 3. Геометрическое место точек (ГМТ), разность квадратов расстояний которых до двух данных точек А и В постоянна, есть перпендикуляр к прямой АВ.

Действительно, пусть точки М и N такие, что МА ² – МВ ² = k и NA ² – NB ² = k. Спроектируем точку М на прямую АВ, получим точку О. Тогда АО ² – ВО ² = k. Если спроектировать точку N на прямую АВ, то для её проекции О ₁ будем иметь

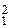АО – ВО 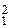= k. Значит, О ₁ = О.

Пусть теперь точка Р лежит на перпендикуляре ОМ, тогда для неё АО ² –ВО ² =k.

Теорема 4. Медиана треугольника равна половине стороны, к которой она проведена тогда и только тогда, когда она выходит из вершины прямого угла.

Доказательство. Необходимость. Пусть медиана СМ (рис. 13) в треугольнике АВС равна АВ, т.е. МА = МВ = МС.

Тогда Ð МСА = Ð А, Ð МСВ =Ð В,

Ð А + Ð В + Ð АСВ = 180º,

Ð А + Ð В = 90º, Ð МСА + Ð МСВ = 90º.

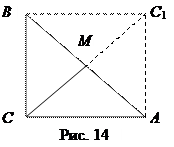
Достаточность. Пусть в прямоугольном треугольнике АВС, Ð С = 90º, проведена медиана СМ (рис. 14). Продолжим медиану СМ за точку М так, что МС ₁ = МС. Четырёхугольник АСВС ₁ – параллелограмм, причём Ð С = 90º, значит четырёхугольник АСВС ₁ – прямоугольник. Поэтому АВ = СС ₁ и МА = МВ = МС.

Следствие 4. Центр описанной около прямоугольного треугольника окружности находится на середине гипотенузы, а радиус окружности равен половине гипотенузы.

Задача 3. В прямоугольном треугольнике АВС из вершины С прямого угла проведена высота СН. Радиусы окружностей, вписанных в треугольники АСН и ВСН равны r ₁ и r ₂. Найти радиус r окружности, вписанной в треугольник АВС.

Решение. Из подобия треугольников ВАС, ВСН, САН можно записать 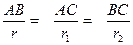. Тогда для определенного числа t: AB = rt, AC = r ₁ t, BC = r ₂ t.

А поскольку AB ² = AC ² +BC ², то r ² t ² = r 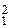t ² + r t ², и

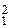r ² = r + r .

Заметим, что подобные отношения существуют между другими сходными линейными элементами d, d ₁ и d ₂ треугольников АВС, АСН и ВСН: d ² 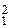= d + d , (например для расстояний от точки пересечения медиан до центров вписанных окружностей).

Этот факт называют обобщённой теоремой Пифагора.

Date: 2015-05-05; view: 1020; Нарушение авторских прав