Векторное произведение векторов и его свойства. Три некомпланарных вектора , и , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора кратчайший поворот от первого вектора

Три некомпланарных вектора , и , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора кратчайший поворот от первого вектора ко второму вектору виден совершающимся против часовой стрелки, и левую, если по часовой.

Определение. Векторным произведением вектора на вектор называется вектор , который:

1) перпендикулярен векторам и , то есть , ;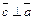

2) имеет длину 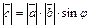, где ;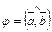

3) векторы , и образуют правую тройку.

Векторное произведение обозначается , то есть .

Из условия (2) следует, что длина вектора численно равна площади параллелограмма, построенного на векторах и , как на сторонах:

. (2.19)

Из определения векторного произведения вытекают следующие соотношения между ортам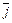и , и : , , .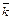

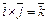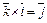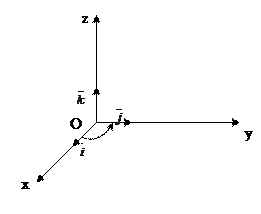
Свойства векторного произведения:

1) ;

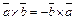2) ;

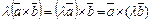3) ;

4) 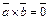тогда и только тогда, когда 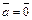, или , или ;

5) .

Из определения и свойств второго произведения следует: , , , .

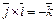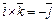Можно использовать таблицу векторного произведения векторов , 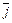и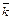

			-
	-
		-

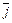
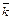
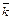
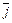
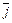
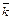
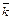
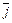
Пусть заданы два вектора и 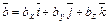. Тогда векторное произведение этих векторов может быть найдено с помощью определителя третьего порядка

. (2.20)

Пример 15. Упростить выражение .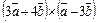

Решение. Используя свойства векторного произведения, получим

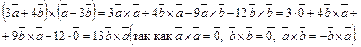
Пример 16. Вычислить площадь параллелограмма, построенного на векторах 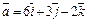и 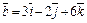, как на сторонах.

Решение. Найдем векторное произведение векторов и с помощью формулы (2.20):

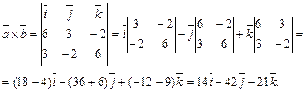
Так как модуль векторного произведения двух векторов равен площади построенного на них параллелограмма, то

Пример 17. Вычислить площадь параллелограмма построенного на векторах , если ,

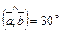
Решение. Найдем векторное произведение данных векторов:

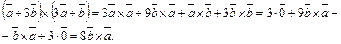
Площадь параллелограмма по формуле (2.19) равна , тогда получим .

Пример 18. Даны два вектора и . Вектор 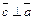, . Найти .

Решение. Так как вектор 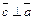и , тогда . Координаты вектора , вектора 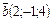. Найдем вектор , пользуясь формулой (2.20)

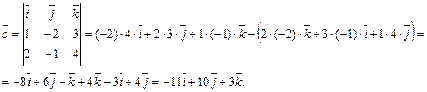
Таким образом вектор .

Найдем модуль вектора

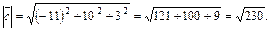
Пример 19. Найти , если известно, что , .

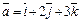Решение. Координаты вектора 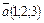, вектора 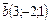. По формуле (2.18) найдем скалярное произведение векторов и

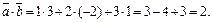
Найдем векторное произведение , используя формулу (2.20)

. Тогда искомое выражение .

Date: 2015-12-10; view: 1211; Нарушение авторских прав