
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Геометрический смысл модуля и знака Якобиана
Модуль якобиана есть предел отношения площадей бесконечно малых площадок Δ D и Δ D ΄.
Геометрический смысл знака якобиана состоит в том, что в случае положительного якобиана ориентации контуров, ограничивающих области D' и D при отображении совпадают, а при отрицательном — отличаются.
3.Двойной интеграл в полярной системе координат (как частный случай).
Связь между переменными в декартовой и полярной системах координат:
(см. рис. 2.2)
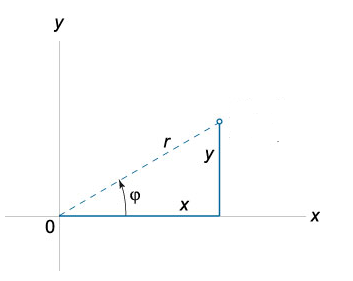
| Рисунок 2.2 |
 (2.5)
(2.5)
| Рисунок 2.3 |
 Якобиан при переходе в полярную систему координат:
Якобиан при переходе в полярную систему координат:  . (Убедитесь в этом, вычислив якобиан самостоятельно по формуле (2.2))
. (Убедитесь в этом, вычислив якобиан самостоятельно по формуле (2.2))
Теперь формула (2.3) примет вид:
 (2.6)
(2.6)
Заметим, что при переходе к полярным координатам область  не меняется.
не меняется.
Область интегрирования в полярной системе координат назовём радиально правильной, если она заключена в секторе между лучами 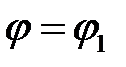 и
и  и ограничена в нём двумя, не пересекающимися во внутренних точках сектора, кривыми с уравнениями
и ограничена в нём двумя, не пересекающимися во внутренних точках сектора, кривыми с уравнениями  . (См. рис. 2.3)
. (См. рис. 2.3)
 преобразуется в повторный следующим образом:
преобразуется в повторный следующим образом:
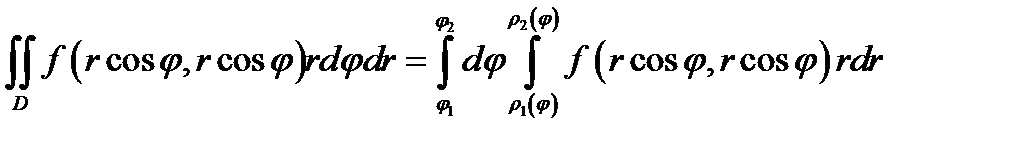 (2.7)
(2.7)
Площадь плоской фигуры в полярной системе координат вычисляется по формуле
 (2.8)
(2.8)
Замечание. К полярным координатам удобно переходить, когда подынтегральная функция зависит от  и в уравнениях границы области
и в уравнениях границы области  содержится эта же комбинация.
содержится эта же комбинация.
Пример 2.1 Область 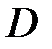 задана неравенствами
задана неравенствами  ,
, 
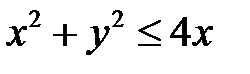 и
и  Преобразуем двойной интеграл
Преобразуем двойной интеграл  в повторный, изменим порядок интегрирования и перейдём к полярным координатам.
в повторный, изменим порядок интегрирования и перейдём к полярным координатам.
Решение. Построим заданную область, ограниченную двумя окружностями и прямой (см. рис. 2.4).
Выразим поочерёдно из уравнений всех частей границы, чему равны переменные  . Перейдём к полярной системе и выразим
. Перейдём к полярной системе и выразим 

(Обратите внимание на знаки перед корнями!)
Данная область не является 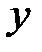 - правильной, т.к. её нижняя граница состоит из двух частей. Поэтому разобьём её на две части прямой
- правильной, т.к. её нижняя граница состоит из двух частей. Поэтому разобьём её на две части прямой 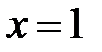 так, чтобы в каждой из этих частей было по одной нижней границе (см. рис. 2.4).
так, чтобы в каждой из этих частей было по одной нижней границе (см. рис. 2.4).

| Рисунок 2.4 |
Тогда 
 .
.
В 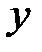 - правильной области
- правильной области  переменные изменяются так, что
переменные изменяются так, что 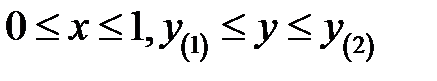 .
.
В 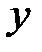 - правильной области
- правильной области  имеем
имеем  .
.
И тогда 
Пределы интегрирования в повторном интеграле расставлены.
Поменяем порядок интегрирования. Область  не является
не является 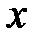 - правильной, т.к. её правая граница состоит из двух частей. Поэтому разобьём её на две части прямой
- правильной, т.к. её правая граница состоит из двух частей. Поэтому разобьём её на две части прямой  так, чтобы в каждой из этих частей было по одной правой границе (см. рис. 2.4). Тогда в
так, чтобы в каждой из этих частей было по одной правой границе (см. рис. 2.4). Тогда в  - правильной области
- правильной области  переменные изменяются так, что
переменные изменяются так, что  , а в
, а в 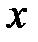 - правильной области
- правильной области 
 . И теперь
. И теперь 
Далее расставим пределы в повторном интеграле, перейдя к полярным координатам. Область  в полярной системе координат является радиально правильной, т.к. в ней переменные изменяются так, что
в полярной системе координат является радиально правильной, т.к. в ней переменные изменяются так, что  Отсюда следует, что
Отсюда следует, что 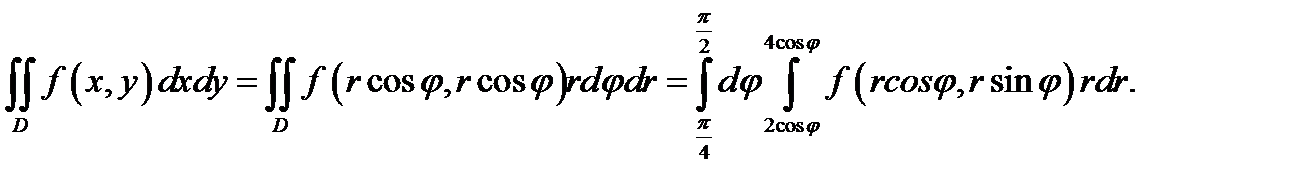
Выполнены все три варианта расстановки пределов в повторных интегралах.
4.Обобщённые полярные координаты.
При решении некоторых задач удобна следующая замена переменных, которая существенно упрощает вычисление интеграла.
 ,
, 
Здесь переменные 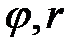 называются обобщёнными полярными координатами.
называются обобщёнными полярными координатами.
Пример 2.2 Вычислим площадь области, ограниченной астроидой  .
.
Решение. Построим астроиду (см. рис. 2.5).
Введём обобщённые полярные координаты:  , и показатель α подберём так, чтобы при подстановке в уравнение астроиды получилось уравнение единичной окружности. Для данной задачи такой показатель равен трём.
, и показатель α подберём так, чтобы при подстановке в уравнение астроиды получилось уравнение единичной окружности. Для данной задачи такой показатель равен трём.

Рисунок 2.5
Действительно,  , или
, или  .
.
Якобиан отображения при этом равен  .
.
Далее, по формуле (2.4) составим интеграл для вычисления искомой площади:
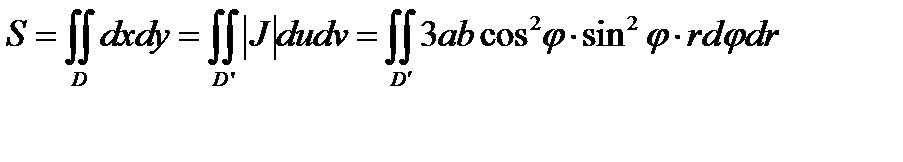 Область
Область 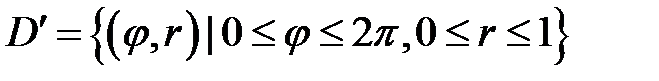 является радиально правильной. Расставим пределы в повторном интеграле и вычислим его.
является радиально правильной. Расставим пределы в повторном интеграле и вычислим его.
 .
.
Замечание. После расстановки пределов интегрирования оказалось возможным взять интегралы по  и
и 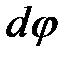 отдельно друг от друга, как их произведение, поскольку пределы внутреннего интегрирования постоянны.
отдельно друг от друга, как их произведение, поскольку пределы внутреннего интегрирования постоянны.
Домашнее задание к занятию 2: ОЛ-6 №№2161, 2163, 2167, 2170, 2181 или ОЛ-5 №№ 8.42, 45, 49, 51, 60, 63.
Дополнительный пример 2.3. Вычислить площадь замкнутой области  , образованной пересечением следующих кривых:
, образованной пересечением следующих кривых: 
Решить задачу с помощью перехода к новой системе координат. Проверить решение в среде MathCad.
Решение.
Если ввести координаты  , то в системе координат
, то в системе координат  область
область 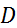 отобразится в область
отобразится в область  , представляющую собой прямоугольник, заключённый в пределах
, представляющую собой прямоугольник, заключённый в пределах  ,
,  . (См. рис.2.6)
. (См. рис.2.6)

Рисунок 2.6
Для вычисления площади области D применим формулу:

Сначала выразим переменные x и  через u и v, так как для вычисления Якобиана преобразования нам необходимо осуществить переход
через u и v, так как для вычисления Якобиана преобразования нам необходимо осуществить переход
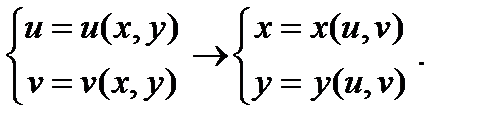 Получим систему:
Получим систему: 
 .
.
Якобиан преобразования: 
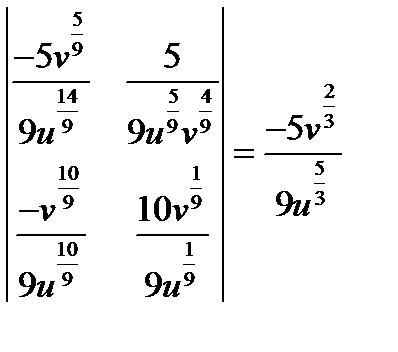
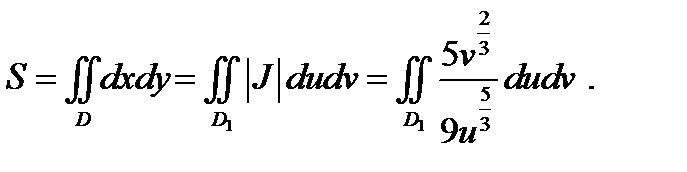
Область  , напомним, представляет собой прямоугольник (см.рис.2.6), подынтегральная функция может быть разбита на множители, поэтому при переходе от двойного интеграла к повторному он распадётся на произведение двух независимо вычисляемых интегралов:
, напомним, представляет собой прямоугольник (см.рис.2.6), подынтегральная функция может быть разбита на множители, поэтому при переходе от двойного интеграла к повторному он распадётся на произведение двух независимо вычисляемых интегралов:
 .
.
Date: 2015-10-19; view: 5942; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |