В знаменателе дроби

В школьном курсе при решении некоторых типов задач на освобождение от иррациональности в знаменателе дроби достаточно домножить числитель и знаменатель дроби на число сопряженное знаменателю.

Примеры. 1. t = .

Здесь в знаменателе срабатывает формула сокращенного умножения (разность квадратов), что позволяет освободиться от иррациональности в знаменателе.

2. Освободиться от иррациональности в знаменателе дроби

t = . Выражение – неполный квадрат разности чисел а = и b = 1. Воспользовавшись формулой сокращенного умножения а³ – b³= (а + b) · (a² – ab + b²), можно определить множитель m = (а + b) = + 1, на который следует домножать числитель и знаменатель дроби t, чтобы избавиться от иррациональности в знаменателе дроби t. Таким образом,

t = .

В ситуациях, где формулы сокращенного умножения не работают, можно использовать другие приемы. Ниже будет сформулирована теорема, доказательство которой, в частности, позволяет найти алгоритм освобождения от иррациональности в знаменателе дроби в более сложных ситуациях.

Определение 6.1. Число z называется алгебраическим над полем F, если существует многочлен f (x) F [ x ], корнем которого является z, в противном случае число z называется трансцендентным над полем F.

Определение 6.2. Степенью алгебраического над полем F числа z называется степень неприводимого над полем F многочлена p (x) F [ x ], корнем которого является число z.

Пример. Покажем, что числоz = 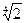является алгебраическим над полем Q и найдем его степень.

Найдем неприводимый над полем Q многочлен p (х), корнем которого является x = 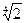. Возведем обе части равенства x = 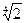в четвертую степень, получим х⁴ = 2 или х⁴ – 2 = 0. Итак, p (х) = х⁴ – 2, а степень числа z равна deg p (х) = 4.

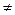Теорема 6.3 (об освобождении от алгебраической иррациональности в знаменателе дроби). Пусть z – алгебраическое число над полем F степени n. Выражение вида t = , где f (x), (x) F [ x ], (z) 0

единственным образом может быть представлено в виде:

t = с_n-1 z^n-1 + c_n-2 z^n-2 + … + c₁ z + c₀, c_i F.

Алгоритм освобождения от иррациональности в знаменателе дроби продемонстрируем на конкретном примере.

Пример. Освободиться от иррациональности в знаменателе дроби:

t =

1. Знаменателем дроби является значение многочлена (х) = х² – х +1 при х = 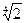. В предыдущем примере показано, что 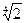– алгебраическое число над полем Q степени 4, так как оно является корнем неприводимого над Q многочлена p (х) = х⁴ – 2.

2. Найдем линейное разложение НОД ( (х), p (x)) с помощью алгоритма Евклида.

_ x⁴ – 2 | x² – x + 1

x⁴– x³+ x² x² + x = q₁ (x)

_ x³– x² – 2

x³– x²+ x

x² – x + 1 | – x –2 = r₁ (x)

x² + 2 x – x + 3 = q₂ (x)

_–3 x + 1

–3 x – 6

_ – x –2 |7 = r₂

– x –2 - x - = q₃ (x)

Итак, НОД ( (х), p (x)) = r₂ = 7. Найдем его линейное разложение.

Запишем последовательность Евклида, пользуясь обозначениями многочленов.

p (x) = (x) · q₁ (x) + r₁ (x) r₁ (x) = p (x) – (x) · q₁ (x)

(x) = r₁ (x) · q₂ (x) + r₂ (x) r₂ (x) = (x) – r₁ (x) · q₂ (x)

r₁ (x) = r₂ (x) · q₂ (x).

Подставим в равенство 7= r₂ (x) = (x) – r₁ (x) · q₂ (x) значение остатка r₁ (x) = p (x) – (x) · q₁ (x), после преобразований получим линейное разложение НОД( (х), p (x)): 7 = p (x) · (– q₂ (x)) + (x) · [1 + q₁ (x) · q₂ (x)]. Если подставить в последнее равенство вместо обозначений соответствующие многочлены и учесть, что p (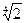) = 0, то имеем:

(1 – 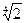+ ) · (– 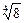+ 2 + 3 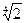+ 1)] = 7 (1)

3. Из равенства (1) следует, что если знаменатель дроби t умножить на число m = [1 + (– 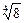+ 2 + 3 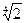+ 1)], то получим 7. Таким образом,

t = = .

МЕТОДИКА 16. Тема урока: Стандартный вид многочлена

Класс: 7

Тип урока: урок проверки и контроля знаний и умений

Цели урока:

- проверить умения приводить многочлен к стандартному виду

- развивать у учащихся логическое мышление, внимание

- воспитывать самостоятельность

Структура урока:

1) Организационный момент

2) Инструктаж

3) Самостоятельная работа.

Задания:

1. Дополните предложения:

а) Выражение, содержащее сумму одночленов называют …(многочленом).

б) Многочлен состоящий из стандартных одночленов и не содержащий подобных слагаемых называется … (стандартным многочленом).

в) Наибольшую из степеней одночленов входящих в многочлен стандартного вида называют … (степенью многочлена).

г) Прежде чем определить степень многочлена, нужно … (привести его к стандартному виду).

д) Для нахождения значения многочлена нужно сделать первое…(представить многочлен в стандартном виде), второе …(подставить значение переменной в данное выражение).

2. Найти значение многочлена:

а) 2a⁴-ab+2b² при a=-1, b=-0,5

б) x²+2xy+y² при x=1,2, y=-1,2

3. Привести многочлен к стандартному виду:

а) -5ах² + 7а²х + 2а²х + 9ах² – 4ах² – 8а²х;

б) (5х² – 7х – 13) – (3х² – 8х + 17);

в) 2а – (1,4ав + 2а² – 1) + (3а + 6,4ав);

г) (2с² – 1,6с + 4) – ((10,6с² + 4,4с – 0,3) – (3,6с² – 7с – 0,7));

4. Привести многочлен к стандартному виду и выяснить при каких значениях х его значение равно 1:

а) 2x²-3x-x²-5+2x-x²+10;

б) 0,3x³-x²+x-x³+3x²+0,7x³-2x²+0,07

Date: 2015-10-18; view: 2138; Нарушение авторских прав