Примеры решения задач. Пример 4. Колебательный контур, состоящий из воздушного конденсатора с двумя пластинами площадью S=100 см2 каждая и катушки с индуктивностью L=l мкГн

Пример 4. Колебательный контур, состоящий из воздушного конденсатора с двумя пластинами площадью S=100 см² каждая и катушки с индуктивностью L=l мкГн, резонирует на волну длиной λ=10 м. Определить расстояние d между пластинами конденсатора.

Решение. Расстояние между пластинами конденсатора можно найти из формулы электроемкости плоского конденсатора С=ε₀εS/d, где ε — диэлектрическая проницаемость среды, заполняющей конденсатор, откуда

d=ε₀εS/C (1)

Из формулы Томсона, определяющей период колебаний в электрическом контуре: 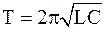, находим электроемкость

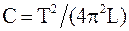. (2)

Неизвестный в условии задачи период колебаний можно определить, зная длину волны λ, на которую резонирует контур. Из соотношения λ =сТ имеем

Т= λ /с.

Подставив выражения периода Т в формулу (2), а затем электроемкости С в формулу (1), получим

.

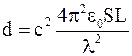Произведя вычисления, найдем d=3,14 мм.

6.5.1. Колебательный контур состоит из конденсатора емкостью С=5 мкФ и катушки с индуктивностью L=0,200 Гн. Определить максимальную силу тока I₀ в контуре, если максимальная разность потенциалов на обкладках конденсатора U₀=90 В. Активным сопротивлением контура R пренебречь.

Решение. Рассмотрим два способа решения задачи. Первый из них основан на исследовании уравнения свободных электромагнитных колебаний

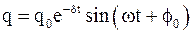, (1)

где 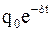– амплитуда свободных (затухающих колебаний);

=R/2L – коэффициент затухания;

w – циклическая частота;

q₀ – начальная амплитуда (определяется из начальных условий);

₀ – начальная фаза (определяется из начальных условий.

Второй способ основан на законе сохранения энергии.

1. Если в колебательном контуре сопротивление R пренебрежимо мало, то в уравнении (1), выражающем заряд конденсатора как функцию времени, можно положить коэффициент затухания =0. Тогда, согласно выражению

w= ,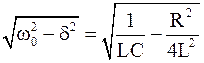

получим w₀=w. Следовательно, в контуре будут незатухающие колебания, при этом

q=q₀sin(wt+₀), (2)

Сила тока есть производная от заряда по времени. Поэтому, дифференцируя обе части (2) по времени, получим для силы тока в контуре уравнение

I=w₀q₀.cos(wt+₀).

Величина I₀=w₀.q₀ является амплитудным, т.е. максимальным, значением тока в контуре. Подставив w₀= 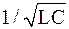и учитывая соотношение q₀=CU₀, определим искомую величину:

I₀=w₀q₀=C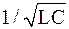U₀ =U₀. .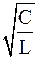

2. В процессе незатухающих электромагнитных колебаний полная электромагнитная энергия контура, равная сумме энергий электрического поля конденсатора W_С=CU²/2 и магнитного поля катушки W_L=LI²/2, остается величиной постоянной: W=W_С+W_L=const. При этом в те моменты, когда конденсатор максимально заряжен (U=U₀), сила тока равна нулю. Следовательно, полная энергия контура

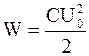. (3)

В момент полной зарядки (U=0), сила тока в контуре достигает максимального значения I₀. Тогда полная энергия равна

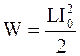. (4)

Приравняв правые части формул (3), (4), найдем

.

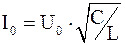Подставив значения величин, выраженные в единицах СИ, и произведя вычисления, получим I₀=0,45 А.

Ответ: I₀=0,45 А.

6.5.2. Добротность колебательного контура Q=5,0. Определить, на сколько процентов отличается частота w свободных колебаний контура от его собственной частоты w₀?

Решение. Во всяком реальном контуре, обладающим сопротивлением R, частота свободных электромагнитных колебаний w меньше собственной частоты контура w₀ (т.е. частоты колебаний при R®0). В задаче требуется найти величину x=(w₀ – w)/w₀=1 – w/w₀. (1)

Добротность контура выразим через величины w, w₀, используя формулы

; ;

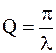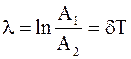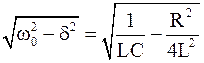
и соотношение T=2p/w, откуда имеем

Q=p/=p/T=w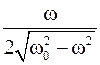/2= . (2)

Введя обозначения a=w/w₀, из (2) получим

.

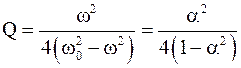Определив отсюда величину a, на основании (1) найдем

x=1 – a=1 – 2Q/(1+4Q²)^1/2. (3)

Переходя к вычислениям, учтем, что в данном случае 4Q²>>1. Поэтому формулу (3) можно упростить. Разделив числитель и знаменатель на 2Q и применив формулы приближенного вычисления, получим

x=1 – 1/(1+4Q²)^1/2 ~ 1 – 1/(1+8Q²) ~ 1 – (1 – 1/8Q²)=1/8Q².

Подставив значение Q, произведем вычисления

x=0,5010^-2, или x=0,50 %.

Ответ: x=0,50 %.

6.5.3. В цепи, состоящей из последовательно соединенных резистора сопротивлением R=20 Ом, катушки индуктивностью L=1,0 мГн и конденсатора емкостью C=0,10 мкФ, действует синусоидальная ЭДС Определить частоту w ЭДС, при которой в цепи наступит резонанс. Найти также действующее значение силы тока I и напряжений U_R, U_L, U_C на всех элементах цепи при резонансе, если при этом действующее значение ЭДС E= 30 В.

Решение. Под действием переменной ЭДС в данной цепи, представляющей собой колебательный контур, установятся вынужденные электромагнитные колебания. При этом амплитудные значения I₀ и ЭДС E₀ связаны соотношением

.

Из формул I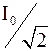_д= ; E_д= 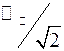видно, что между действующими значениями тока I_д и ЭДС E_д существует то же соотношение, что и между величинами I₀, E₀. Поэтому (опуская для простоты индексы у величин I_д, E_д) запишем

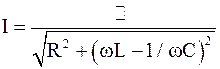. (1)

Очевидно, максимальному току при резонансе I_рез соответствует такое значение w, при котором в формуле (1) выражение (Lw – 1/Cw)²=0. Отсюда определяем резонансную частоту:

w=w_рез=[1/(LC)]^1/2=1,010⁵ рад/с. (2)

При этом сила тока равна

I_рез=E/R=1,5 А.

Зная силу тока I_рез, найдем действующие значения напряжения на каждом из элементов контура R, L, C, применив закон Ома для каждого из участков

U_R=I_резR=E=30 В;

U_L=I_резLw=ELw/R=150 В;

UC=I_рез[1/(wC)]=U_L=150 В.

Равенство U_L=U_C следует из равенства емкостного и индуктивного сопротивлений при резонансе.

Ответ: w_рез=1,010⁵ рад/с; I_рез=1,5 А; U_R=30 В; U_L=150 В; U_C=150 В.

6.5.4. Определить действующее значения силы тока на всех участках цепи, состоящей из параллельно включенных C, R, L и E, если R=1,0 Ом, L=1,0 мГн, C=0,110 мкФ, E=30 В, w=1,0010⁵ рад/с.

Решение. Эта цепь отличается от предыдущей способом включения источника переменной ЭДС (внутренним сопротивлением которого мы пренебрегаем). Если раньше все элементы цепи были включены последовательно, то в данном случае имеем разветвленную цепь переменного тока, одна из ветвей которого является параллельным соединением двух ветвей: конденсатора C и элементов R, L, соединенных последовательно между собой. Каждая из ветвей вместе с источником ЭДС образует колебательный (неполный) контур. Поэтому силу тока в каждой ветви снова найдем по формуле

,

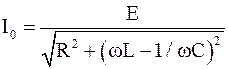заменив амплитудные значения величин I₀, ε₀ их действующими значениями I, E. Тогда для силы тока в ветви, состоящей из конденсатора C, где R=0, L=0, получим

I_C=ECw=0,33 А. (1)

В ветви R-L, где отсутствует емкостное сопротивление RC=1/(wC), сила тока с учетом того, что R²<<(Lw)² равна

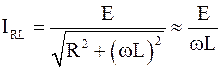=0,30 А. (2)

Если бы переменные токи в обеих ветвях имели одинаковые фазы, то сила тока в неразветвленной части цепи была бы равна сумме сил токов I_C, I_RL. Однако эти токи имеют различные фазы: между каждым из них и ЭДС E существует сдиг фаз, определяемый формулой

.

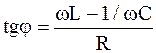Применим эту формулу для каждой ветви. Для ветви с конденсатором C: R=0, L=0.

Следовательно,

tg_C ® -¥; _C=-p/2.

Для ветви R-L, учитывая, что 1/(wC)=0, получим

tg_RL=Lw/R=100; _RL ~ p/2.

В формуле I=I₀sin(wt-) величина  стоит со знаком "-"; это означает, что ток I_C опережает по фазе ЭДС E на p/2, а ток I_RL отстает по фазе от ЭДС E на p/2. В связи с этим, ток в неразветвленной цепи

I=I_C – I_RL=0,03 А. (3)

Замечание. В данной задаче величины R, L, w были связаны соотношением R<<Lw. Именно поэтому переменные токи в параллельных ветвях

оказались в противоположных фазах (D ~ p). Если при этом величины w,C, L оказались бы связанными соотношением w=w_рез=[1/(LC)]^1/2, то, как видно из формул (1), (2), величины I_C, I_RL приблизительно одинаковы и согласно формуле (3), I=I_C-I_RL ~ 0. Точнее, при R ® 0, I ® 0 и, следовательно, полное сопротивление переменному току всего участка стремится к бесконечности. В этом случае наблюдается резонанс токов (в отличие от резонанса напряжений, рассмотренного в предыдущей задаче). Таким образом, при наличии неравенства R<<Lw условие резонанса токов совпадает с условием резонанса напряжений.

6.5.5. Два параллельных провода, погруженные в бензол, индуктивно соединены с генератором высокочастотных электромагнитных колебаний. При частоте n=100МГц в системе устанавливаются стоячие электромагнитные волны. Перемещая вдоль проводов газоразрядную трубку А, по ее свечению определяют положения пучностей напряженности электрического поля. Расстояние между соседними пучностями оказалось равным l=1,00 м. Найти диэлектрическую проницаемость бензола.

Решение. Стоячие электромагнитные волны возникают в результате интерференции волн, распространяющихся по двухпроводной линии от генератора в прямом направлении, с волнами, отраженными от конца линии. Учтем, что при данной высокой частоте электромагнитных колебаний основные процессы, связанные с распространением электромагнитных волн вдоль линии, происходят не в проводах, а в окружающей их среде (в следствие скин-эффекта переменный ток частоты n=10⁸ Гц течет практически лишь по поверхности проводов).

Согласно теории Максвелла, скорость электромагнитных волн в среде связана с их скоростью в вакууме формулой:

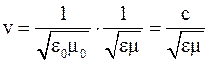, (1)

где c =3,0010⁸ м/с – скорость распространения электромагнитных волн(света) в вакууме.

Из формулы (1), учитывая, что для бензола  ~ 1, найдем его диэлектрическую проницаемость

e=c²/v². (2)

Скорость электромагнитных волн связана с длиной волны  и частотой n соотношением v=n. Поскольку расстояние между соседними пучностями в стоячей волне равно половине длины волны, т.е. =2l, то получим

e=c²/v²=c²/(4l²n²). (3)

Подставив числовые значения величин, выраженные в единицах СИ, и выполнив вычисление, найдем e= 2,2.

Ответ: e=2,2.

Пример 5. Колебательный контур состоит из катушки с индуктивностью L= 1,2 мГн и конденсатора переменной электроемкости от C₁=12 пФ до С₂=80 пФ. Определить диапазон длин электромагнитных волн, которые могут вызывать резонанс в этом контуре. Активное сопротивление контура принять равным нулю.

Решение. Длина λ электромагнитной волны, которая может вызвать резонанс в колебательном контуре, связана с периодом Т колебаний контура соотношением

λ =сТ. (1)

Период колебаний, в свою очередь, связан с индуктивностью L катушки и электроемкостью С конденсатора колебательного контура соотношением (формула Томсона) 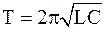. Следовательно,

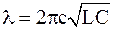. (2)

Согласно условию задачи, индуктивность контура неизменна, а электроемкость контура может изменяться в пределах от C₁ до C₂. Этим значениям электроемкости соответствуют длины волн λ₁ и λ₂,, определяющие диапазон длин волн, которые могут вызвать резонанс. После вычислений по формуле (2) получим:

λ₁=226м; λ₂=585 м.

6.5.6. Определить энергию, которую переносит за время t=1,00 мин плоская синусоидальная электромагнитная волна, распространяющаяся в вакууме, через площадку S=10,0 см², расположенную перпендикулярно направлению распространения волны. Амплитуда напряженности электрического поля волны E₀==1,00 мВ/м. Период волны T<<t.

Решение. Энергия переносимая электромагнитной волной за единицу времени через единицу поверхности, перпендикулярной направлению распространения волны, определяется вектором Пойнтинга P =[ EH ]. Учитывая, что в электромагнитной волне векторы E, H взаимно перпендикулярны и перпендикулярны направлению распространения волны, получим для модуля вектора P

P=EH. (1)

Поскольку обе величины E, H, характеризующие электромагнитную волну, в каждой ее точке меняются во времени по закону синуса, находясь в одинаковых фазах, соотношение (1) можно записать так:

P=E₀sinwtH₀sinwt=E₀H₀sin²wt. (2)

Таким образом, величина P является функцией времени, и формулы (1), (2) дают лишь мгновенное значение величины P. Поэтому, согласно определению вектора плотности потока энергии, запишем

.

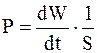Отсюда энергия dW, переносимая волной через площадку S за время dt, с учетом формулы (2), равна

dW=PdS=E₀H₀Ssin²(wt)dt. (3)

Здесь неизвестна величина H₀. Воспользуемся тем, что между величинами E, и H, характеризующими электромагнитную волну в одной и той же точке, существует простое соотношение. Найдем его, учитывая, что, согласно теории электромагнитных волн, плотности энергии электрического и магнитного полей волны в любой момент времени равны, т.е.

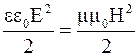. (4)

Так как, по условию, e==1, то из (4) получим

H=E(e₀/₀)^1/2.

Так же связаны между собой и амплитудные значения E₀, H₀. Тогда уравнение (3) примет вид

dW=(e₀/₀)^1/2E₀²Ssin²(wt)dt.

После интегрирования, с учётом того, что в силу неравенства T<<t членом sin(2wt)/4w можно пренебречь, получим

.

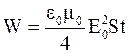Подставив числовые значения величин, выраженные в единицах СИ, и выполнив вычисления, найдем

W=8,010^-11 Дж.

Ответ: W=8,010^-11 Дж.