
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач
5.1.1. Пучок электронов влетает со скоростью vo=3,0106 м/с в плоский горизонтальный конденсатор параллельно его пластинам длиной 5,0010-2 м. Напряженность электрического поля конденсатора E=200 В/м. Определить угол отклонения пучка в результате его похождения через конденсатор.
Решение. Обычно заряженная частица, движущаяся в электромагнитном поле, находится также и в гравитационном поле (например, Земли). Поэтому кроме силы F =q E +q[ vB ], на частицу массы m действует также сила тяготения
Fг =m G,
где G – напряженность гравитационного поля.
Однако, как показывает расчет, для электронов, протонов и других заряженных микрочастиц, движущихся даже в слабых электрических и магнитных полях, величиной Fг можно пренебречь.
Поэтому, в рассматриваемом случае, на каждый электрон, обладающий зарядом e, во время его движения в электрическом поле конденсатора действует постоянная сила F= e E, направленная вдоль силовых линий (так как заряд электрона отрицательный, то направление этой силы противоположно направлению силовых линий вектора E), сообщающая электрону ускорение в ту же сторону
a=F /m=e E /m. (1)
В связи с чем, имея начальную горизонтальную скорость vo, он начинает двигаться по параболе с вершиной в точке А (в начальной точке электрического поля конденсатора). Выйдя из поля конденсатора, электрон снова будет двигаться прямолинейно под углом a к скорости vo. При этом
tga=v'/v0, (2)
где a – искомый угол;
v' – вертикальная составляющая скорости, приобретенная электроном под действием силы F;
v0 – начальная скорость электрона.
Учитывая, что по вертикали электрон движется ускоренно без начальной скорости, а по горизонтали – равномерно со скоростью vo, найдем по известным формулам кинематики
v'=at=al/v0. (3)
Теперь с учетом (3) и (1) перепишем формулу (2)
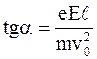 .
.
Взяв из справочных таблиц значения заряда и массы электрона, подставив в последнюю формулу числовые значения величин, выраженные в единицах СИ, выполнив вычисление, получим
tga=0,19; a=110.
Ответ: tga=0,19; a=110.
5.1.2. Пучок электронов влетает со скоростью v0 (v0<<c) в однородное магнитное поле перпендикулярно линиям магнитной индукции B. Определить угол a отклонения пучка магнитным полем, если занятая им область представляет собой в сечении плоскость, нормальную к силовым линиям магнитного поля; траектория движения электрона – окружность радиуса r0, а скорость v0 направлена по диаметру этой окружности.
Решение. Выясним характер движения электронов в магнитном поле. На влетевший в магнитное поле электрон действует сила Лоренца
F= [ v0B ]. (1)
Так как сила F нормальна к скорости v, она изменяет лишь направление вектора скорости, но не его модуль, т.е. сообщает электрону только нормальное ускорение. При этом вектор скорости остается перпендикулярным вектору B. Следовательно, сила F, определяемая по (1), сохраняет свое численное значение, сообщая электрону постоянное по модулю нормальное ускорение. Это значит, что электрон движется в магнитном поле по дуге окружности. Пусть r – радиус дуги (траектории движения электрона в магнитном поле). Из геометрических построений (если выполнить чертеж), искомый угол a определяется соотношением
tga=r0/r, (2)
где r0 – радиус окружности, по которой он сделал бы в магнитном поле один полный оборот.
Чтобы найти величину r, запишем уравнение движения электрона в магнитном поле, используя второй закон Ньютона. Посколькувекторы v и B перпендикулярны друг другу, то уравнение (1) можно записать в скалярной форме так
F=ev0B,
или, используя формулу нормального ускорения,
ev0B= 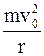 r.
r.
Отсюда получим
r=mv0/eB. (3)
Подставив это значение r в (2), найдем
a=2 arctg(r0eB/mv0).
5.1.3. Однородное магнитное поле, индукция которого B=10,0 мТл, направлено перпендикулярно однородному электрическому полю напряженностью E==17 кВ/м. Ион, пройдя ускоряющую разность потенциалов U=15 кВ и влетев в область, занятую полями, со скоростью, перпендикулярной обеим полям, движется равномерно и прямолинейно. Определить отношение q/m для этого иона.
Решение. В данном случае ион можно рассматривать как классическую частицу по следующим соображениям. Так как заряд иона одного порядка с зарядом электрона, то заведомо qU<<0,51 МэВ, т.е. кинетическая энергия иона пренебрежимо мала по сравнению с энергией покоя электрона. Тем более можно пренебречь этой величиной по сравнению с энергией покоя самого иона, пологая, таким образом, частицу классической.
Прежде чем попасть в область, занятую обоими полями, ион двигался ускоренно. Силы электрического поля, совершают работу над ионом, определяемую соотношением A=– DW=q(1 – 2),
при этом его кинетическая энергия увеличивается. Полагая начальную кинетическую энергию иона равной нулю, запишем
qU=mv2/2.
Отсюда получим
q/m=v2/2U. (1)
Теперь задача сводится к определению скорости движения иона в области, занятой электрическим и магнитным полями. Из характера этого движения следует, что действующая на ион сила F равна нулю
F= q E+ q[ vB ]=0.
Следовательно, взаимная ориентация и модули трех векторов v, B, E в данном случае таковы, что электрическая Fэл и магнитная Fм силы, действующие на ион, уравновешиваются. Отсюда, учитывая, что sina=1 (a – угол между векторами v, B), запишем скалярное уравнение:
qE=qvB. (2)
Исключив из уравнений (1), (2) величину v, получим:
q/m= 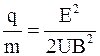 . (3)
. (3)
Подставив в формулу (3) числовые значения величин, выраженные в единицах системы СИ, и выполнив вычисление, получим
q/m=1,0108 Кл/кг.
Ответ: q/m=1,07108 Кл/кг.
Пример 2. Электрон, имея скорость u=2 Мм/с, влетел воднородное магнитное поле с индукцией В=30 мТл под углом a=30° к направлению линий индукции. Определить радиус Rи шаг hвинтовой линии, покоторой будет двигаться электрон.
Решение. Известно, что на заряженную частицу, влетевшую в магнитное поле, действует сила Лоренца, перпендикулярная векторам магнитной индукции В и скорости v частицы:
F=QuB sin a, (1)
где Q — заряд частицы.
В случае, если частицей является электрон, формулу (1) можно записать в виде
F= |e|uB sin a.
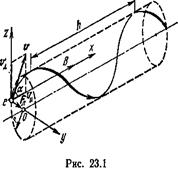 Так как вектор силы Лоренца перпендикулярен вектору скорости, то модуль скорости не будет изменяться под действием этой силы. Но при постоянной скорости, как это следует из формулы (1), останется постоянным и значение силы Лоренца. Из механики известно, что постоянная сила, перпендикулярная скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле, будет двигаться по окружности в плоскости, перпендикулярной линиям индукции, со скоростью, равной поперечной составляющей u1 скорости (рис. 23.1); одновременно он будет двигаться и вдоль поля со скоростью u||:
Так как вектор силы Лоренца перпендикулярен вектору скорости, то модуль скорости не будет изменяться под действием этой силы. Но при постоянной скорости, как это следует из формулы (1), останется постоянным и значение силы Лоренца. Из механики известно, что постоянная сила, перпендикулярная скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле, будет двигаться по окружности в плоскости, перпендикулярной линиям индукции, со скоростью, равной поперечной составляющей u1 скорости (рис. 23.1); одновременно он будет двигаться и вдоль поля со скоростью u||:
u|| = u sin a, u|| = u cos a.
В результате одновременного участия в движениях по окружности и по прямой электрон будет двигаться по винтовой линии.
Радиус окружности, по которой движется электрон, найдем следующим образом. Сила Лоренца F сообщает электрону нормальное ускорение ап. По второму закону Ньютона, F=man, где F=|e|u1B и an=u2 ^R,. Тогда
|e|u^B = mu22/R,
откуда после сокращения на uz находим радиус винтовой линии:

Подставив значения величин т, u, e, В и a и произведя вычисления, получим
R=0,19 мм.
Шаг винтовой линии равен пути, пройденному электроном вдоль поля со скоростью ux за время, которое понадобится электрону для того, чтобы совершить один оборот,
h =u|| T (2)
где T=2pR/u^— период вращения электрона. Подставив это выражение для Т в формулу (2), найдем
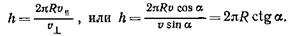
Подставив в эту формулу значения величин p, R и a и вычислив, получим
h=2,06 мм.
5.1.4. Электрон влетает со скоростью v0=1,00107 м/с в плоский горизонтальный конденсатор параллельно его пластинам, длина которых l==5,0 см. Напряженность электрического поля конденсатора E=10,0 кВ/м. При вылете из него электрон попал в однородное магнитное поле, направленное вдоль вектора vo. Магнитная индукция этого поля B=15 мТл. Определить траекторию электрона в магнитном поле.
Решение. Обычно заряженная частица, движущаяся в электромагнитном поле, находится также и в гравитационном поле (например, Земли). Поэтому кроме силы F =q E +q[ vB ], на частицу массы m действует также сила тяготения
Fг =m G,
где G – напряженность гравитационного поля.
Однако, как показывает расчет, для электронов, протонов и других заряженных микрочастиц, движущихся даже в слабых электрических и магнитных полях, величиной Fг можно пренебречь.
Поэтому, в рассматриваемом случае, на каждый электрон, обладающий зарядом e, во время его движения в электрическом поле конденсатора действует постоянная сила F =e E, направленная вдоль силовых линий (так как заряд электрона отрицательный, то направление этой силы противоположно направлению силовых линий вектора E), сообщающая электрону ускорение в ту же сторону
a=F /m=e E /m.
В связи с чем, имея начальную горизонтальную скорость vo, он начинает двигаться по параболе с вершиной в точке А (в начальной точке электрического поля конденсатора). Выйдя из поля конденсатора, электрон снова будет двигаться прямолинейно под углом a к скорости v0. При этом по вертикали электрон движется ускоренно без начальной скорости, а по горизонтали – равномерно со скоростью vo. Скорость электрона по вертикали найдем по известным формулам кинематики
v'=at=al/vo=eEl/mv0. (1)
При вылете из конденсатора скоростьэлектрона v0 направлена вдоль линий индукции магнитного поля B, а скорость v' – перпендикулярна им.
Когда электрон попадает в магнитное поле, на него действует сила Лоренца, равная Fм =q[ vB ] или, с учетом условия задачи, в скалярной форме, эта сила будет равна
Fм=qv'B.
Если бы электрон обладал только скоростью v', то под действие силы Лоренца он двигался бы по окружности, радиус которой равен:
r=mv'/eB=El/v0B. (2)
Так как у электрона есть еще и скорость v0, перпендикулярная плоскости этой окружности, он будет двигаться по винтовой линии, характеризуемой радиусом и шагом. Радиус винтовой линии определяется формулой (2). Шаг винтовой линии представляет собой то расстояние, на которое переместится электрон, двигаясь равномерно со скоростью v0 за время, в течение которого он совершит один полный оборот, т.е. за время одного периода. Период Т с учетом соотношения (2) равен
Т=2pr/v'=2pm/eB.
Следовательно, шаг винтовой линии
h=v0T=2pmvo/eB. (3)
Выразив величины в единицах системы СИ, входящие в формулы (2), (3), подставив их значения и выполнив вычисление, получим:
r=3,310-3 м; h=2,410-2 м.
Ответ: r=3,310-3 м; h=2,410-2 м.
5.1.5. Какую ускоряющую разность потенциалов должен пройти электрон, чтобы приобрести скорость, равную 0,90 с?
Решение. Силы электрического поля, перемещая электрон (заряженную частицу), совершают работу, определяемую по формуле:
A=q(1 – 2)=qU.
Пологая начальную кинетическую энергию частицы равной нулю, можно утверждать, что работа сил электрического поля равна кинетической энергии, приобретенной электроном, когда он пройдет искомую разность потенциалов, т.е. A=T, или T=eU, откуда
U=T/e. (1)
Так как в данном случае скорость частицы (электрона) близка к скорости света в вакууме, то классическое выражение кинетической энергии Т=mv2/2, необходимо заменить релятивистским:
T=W – Wo, (2)
где T – кинетическая энергия релятивистской частицы;
W = mc2 – полная энергия релятивистской частицы;
W0=m0c2 – энергия покоя релятивистской частицы;
m – масса движущейся релятивистской частицы;
m0 – масса покоя релятивистской частицы;
c – скорость света в вакууме;
=v/c;
v – скорость релятивистской частицы.
Масса движущейся релятивистской частицы связана со скоростью ее движения v соотношением
 . (3)
. (3)
С учетом (3) формула (2) будет записана так
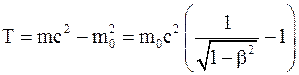 . (4)
. (4)
Подставив в (1) вместо T ее значение по (4), будем иметь
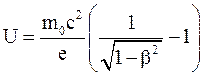 (5)
(5)
Выразив величины в единицах системы СИ, входящие в формулу (5), подставив их значения и выполнив вычисление, получим:
U=6,6105 В=0,66 МВ.
Ответ: U=6,67105 В=0,66 МВ.
5.1.6. Электрон движется в однородном магнитном поле с индукцией B==5,010-2 Тл по окружности радиуса r=4,010-2 м. Определить кинетическую энергию электрона.
Решение. Чтобы определить кинетическую энергию частицы (независимо от того, является ли она классической или релятивистской), необходимо знать ее массу покоя m0 и скорость v или массу m0 и импульс p. Так как масса покоя электрона – величина известная, задача сводится к определению скорости или импульса электрона. Для этого запишем уравнение движения электрона в магнитном поле, т.е. второй закон Ньютона. Учитывая зависимость массы частицы от скорости, этот закон следует записать в форме: d p /dt= 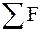 .
.
Но, так как при движении электрона в магнитном поле действующая на него сила Лоренца все время перпендикулярна вектору скорости v, модуль скорости не изменяется. Следовательно, остается постоянной во время движения и масса частицы. Поэтому в данном случае независимо от того, классической или релятивистской является частица, второй закон Ньютона может быть записан так
m a= 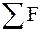 .
.
С учетом условия задачи (в однородном магнитном поле электрон движется по окружности): 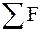 =Fл=
=Fл= 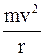 =evB. Отсюда найдем импульс электрона
=evB. Отсюда найдем импульс электрона
p=mv=evB. (1)
Теперь, чтобы выразить кинетическую энергию электрона T через его импульс p, необходимо выяснить: классической или релятивистской частицей следует считать электрон в условиях данной задачи, так как в этих двух случаях зависимость между величинами p и T различна. Для этого вычислим импульс p по формуле (1)
p=1,610-195,010-24,010-2=3,210-22 кгм/с.
Вместе с тем комптоновский импульс электрона равен
p=m0c=9,110-313,0108=2,7310-22 кгм/с.
Из полученных результатов видно, что неравенство p<<m0c, необходимое для того, чтобы частицу можно было считать классической, в данной задаче не выполняется, следовательно, необходимо пользоваться релятивистскими формулами
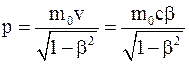 ;
;
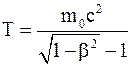 .
.
Исключив из них величину , найдем
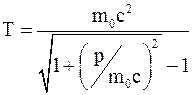 . (2)
. (2)
Так как для электрона m0c2=0,51 МэВ, а величины p, m0c уже вычислены, то по формуле (2) получим
T=0,28 МэВ.
Ответ: T=0,28 МэВ.
5.1.7. Радиус орбиты электронов, ускоряемых бетатроном, r=300 мм. Среднее по площади орбиты значение магнитной индукции Bср поля, создаваемого магнитом бетатрона, изменяясь со временем приблизительно по линейному закону, возрастает от нуля до B1=0,200 Тл. Определить скорость, приобретенную за это время электронами.
Решение. В магнитном поле бетатрона под действием лоренцевых сил электроны движутся по окружности. При изменении магнитного поля изменяется и магнитный поток Ф сквозь контур, совпадающий с орбитой электронов, что порождает вихревое электрическое поле. Так как электроны движутся вдоль одной из силовых линий электрического поля, то под действием последнего скорость их будет возрастать.
Напряженность E вихревого электрического поля в точках орбиты электронов найдем по закону электромагнитной индукции
E  ,
,
где контур интегрирования совпадает с одной из линий вектора E, имеющей форму окружности радиуса r. Поэтому EL=E=const для всех точек контура и, следовательно,
E 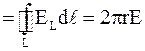 . (2)
. (2)
Так как магнитный поток изменяется равномерно в течение t от нуля до значения Фмакс, то скорость его изменения можно выразить так
dФ/dt=Фмакс/t=B1pr2/t. (3)
Из (1) – (3) получим для модуля вектора E
E=B1 r/2t.
Значит на каждый электрон, движущийся в магнитном поле по окружности, будет действовать со стороны вихревого электрического поля постоянная по модулю сила, равная
F=eE=eB1r/2t (4)
и направленная вдоль вектора скорости, а поэтому сообщающая электрону тангенциальное ускорение.
Чтобы найти скорость, приобретенную электроном в результате действия на него в течение времени t силы F, применим к нему второй закон Ньютона, записав его для касательного к траектории направления. Поскольку в бетатроне электроны разгоняются, как правило, до скоростей, близких к скорости света в вакууме, запишем уравнение движения электрона в виде
 .
.
Интегрируя это уравнение и принимая, что v=0 при t=0, найдем
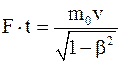 ,
,
откуда
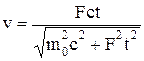 . (5)
. (5)
Наконец, подставив в уравнение (5) значение силы F из формулы (4), определим
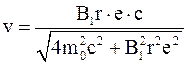 .
.
Выразив в единицах СИ величины, входящие в формулу, выполнив вычисление, получим: v=0,998 c.
Ответ: v=0,998 c.
Пример 1. Электрон, пройдя ускоряющую разность потенциалов U=400 В, попал воднородное магнитное поле с индукцией B=1,5 мТл. Определить: 1)радиус Rкривизны траектории; 2)частоту пвращения электрона вмагнитном поле. Вектор скорости электрона перпендикулярен линиям индукции.
Решение. 1. Радиус кривизны траектории электрона определим, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца F. (Действием силы тяжести можно пренебречь.) Вектор силы Лоренца перпендикулярен вектору скорости и, следовательно, по второму закону Ньютона, сообщает электрону нормальное ускорение аn : F=man. Подставив сюда выражения F и аn, получим
|e|vB sin a=mv2/R, (1)
где е, v, т — заряд, скорость, масса электрона; В — индукция магнитного поля; R — радиус кривизны траектории; a — угол между направлениями векторов скорости v и индукции В (в нашем случае v ^ B и a = 90°, sin a =l).
Из формулы (1) найдем
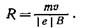 (2)
(2)
Входящий в выражение (2) импульс mu выразим через кинетическую энергию Т электрона:
 (3)
(3)
Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством Т= |e|U. Подставив это выражение Т в формулу (3), получим 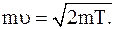
Тогда выражение (2) для радиуса кривизны приобретает вид
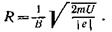
Убедимся в том, что правая часть этого равенства дает единицу длины (м):
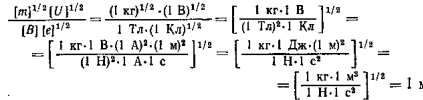
После вычисления по формуле (4) найдем
R=45 мм.
2. Для определения частоты вращения воспользуемся формулой связывающей частоту со скоростью и радиусом кривизны траектории,
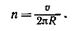
Подставив R из выражения (2) в эту формулу, получим

Произведя вычисления, найдем n=4,20 ∙ 107 c-1 .
5.1.8. Протон, прошедший ускоряющую разность потенциалов U=600 В, влетел в однородное магнитное поле с индукцией B=0,3 Тл и начал двигаться по окружности. Вычислить радиус R окружности.
Решение. Движение заряженной частицы в однородном магнитном поле будет происходить по окружности только в том случае, когда частица влетит в магнитное поле перпендикулярно линиям магнитного поля (направление скоростичастицы v перпендикулярно вектору индукции магнитного поля B). Так как сила Лоренца перпендикулярна вектору v, то она сообщит частице (протону) нормальное ускорение an.
Согласно второму закону Ньютона,
FЛ= m an, (1)
где m – масса протона.
Перепишем выражение (1) в скалярной форме (в проекции на радиус)
FЛ = man. (2)
В скалярной форме FЛ=qvBsina,
где a – угол между направлениями векторов v и B.
В нашем случае эти векторы перпендикулярны. Следовательно, sina=1, тогда FЛ=qvB.
Так как нормальное ускорение an=v2/R, то выражение (2) перепишем следующим образом: qvB=mv2/R.
Отсюда находим радиус окружности
R=mv/(qB).
Заметив, что mv=p – импульс протона, это выражение можно записать в виде
R=p/(qB). (3)
Импульс протона найдем, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е.
A=DT или q(1-2)=T2-T1,
где (1 – 2)=U – ускоряющая разность потенциалов (ускоряющее напряжение);
T1 и T2 – начальная и конечная кинетические энергии протона. Пренебрегая начальной кинетической энергией протона (T1 ~ 0) и выразив кинетическую энергию T2 через импульс p, получим
qU=p2/(2m).
Из этого выражения найдем импульс p= 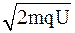 и подставим его в (3)
и подставим его в (3)
 . (4)
. (4)
Подставим в формулу (4) числовые значения физических величин, выраженные в единицах СИ, произведем вычисления
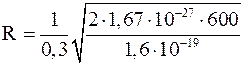 =1210-3 м.
=1210-3 м.
Ответ: R=1210-3 м=12 мм.
5.1.11. Альфа-частица прошла ускоряющую разность потенциалов U=104 В и влетела в скрещенные под прямым углом электрическое (E=10 кВ/м) и магнитное (B=0,1 Тл) поля. Найти отношение заряда альфа-частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.
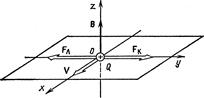
Решение. Для того чтобы найти отношение заряда q альфа-частицы к ее массе m, воспользуемся связью между работой сил электрического поля и изменением кинетической энергии частицы:
A=DWк, где A=qU; DWк=Wк2-Wк1=mv2/2,
Откуда
qU=mv2/2, а q/m=v2/(2U). (1)
Скорость v альфа-частицы найдем из следующих соображений. В скрещенных электрическом и магнитном полях на движущуюся заряженную частицу действуют две силы:
а) сила Лоренца FЛ =q[ vB ], направленная перпендикулярно скорости v и вектору магнитной индукции B;
б) кулоновская сила Fк= q E, сонаправленная с векторомнапряженности E электростатического поля (q > 0).
Альфа-частица не будет испытывать отклонения, если геометрическая сумма сил Fк+FЛ =0. В проекции на какую-либо ось получим следующее равенство (с учетом того, что v перпендикулярна B и sina=1)
qE-qvB=0,
откуда v=E/B.
Подставив это выражение скорости в формулу (1), получим
q/m=E2/(2UB2). (2)
Подставим в формулу (2) числовые значения физических величин, выраженные в единицах СИ, произведем вычисления:
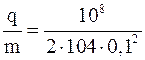 =4,8107 Кл/кг.
=4,8107 Кл/кг.
Ответ: q/m=4,8107 Кл/кг.
5.1.9. Электрон, влетев в однородное магнитное поле (B=0,2 Тл), стал двигаться по окружности радиуса R=5 см. Определить магнитный момент pm эквивалентного кругового тока.
Решение. Электрон начинает двигаться по окружности, если он влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции.
Движение электрона по окружности эквивалентно круговому току, который в данном случае определяется выражением
I=e/T,
где e – заряд электрона;
T – период его обращения.
Период обращения можно выразить через скорость электрона v и путь, проходимый электроном за период T=v/(2pR). Тогда
Iэкв=ev/(2pR). (1)
Зная Iэкв, найдем магнитный момент эквивалентного кругового тока. По определению, магнитный момент контура с током выражается соотношением
pm=IэквS, (2)
где S – площадь, ограниченная окружностью, описываемой электроном (S= pR2).
Подставив Iэкв из (1) в (2), получим
pm=evR/2. (3)
В полученном выражении известной является скорость электрона, которая связана с радиусом R окружности, по которой он движется, соотношением R==mv/(eB), откуда v=eBR/m. Тогда формула (3) примет вид
pm=e2BR2/(2m). (4)
Подставим в формулу (4) числовые значения физических величин, выраженные в единицах СИ, произведем вычисления
pm= 710-12 Ам2.
Ответ: pm=710-12 Ам2=7 пАм2.
Пример 3. Электрон движется воднородном магнитном поле с индукцией В=0,03 Тл поокружности радиусом r=10см. Определить скорость uэлектрона.
Решение. Движение электрона по окружности в однородном магнитном поле совершается под действием силы Лоренца (см. примеры 1 и 2). Поэтому можно написать
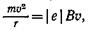 (1)
(1)
откуда найдем импульс электрона:
р=тu=|е|Вr. (2)
Релятивистский импульс выражается формулой

Выполнив преобразования, получим следующую формулу для определения скорости частицы:
 (3)
(3)
В данном случае р= |e|Br. Следовательно,
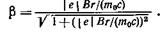
В числитель и знаменатель формулы (4) входит выражение |е| Вr(т0 с). Вычислим его отдельно:
|е| Вr / (m0c) = 1,76.
Подставив найденное значение отношения |е| Вr(т0 с) в формулу (4), получим
b = 0,871, или u = сb= 2,61-108 м/с.
Электрон, обладающий такой скоростью, является релятивистским (см. § 5).
5.1.10. Электрон движется в однородном магнитном поле (B=10 мТл) по винтовой линии, радиус которой R=1 см и шаг h=6 см. Определить период обращения электрона T и его скорость v.
Решение. Электрон будет двигаться по винтовой линии, если он влетает в однородное магнитное поле под некоторым углом (a – p/2) к линиям магнитной индукции. Разложим скорость v электрона на две составляющие: параллельную вектору B (v1) и перпендикулярную ему v2. Скорость v1 в магнитном поле не изменяется и обеспечивает перемещение электрона вдоль силовой линии. Скорость v2 в результате действия силы Лоренца изменяется только по направлению (сила Лоренца перпендикулярна скорости v2. В отсутствии составляющей v1 =0 движение электрона происходило бы по окружности в плоскости, перпендикулярной магнитным силовым линиям). Таким образом, электрон будет участвовать в дух движениях: равномерном перемещении со скоростью v1 и равномерном движении по окружности со скоростью v2.
Период обращения электрона связан с перпендикулярной составляющей скорости соотношением
T=2pR/v2. (1)
Найдем отношение R/v2. Для этого воспользуемся тем, что сила Лоренца сообщает электрону нормальное ускорение an= 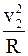 . Согласно второму закону Ньютона можно записать
. Согласно второму закону Ньютона можно записать
FЛ=man, или ev2B=  , (2)
, (2)
где v2=vsina.
Сделав соответствующие преобразования (2), выразив R/v2=m/(eB), подставив его в формулу (1), будем иметь
T=2pm/(eB). (3)
Модуль скорости v можно выразить через v1 и v2 следующим образом
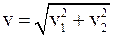 . (4)
. (4)
Из формулы (2) выразим перпендикулярную составляющую скорости
v2=eBR/m.
Параллельную составляющую скорости v1 найдем из следующих соображений. За время, равное периоду обращения T, электрон пройдет вдоль силовой линии расстояние, равное шагу винтовой линии, т.е. h=v1T, откуда
v1=h/T. (5)
Подставив вместо T правую часть выражения (2), получим
v1=eBh/(2pm). (6)
Таким образом, модуль скорости электрона
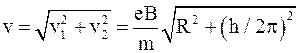 . (7)
. (7)
Подставим в формулы (3), (7) числовые значения физических величин, выраженные в единицах СИ, произведем вычисления:
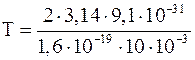 =3,610-9 с.
=3,610-9 с.
v= 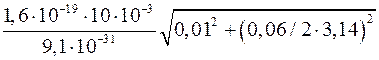 =2,5107 м/с.
=2,5107 м/с.
Ответ: T=3,610-9 с; v=2,5107 м/с.
Пример 2. Определим частоту ωL ларморовой прецессии электронной орбиты в атоме, находящемся в однородном магнитном поле (B=1 Тл).
Решение. Пусть электрон движется со скоростью v по круговой орбите радиусом r в направлении, указанном стрелкой на рис. 27.1. Момент импульса 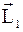 орбитального движения электрона в соответствии с правилом винта направлен перпендикулярно плоскости орбиты так, как это отмечено на рисунке.
орбитального движения электрона в соответствии с правилом винта направлен перпендикулярно плоскости орбиты так, как это отмечено на рисунке.
Орбитальный магнитный момент 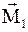 будет противонаправлен вектору
будет противонаправлен вектору 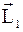 . Под действием внешнего магнитного поля (В), возбужденного вдоль оси Oz, на электронную орбиту будет действовать момент силы М =[
. Под действием внешнего магнитного поля (В), возбужденного вдоль оси Oz, на электронную орбиту будет действовать момент силы М =[ 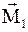 В ], направление которого перпендикулярно плоскости, содержащей векторы
В ], направление которого перпендикулярно плоскости, содержащей векторы 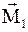 и В. Под действием этого момента вектор
и В. Под действием этого момента вектор 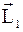 получит приращение d
получит приращение d 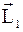 = M dt в направлении, совпадающем с М, в результате чего плоскость, содержащая векторы
= M dt в направлении, совпадающем с М, в результате чего плоскость, содержащая векторы 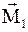 и В, повернется на угол dφ. Из рис. 27.1 видно, что
и В, повернется на угол dφ. Из рис. 27.1 видно, что
dφ= 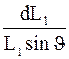 .
.
Тогда угловая скорость прецессии (ларморова частота)
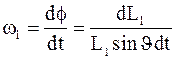
Так как dLl=Mdt, a M=Ml В sin 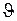 , то
, то 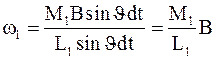 .
.
Воспользовавшись гиромагнитным отношением Ml/Ll= 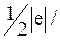 m, получим
m, получим
 .
.
Убедимся в том, что правая часть равенства дает единицу угловой скорости (с-1):

Произведем вычисления:
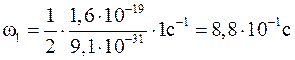
Date: 2015-09-18; view: 4523; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |