
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Зведення основних положень та результатів
1. Будь-яке просте скіченне поле ізоморфне 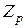 ‑ полю лишків за модулем
‑ полю лишків за модулем 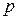 при деякому простому
при деякому простому 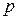 (операції в
(операції в 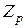 ‑ це операції над цілими числами за
‑ це операції над цілими числами за 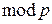 ).
).
2. Кожне скінченне поле містить просте підполе 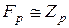 (при деякому простому
(при деякому простому 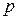 ), і тільки одне.
), і тільки одне.
3. Кожне скінченне поле має 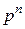 елементів, де
елементів, де  деяке просте, а
деяке просте, а 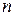 ‑ натуральне числа і позначається
‑ натуральне числа і позначається 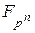 або
або 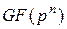 .
. 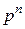 ‑ кількість елементів поля ‑ називається його порядком,
‑ кількість елементів поля ‑ називається його порядком, 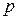 ‑ характеристикою поля, а
‑ характеристикою поля, а 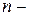 степенем розширення над простим підполем
степенем розширення над простим підполем 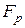 .
.
4. 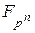 є лінійним векторним простором над
є лінійним векторним простором над 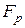 . Це означає, що елементи поля
. Це означає, що елементи поля 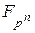 можна зобразити як вектори розмірності
можна зобразити як вектори розмірності 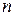 з компонентами з простого поля
з компонентами з простого поля 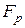 . Додавання цих елементів виконується покомпонентно – компоненти додаються за
. Додавання цих елементів виконується покомпонентно – компоненти додаються за 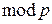 . Елементи
. Елементи 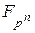 можна також зобразити як поліноми степеня не вище за
можна також зобразити як поліноми степеня не вище за 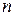 з коефіцієнтами з простого підполя. Множення в
з коефіцієнтами з простого підполя. Множення в 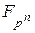 виконується як множення цих поліномів за
виконується як множення цих поліномів за 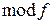 , де
, де 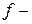 незвідний над
незвідний над 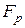 поліном степеня
поліном степеня 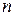 , причому поля, одержані за допомогою різних незвідних поліномів степеня
, причому поля, одержані за допомогою різних незвідних поліномів степеня 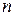 , ізоморфні.
, ізоморфні.
5. 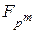 є підполем
є підполем 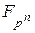 (інакше кажучи,
(інакше кажучи, 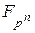 є розширенням
є розширенням 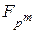 ) тоді і тільки тоді, коли
) тоді і тільки тоді, коли 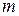 ділить
ділить 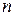 .
.
6. Нехай 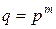 . Кожен елемент
. Кожен елемент 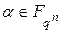 є алгебраїчним над
є алгебраїчним над 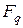 , тобто є коренем деякого полінома з коефіцієнтами з
, тобто є коренем деякого полінома з коефіцієнтами з 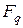 . Серед усіх поліномів над
. Серед усіх поліномів над 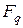 , для яких
, для яких 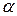 є коренем, існує єдиний незвідний нормований поліном. Він називається мінімальним поліномом елемента
є коренем, існує єдиний незвідний нормований поліном. Він називається мінімальним поліномом елемента 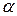 .
.
7. Множина ненульових елементів 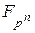 з операцією множення, заданою в цьому полі, утворює мультиплікативну групу скінченного поля. Ця група циклічна.
з операцією множення, заданою в цьому полі, утворює мультиплікативну групу скінченного поля. Ця група циклічна.
8. Твірні елементи мультиплікативної групи називаються примітивними елементами поля 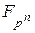 . Їх кількість дорівнює
. Їх кількість дорівнює 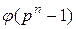 . Використовуючи зображення елементів скінченного поля як степенів примітивного елемента (таблицю індексів), зручно обчислювати добуток елементів
. Використовуючи зображення елементів скінченного поля як степенів примітивного елемента (таблицю індексів), зручно обчислювати добуток елементів 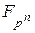 .
.
9. Всі елементи поля 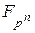 , і тільки вони, задовольняють рівності
, і тільки вони, задовольняють рівності 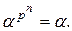 Нехай
Нехай 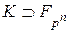 . Для того, щоб перевірити, чи належить полю
. Для того, щоб перевірити, чи належить полю 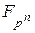 елемент
елемент 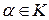 , досить перевірити для нього цю рівність. Інакше кажучи, всі елементи поля
, досить перевірити для нього цю рівність. Інакше кажучи, всі елементи поля 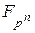 , і тільки вони, є коренями полінома
, і тільки вони, є коренями полінома 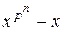 , а поле
, а поле 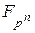 ‑ поле розкладу цього полінома.
‑ поле розкладу цього полінома.
10. Над полем 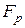 поліном
поліном 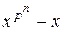 розкладається у добуток всіх незвідних над
розкладається у добуток всіх незвідних над 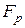 нормованих поліномів, степні яких ділять
нормованих поліномів, степні яких ділять 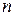 .
.
11. Корені незвідного над 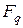 полінома
полінома 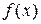 степеня
степеня 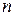 лежать у полі
лежать у полі 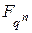 . Якщо
. Якщо 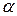 ‑ корінь
‑ корінь 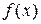 , то всі його корені можна зобразити у вигляді:
, то всі його корені можна зобразити у вигляді: 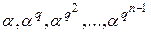 .
.
12. Незалежно від того, чи є 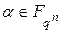 коренем незвідного полінома, елементи
коренем незвідного полінома, елементи 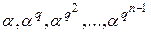 називаються спряженими з
називаються спряженими з 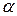 відносно поля
відносно поля 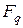 . Спряжені елементи (а отже і корені незвідного полінома) мають однаковий порядок у мультиплікативній групі поля
. Спряжені елементи (а отже і корені незвідного полінома) мають однаковий порядок у мультиплікативній групі поля 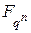 .
.
13. Сума всіх спряжених з 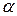
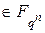 відносно
відносно 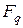 елементів називається слідом
елементів називається слідом 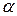 над
над 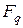 , а добуток – нормою. Слід є лінійним відображенням
, а добуток – нормою. Слід є лінійним відображенням 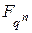
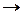
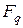 ; через слід виражаються всі лінійні відображення
; через слід виражаються всі лінійні відображення 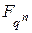 в
в 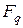 .
.
14. 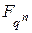 , як лінійний векторний простір над
, як лінійний векторний простір над 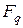 , має базис розмірності
, має базис розмірності 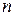 . Базис, що складається з степенів
. Базис, що складається з степенів 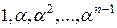 , де
, де 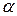 ‑ корінь деякого незвідного над
‑ корінь деякого незвідного над 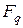 полінома степеня
полінома степеня 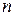 , називається поліноміальним. Якщо базис складається із спряжених над
, називається поліноміальним. Якщо базис складається із спряжених над 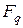 елементів, то він називається нормальним. Для будь-якого скінченного поля існує нормальний базис над будь-яким його підполем.
елементів, то він називається нормальним. Для будь-якого скінченного поля існує нормальний базис над будь-яким його підполем.
15. Порядком полінома 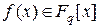 (
(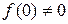 ) називається мінімальне натуральне число
) називається мінімальне натуральне число  таке, що
таке, що 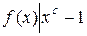 (таке
(таке  завжди існує) і позначається
завжди існує) і позначається 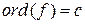 . Якщо
. Якщо 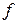 ‑ незвідний поліном степеня
‑ незвідний поліном степеня 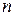 , то
, то 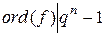 ; для звідного полінома це, взагалі кажучи, не так. Найбільший порядок, який може мати поліном степеня
; для звідного полінома це, взагалі кажучи, не так. Найбільший порядок, який може мати поліном степеня 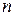 над
над 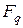 , дорівнює
, дорівнює 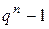 .
.
16. Порядки довільних поліномів через порядки незвідних поліномів обчислюються наступним чином. Нехай 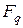 – скінченне поле характеристики p,
– скінченне поле характеристики p, 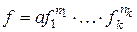 – канонічний розклад полінома
– канонічний розклад полінома 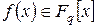 ,
, 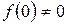 ,deg
,deg 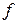 >0. Тоді
>0. Тоді
a. 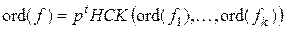 ,
,
b. де 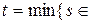 N
N 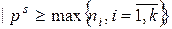 .
.
17. Незвідний нормований поліном 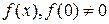 степеня
степеня 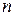 , який має порядок
, який має порядок 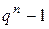 , називається примітивним. Він є мінімальним поліномом деякого примітивного елемента поля
, називається примітивним. Він є мінімальним поліномом деякого примітивного елемента поля 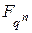 ; більше того, всі корені примітивного полінома ‑ примітивні. Кількість примітивних поліномів степеня
; більше того, всі корені примітивного полінома ‑ примітивні. Кількість примітивних поліномів степеня 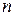 над
над 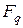 дорінює
дорінює 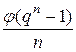 .
.
18. Автоморфізм скінченного поля 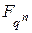 над підполем
над підполем 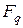 ‑ це автоморфізм
‑ це автоморфізм 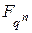 , який залишає елементи
, який залишає елементи 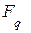 на місці. Всі автоморфізми
на місці. Всі автоморфізми 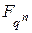 над
над 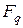 вичерпуються відображеннями виду:
вичерпуються відображеннями виду: 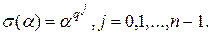
ПРЕДМЕТНИЙ ПОКАЖЧИК
| автоморфізм 5 ‑‑ поля над підполем 44 алгоритм Евкліда 8 базис поля над підполем 20, 42 ‑‑ ‑‑ автодуальний 42 ‑‑ ‑‑ дуальний 42 ‑‑ ‑‑ нормальний 43 ‑‑ ‑‑ поліноміальний 42 башта розширень 20 гомоморфізм 5 група 4 ‑‑ абелева 4 ‑‑ адитивна 4 ‑‑ мультиплікативна 4 ‑‑ ‑‑ скінченного поля 27 ‑‑ нескінченна 4 ‑‑ скінченна 4 ‑‑ циклічна 4 експонента полінома 35 елемент алгебраїчний 21 ‑‑ обернений до 7 ‑‑ оборотний 7 ‑‑ примітивний 28 ‑‑ спряжений 31 ‑‑ твірний (циклічної групи) 5 ендоморфізм 4 епіморфізм 5 зображення елементів скінченних полів 32 значення полінома 10 ідеал 6 ‑‑ головний 6 ізоморфізм 5 поле 7 ‑‑ Галуа 20 ‑‑ просте 19 ‑‑ розкладу полінома 25 -- часток 16 подільність поліномів 11 поліном мінімальний 22 ‑‑ над кільцем 10 ‑‑ над полем 11 ‑‑ незвідний 13 ‑‑ нормований 12 ‑‑ нульовий 10 ‑‑ примітивний 38 ‑‑ характеристичний елемента порядок групи 4 ‑‑ полінома 35 ‑‑ поля 20 похідна полінома 16 простір лінійний векторний 20 рівність поліномів 10 розширення поля 19 ‑‑ ‑‑ алгебраїчне 21 ‑‑ ‑‑ одержане шляхом приєднання елементів 19 ‑‑ ‑‑ просте 19 ‑‑ ‑‑ скінченне 20 слід 39 ‑‑ абсолютний 39 степінь полінома 10 ‑‑ розширення 20 структура алгебраїчна 4 |
індекс 34
кільце 5
‑‑ головних ідеалів 6
‑‑ евклідове 5
‑‑ з одиницею 5
‑‑ комутативне 5
‑‑ лишків за 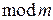 7
‑‑ поліномів над кільцем 10
‑‑ ‑‑ ‑‑ полем 11
‑‑ цілих чисел 6, 7
‑‑ цілісне 5
коефіцієнт полінома 10
‑‑ ‑‑ старший 10
корінь полінома 15
‑‑ ‑‑ кратності 7
‑‑ поліномів над кільцем 10
‑‑ ‑‑ ‑‑ полем 11
‑‑ цілих чисел 6, 7
‑‑ цілісне 5
коефіцієнт полінома 10
‑‑ ‑‑ старший 10
корінь полінома 15
‑‑ ‑‑ кратності 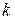 15
‑‑ ‑‑ незвідного 29
‑‑ ‑‑ простий 15
мономорфізм 5
напівгрупа 4
найбільший спільний дільник
чисел 8
‑‑ ‑‑ ‑‑ поліномів 12
найменше спільне кратне
поліномів 12
норма 41
носій алгебраїчної структури 4
область цілісності 5
операція бінарна 4
період полінома 35
підгрупа 5
підкільце 6
підполе 17
‑‑ власне 17
таблиця індексів 34
теорема Безу 15
‑‑ Лагранжа 5
‑‑ про автоморфізми
скінченних полів 44
‑‑ -- “башту” розширень 20
‑‑ ‑‑ властивості норми 41
‑‑ ‑‑ властивості сліду 39
‑‑ ‑‑ гомоморфізм кілець 7
‑‑ ‑‑ існування та єдиність
скінченних полів 25
‑‑ ‑‑ канонічний розклад
полінома 13
‑‑ критерій підполя 26
‑‑ про мультиплікативну групу
скінченного поля 27
‑‑ ‑‑ нормальний базис 43
‑‑ ‑‑ степені поліномів 10
‑‑ ‑‑ транзитивність сліду 41
характеристика поля 18
фактор-кільце 6
‑‑ ‑‑ поліномів 13
ядро гомоморфізму 7 15
‑‑ ‑‑ незвідного 29
‑‑ ‑‑ простий 15
мономорфізм 5
напівгрупа 4
найбільший спільний дільник
чисел 8
‑‑ ‑‑ ‑‑ поліномів 12
найменше спільне кратне
поліномів 12
норма 41
носій алгебраїчної структури 4
область цілісності 5
операція бінарна 4
період полінома 35
підгрупа 5
підкільце 6
підполе 17
‑‑ власне 17
таблиця індексів 34
теорема Безу 15
‑‑ Лагранжа 5
‑‑ про автоморфізми
скінченних полів 44
‑‑ -- “башту” розширень 20
‑‑ ‑‑ властивості норми 41
‑‑ ‑‑ властивості сліду 39
‑‑ ‑‑ гомоморфізм кілець 7
‑‑ ‑‑ існування та єдиність
скінченних полів 25
‑‑ ‑‑ канонічний розклад
полінома 13
‑‑ критерій підполя 26
‑‑ про мультиплікативну групу
скінченного поля 27
‑‑ ‑‑ нормальний базис 43
‑‑ ‑‑ степені поліномів 10
‑‑ ‑‑ транзитивність сліду 41
характеристика поля 18
фактор-кільце 6
‑‑ ‑‑ поліномів 13
ядро гомоморфізму 7
|
Date: 2015-09-18; view: 347; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |