
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Двойственные задачи
Каждой ЗЛП можно поставить в соответствие другую задачу, называемую двойственной или сопряжённой. Первоначальная задача называется исходной, а обе ЗЛП образуют пару двойственных (сопряжённых) задач.
Выделяют симметричные (когда исходная ЗЛП является стандартной), несимметричные (когда исходная ЗЛП является канонической), смешанные (когда исходная ЗЛП задана в общем виде) двойственные задачи.
| Исходная ЗЛП | Двойственная ЗЛП |
| Симметричные пары | |
F (Х) = СХ → max,
АХ 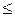 В, В,
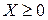
| Z (Y) = YB → min,
АTY 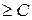 , ,

|
F (Х) = СХ → min,
АХ 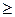 В, В,
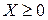
| Z (Y) = YB → max,
АTY 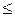 C, C,

|
| Несимметричные пары | |
F (Х) = СХ → max,
АХ = В,
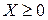
| Z (Y) = YB → min,
АTY 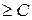
|
F (Х) = СХ → min,
АХ = В,
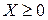
| Z (Y) = YB → max,
АTY 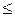 C C
|
Здесь C = 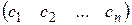 , Y =
, Y = 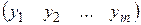 ,
,
A = 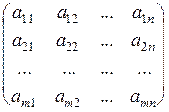 , А T =
, А T = 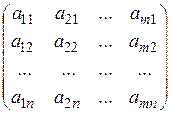 ,
,  ,
, 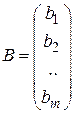 .
.
Замечание. По правилу умножения матриц матрицу А можно умножить на матрицу В, если число k столбцов матрицы А равно числу строк матрицы В. При этом результатом умножения будет матрица С, у которой строк столько же, сколько их в матрице А, и столько же столбцов, сколько их в матрице В:
A m ´ k × B k ´ n = С m ´ n Û " i, j: cij = аi1 b1j + аi2 b2j +... + аik bkj.
Поэтому в записи двойственных ЗЛП матрицы C = 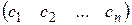 , Y =
, Y = 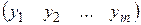 в зависимости от ситуации следует рассматривать как вектор-строку или как вектор-столбец. Так, в записи F (Х) = СХ матрица C является вектор-строкой (1 строка и n столбцов). В записи для системы ограничений АTY
в зависимости от ситуации следует рассматривать как вектор-строку или как вектор-столбец. Так, в записи F (Х) = СХ матрица C является вектор-строкой (1 строка и n столбцов). В записи для системы ограничений АTY 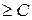 матрица C – вектор-столбец (n строк и 1 столбец), Y - вектор-столбец (m строк и 1 столбец). А в случае Z (Y) = YB матрица Y – уже вектор-строка (1 строка и m столбцов).
матрица C – вектор-столбец (n строк и 1 столбец), Y - вектор-столбец (m строк и 1 столбец). А в случае Z (Y) = YB матрица Y – уже вектор-строка (1 строка и m столбцов).
Двойственные задачи связаны между собой следующим образом:
· в одной задаче ищут максимум целевой функции, в другой - её минимум;
· коэффициенты сj целевой функции исходной задачи являются свободными членами системы ограничений двойственной задачи;
· свободные члены bi системы ограничений исходной задачи служат коэффициентамицелевой функции двойственной задачи;
· матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи.
Алгоритм составления симметричной двойственной задачи
1) Привести все неравенства системы ограничений исходной задачи к виду, когда знаки неравенств направлены в одну сторону: или все 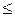 (если ищут максимум целевой функции), или все
(если ищут максимум целевой функции), или все 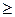 (если ищут минимум целевой функции). Те неравенства, в которых данное требование нарушается, следует умножить на (- 1).
(если ищут минимум целевой функции). Те неравенства, в которых данное требование нарушается, следует умножить на (- 1).
2) Составить целевую функцию, коэффициентами которой являются свободные члены системы ограничений исходной задачи; число неизвестных равно числу неравенств системы ограничений исходной задачи:
Z (Y) = 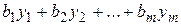 .
.
3) Если в исходной задаче ищут максимум целевой функции, то в двойственной - её минимум, и наоборот.
4) Составить систему ограничений исходя из того, что
· её коэффициенты образуют транспонированную матрицу коэффициентов системы ограничений исходной задачи;
· знаки неравенств меняются на противоположные тем, которые в системе ограничений исходной задачи;
· её свободные члены - коэффициенты сj целевой функции исходной задачи.
5) Записать условие неотрицательности для переменных yj.
Пример 7. Составить двойственную задачу к ЗЛП:
F (Х) = 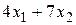 → max,
→ max,
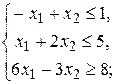
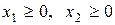 .
.
Решение. Исходная ЗЛП является стандартной (в системе ограничений только неравенства), поэтому воспользуемся алгоритмом составления симметричной двойственной задачи.
1) Приведём все неравенства системы ограничений исходной задачи к виду, когда знаки неравенств направлены в одну сторону: 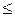 , т.к. ищут максимум целевой функции. Для этого последнее неравенство умножим на (- 1). Получим систему ограничений исходной задачи в виде
, т.к. ищут максимум целевой функции. Для этого последнее неравенство умножим на (- 1). Получим систему ограничений исходной задачи в виде
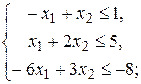
2) Составим целевую функцию двойственной задачи. Система ограничений исходной задачи содержит 3 неравенства, следовательно, число неизвестных целевой функции также равно 3. Обозначим неизвестные: 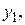
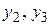 . Коэффициентами целевой функции будут свободные члены системы ограничений исходной задачи, т.е. числа 1, 5, -8. Так как в исходной задаче требуется найти максимум целевой функции, то в двойственной нужно найти её минимум. Таким образом, имеем
. Коэффициентами целевой функции будут свободные члены системы ограничений исходной задачи, т.е. числа 1, 5, -8. Так как в исходной задаче требуется найти максимум целевой функции, то в двойственной нужно найти её минимум. Таким образом, имеем
Z (Y) =  → min.
→ min.
3) Составим систему ограничений
A = 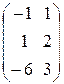 , А T =
, А T = 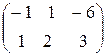
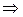
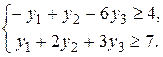
4) Условие неотрицательности для переменных yj:
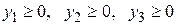 .
.
Двойственная задача получена. Запишем симметричную пару двойственных задач:
| Исходная ЗЛП | Двойственная ЗЛП |
F (Х) = 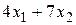 → max, → max,
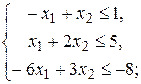
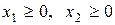
| Z (Y) =  → min, → min,
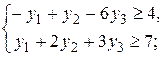
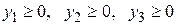
|
Алгоритм составления несимметричной двойственной задачи
1) Составить целевую функцию, коэффициентами которой являются свободные члены системы ограничений исходной задачи; число неизвестных равно числу уравнений системы ограничений исходной задачи:
Z (Y) = 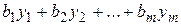 .
.
2) Если в исходной задаче ищут максимум целевой функции, то в двойственной - её минимум, и наоборот.
3) Составить систему ограничений исходя из того, что
· её коэффициенты образуют транспонированную матрицу коэффициентов системы ограничений исходной задачи;
· знаки неравенств проставляются в зависимости от того, максимум или минимум ищут в исходной задаче: если исходная ЗЛП – на максимум, то в неравенствах знаки 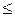 , если исходная ЗЛП – на минимум, то знаки
, если исходная ЗЛП – на минимум, то знаки 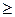 ;
;
· её свободные члены - коэффициенты сj целевой функции исходной задачи.
Переменные yj могут быть произвольными по знаку.
Пример 8. Составить двойственную задачу к ЗЛП:
F (Х) =  → min,
→ min,
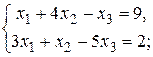
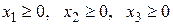 .
.
Решение. Исходная ЗЛП является канонической (в системе ограничений только уравнения), поэтому воспользуемся алгоритмом составления несимметричной двойственной задачи.
1) Составим целевую функцию двойственной задачи. Система ограничений исходной задачи содержит 2 уравнения, следовательно, число неизвестных целевой функции также равно 2. Обозначим неизвестные: 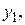
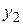 . Коэффициентами целевой функции будут свободные члены системы ограничений исходной задачи, т.е. числа 9, 2.
. Коэффициентами целевой функции будут свободные члены системы ограничений исходной задачи, т.е. числа 9, 2.
Так как в исходной задаче требуется найти минимум целевой функции, то в двойственной нужно найти её максимум. Таким образом, имеем
Z (Y) = 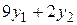 → max.
→ max.
2) Составим систему ограничений двойственной задачи. Её коэффициенты образуют транспонированную матрицу A T коэффициентов системы ограничений исходной задачи. Составим матрицы А, A T:
А = 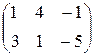 , A T =
, A T = 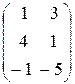 .
.
Знаки неравенств системы ограничений двойственной задачи будут 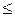 , т.к. исходная ЗЛП – на максимум. Свободные члены системы ограничений двойственной задачи - коэффициенты целевой функции исходной задачи, т.е. числа 1, - 6, - 1.
, т.к. исходная ЗЛП – на максимум. Свободные члены системы ограничений двойственной задачи - коэффициенты целевой функции исходной задачи, т.е. числа 1, - 6, - 1.
Система ограничений двойственной задачи имеет вид:
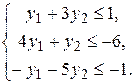
Переменные 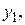
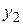 могут быть произвольными по знаку.
могут быть произвольными по знаку.
Получили следующую несимметричную пару двойственных задач:
| Исходная ЗЛП | Двойственная ЗЛП |
F (Х) =  → min, → min,
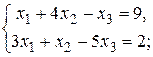
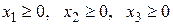
| Z (Y) = 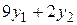 → max, → max,
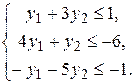
|
Date: 2015-09-20; view: 613; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |