Опорное решение ЗЛП

Рассмотрим систему уравнений (1):

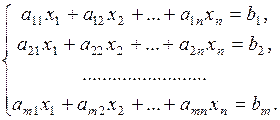
Из курса алгебры известно, что с помощью элементарных преобразований (умножение любого уравнения системы на ненулевое число; прибавление к одному уравнению другого, умноженного на любое число; перестановка местами уравнений системы) можно привести эту систему к стандартному виду. Для этого в каждом уравнении оставляют переменную, которую исключают из всех остальных уравнений системы. Такую переменную называют базисной.

Коэффициент при базисной переменной равен единице, причём в каждом уравнении базисной можно сделать любую переменную.

Переменные, не являющиеся базисными, называют свободными.

Если в совместной (имеющей решения) системе число уравнений меньше числа неизвестных, то решений у такой системы будет бесконечно много. В этом случае свободным переменным можно придать любые значения, а базисные переменные выразить через значения свободных переменных.

Систему уравнений, приведённую к виду, когда в каждом уравнении есть своя базисная переменная, называют записанной в стандартном виде.

Пусть базисной переменной 1-го уравнения является переменная х ₁, 2-го уравнения - переменная х ₂, …, m -го уравнения - переменная х_m. Коэффициенты в i -ом уравнении при неизвестных х_j обозначим через d_ij; свободные коэффициенты - b_{i 0}, тогда получим систему, приведённую к стандартному виду:

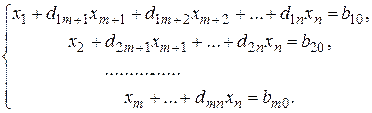(2)

Общее решение системы (2):

(3)

Переменные х_{m+ 1}, х _{m+ 2}, …, х_n являются свободными переменными, они могут принимать любое значение.

Пусть система (1) и эквивалентная ей система (2) являются системами ограничений некоторой канонической ЗЛП. Поэтому на переменные х ₁, х ₂, …, х_n (как свободные, так и базисные) наложены ограничения неотрицательности.

Среди бесконечного множества решений системы (1) выделим конечный набор решений, каждое из которых является опорным.

Опр.: Решение Х = (х ₁, х ₂, …, х_m, 0, 0, …, 0), в котором все свободные переменные равны нулю, а х ₁, х ₂, …, х_m неотрицательны, называется опорным решением (ОР).

Из определения ОР и системы (3) следует, что значения базисных переменных равны правым частям (свободным членам) системы (2).

Для того, чтобы все базисные переменные были неотрицательными, все правые части системы (2) должны быть неотрицательными.

Для одной системы можно найти множество ОР. В общем случае можно выбрать 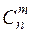наборов базисных переменных, следовательно, число ОР может быть не более .

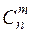Пример 2. Найти ОР системы уравнений

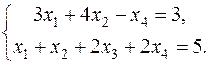
Решение. Для данной системы может быть 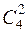= 6 вариантов выбора базисных переменных: (х ₁, х ₂), (х ₁, х ₃), (х ₁, х ₄), (х ₂, х ₃), (х ₂, х ₄), (х ₃, х ₄).

1) Пусть х ₄ будет базисной переменной. Умножим первое уравнение на (- 1), чтобы получить коэффициент при х ₄ равный 1. Исключим х ₄ из 2-го уравнения. Для этого прибавим ко второму уравнению первое, умноженное на 2. Получим эквивалентную систему

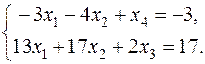
Примем во 2-м уравнении за базисную переменную х ₃. Выразим базисные переменные х ₃, х ₄ через свободные х ₁, х ₂:

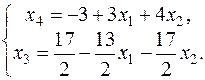
Таким образом, система имеет бесконечное множество решений

,

где х ₁, х ₂ - любые действительные числа.

Если х ₂ = х ₁ = 0, поручим решение (0, 0, 17/2, -3), которое не является ОР, т.к. х ₄ < 0.

2) Пусть х ₁ будет базисной переменной. Умножим первое уравнение на (1/3), чтобы получить коэффициент при х ₁ равный 1. Исключим х ₁ из 2- го уравнения. Для этого прибавим ко второму уравнению первое, умноженное на (- 1). Получим эквивалентную систему

Примем во 2-м уравнении за базисную переменную х ₃, разделим его на 2. Выразим базисные переменные х ₁, х ₃ через свободные х ₂, х ₄:

При х ₄ = х ₂ = 0 имеем опорное решение Х = (1, 0, 2, 0).

Опр.: ОР называется вырожденным, если все базисные переменные больше нуля, и невырожденным, если есть хотя бы одна равная нулю базисная переменная.

Опр.: Векторы-столбцы коэффициентов при неизвестных в системе ограничений ЗЛП называются векторами условий.

Опр.: Базисом ОР называется базис системы векторов условий ЗЛП, в состав которого входят векторы, соответствующие отличным от нуля координатам ОР.