Система материальных точек. Твёрдое тело

Системой материальных точек (или механической системой) называют такую совокупность точек, в которой положение или движение каждой точки зависит от положения и движения всех остальных.

Систему материальных точек, движение которых не ограничено никакими связями, а определяется лишь действующими на эти точки силами, называют системой свободных точек. Примером системы свободных точек может служить Солнечная система, планеты которой рассматривают в астрономии как материальные точки. Планеты свободно перемещаются по орбитам, зависящим от действующих на них сил.

Система материальных точек, движения которых ограничиваются наложенными на точки связями, называется системой несвободных точек. Примером системы несвободных точек может служить любой механизм или машина, у которых движения отдельных элементов ограничены связями.

Материальное тело мы также будем рассматривать как систему материальных частиц (точек), образующих это тело.

Механическая система с неголономными связями называется неголономной системой.

Механическая система с голономными связями называется голономной системой.

Известно, что механическое действие связей на точки системы выражается силами, называемыми реакциями связей. Таким образом, все силы, действующие на систему несвободных точек, можно разделить на задаваемые (активные) силы и реакции связей.

Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы. Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом 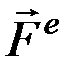, а внутренние – 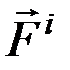(индексы 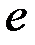и 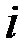происходят от начальных букв французских слов: exterieur – внешний и interieur – внутренний).

Как внешние, так и внутренние силы могут быть, в свою очередь, или активными, или реакциями связей. Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем.

Таким образом, любая сила, действующая на точку механической системы в соответствии с приведёнными двумя классификациями сил, является внешней пли внутренней. В то же время она является задаваемой силой или реакцией связи. Движение точек механической системы зависит как от внешних, так и от внутренних сил.

Внутренние силы обладают следующими свойствами.

1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. По третьему закону динамики, любые две точки системы (рис. 15) действуют друг на друга с равными по модулю и противоположно направленными силами и 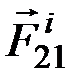,сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то

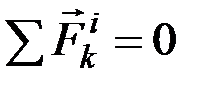. (5.1)

2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю.

Рис. 15

Действительно, если взять произвольный центр ,то из рис. 15 видно, что

.

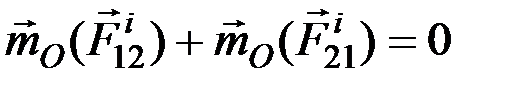Аналогичный результат получится при вычислении моментов относительно оси. Следовательно, и для всей системы будет выполняться условие:

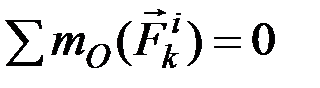или 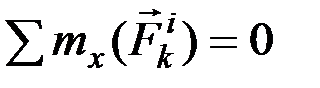. (5.2)

Из доказанных свойств не следует, что внутренние силы взаимно уравновешиваются и не влияют на движение системы, так как эти силы приложены к разным материальным точкам или телам и могут вызвать взаимные перемещения этих точек или тел. Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно твёрдое тело.

Центр масс. Движение системы, кроме действующих сил, зависит от ее суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образующих систему:

.

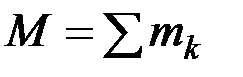В однородном поле тяжести, для которого g = const, вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести (см. Алексеев В. В. Теоретическая механика. Статика. – Новосибирск, 2008), к виду, явно содержащему массу. Для этого положим 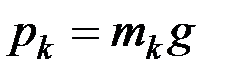, , 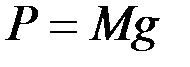после чего, сократив на 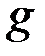,получим:

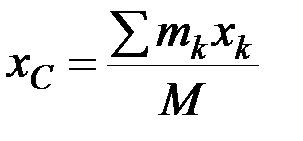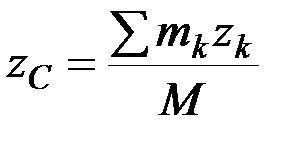, , . (5.3)

В полученные равенства входят только массы 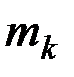материальных точек (частиц), образующих тело, и координаты 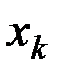, , 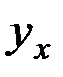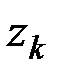этих точек. Следовательно, положение точки действительно характеризует распределение масс в теле или в любой механической системе, если под , , 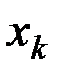, понимать соответственно массы и координаты точек этой системы.

Геометрическая точка 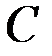, координаты которой определяются формулами (5.3), называется центром масс или центром инерции механической системы.

Если положение центра масс определять его радиус-вектором 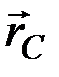,то для его определения используется формула:

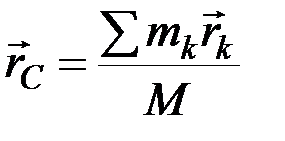, (5.4)

где – радиусы-векторы точек, образующих систему.

Хотя положение центра масс совпадает с положением центра тяжести тела, находящегося в однородном поле тяжести, понятия эти не являются тождественными. Понятие о центре тяжести как о точке, через которую проходит линия действия равнодействующей сил тяжести, по существу имеет смысл только для твёрдого тела, находящегося в однородном поле тяжести. Понятие же о центре масс как о характеристике распределения масс в системе имеет смысл для любой системы материальных точек или тел, причем это понятие сохраняет свой смысл независимо от того, находится ли данная система под действием каких-нибудь сил или нет.

Date: 2015-09-03; view: 1998; Нарушение авторских прав