Способы задания топологии

Задать топологическое пространство – значит задать носитель Х и топологию 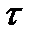, то есть указать те подмножества Х, которые будем считать открытыми.

Примеры 1. Произвольное множество X можно сделать топологическим пространством, если называть открытыми все его подмножества, то есть на любом X включим в топологию вообще все подмножества X (в том числе и все его точки, то есть одноточечные подмножества), само X и пустое подмножество. Такая топология называется дискретной: 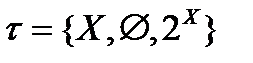, где 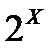- все подмножества множества Х.

2. Второй крайний случай – антидискретная (тривиальная) топология или топология слипшихся точек: на любом носителе X рассмотрим топологию, в которой всего два множества: все X и пустое: .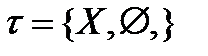

3. Вещественная прямая R является топологическим пространством, если назвать открытыми множествами произвольные (пустые, конечные или бесконечные) объединения конечных или бесконечных интервалов.

Действительно, вся числовая прямая очевидным образом открыта, пустое множество включают в число открытых по определению (это непротиворечиво, поскольку в пустом множестве нет точек, тогда можно считать, что каждая из них (!) входит в пустое множество с некоторой 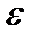-окрестностью). Топологию, состоящую из обычных открытых множеств на числовой прямой, называют нормальной (обычной) топологией. Точно также строится нормальная топология в 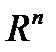. Таким образом,нормальная топология 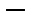это топология стандартных метрических пространств.

4 . Топология Зарисского на числовой прямой. В эту топологию включены вся прямая, пустое множество, и все множества на прямой, дополнения которых до R состоят из конечного числа точек. То есть открытые интервалы получены выбрасыванием из прямой конечного числа точек.

5 . Правая стрелка 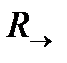. Эта топология на числовой прямой состоит из всей прямой, пустого множества, и всех открытых интервалов вида 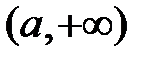, где a - точка прямой. Аналогично можно задать и левую стрелку.

6. 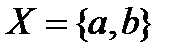- топологическое двоеточие. Дискретная топология: 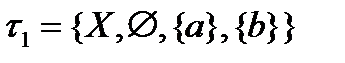,антидискретная топология: 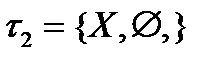. На двоеточии возможны ещё две топологи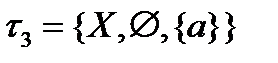и: и 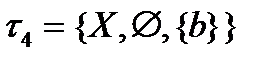. Метризуема (то есть можно ввести расстояние) только дискретная топология: 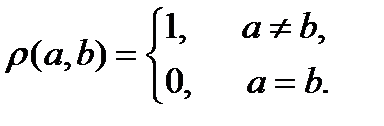Остальные – нет. В случае, например, 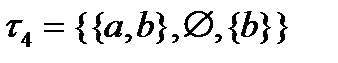открыты 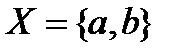, пустое множество 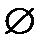и 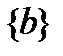, замкнуты 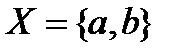пустое множество 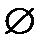и .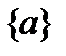

База

Комментарий. Тривиальную и дискретную топологию можно задать, описав все входящие в них множества. С обычной топологией это невозможно, и пришлось описывать ее с помощью свойства, которому удовлетворяют ее множества. Чтобы избежать этого неудобства, было введено понятие базы топологии.

Определение 1. Набор открытых множеств 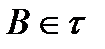называется базой топологии 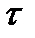, если любое множество из 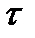есть (возможно, бесконечное) объединение множеств из В. Всякая база 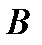в топологическом пространстве Т=(Х, 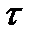). обладает следующими двумя свойствами:

1) любая точка 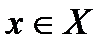содержится хотя бы в одном ;

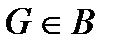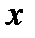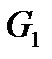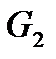2) если точка содержится в пересечении двух множеств и из 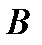, то существует такое 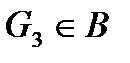, что .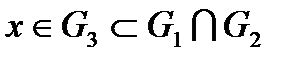

Пример. Базой обычной топологии на прямой являются 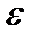-окрестности. Действительно, обычное открытое множество характеризуется тем, что каждая его точка имеет некоторую 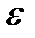-окрестность, входящую в это множество. Очевидно, что само множество есть объединение указанных 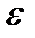-окрестностей всех его точек. Всякое метрическое пространство является топологическим пространством, базу топологии которого составляют открытые шары этого пространства.

Определение 2. Говорят, что топологическое пространство имеет счётную базу, если топология этого пространства имеет базу, состоящую из счетного набора множеств (то есть множества, входящие в эту базу, можно занумеровать натуральными числами).

Пример. Обычная топология на прямой имеет счетную базу - это 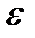-окрестности с рациональным 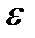, центрами которых являются рациональные точки (множество рациональных чисел счетно). Дискретная топология на прямой не имеет счетной базы: в любую базу этой топологии должны входить все точки прямой, а это множество имеет мощность континуума.

Date: 2015-09-03; view: 2306; Нарушение авторских прав