Метод Остроградского

Пусть знаменатель несократимой дроби 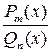имеет вид

.

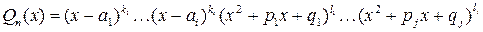Метод Остроградского заключается в использовании формулы

.

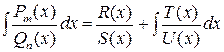В ней многочлены 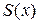и 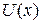имеют вид

,

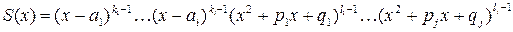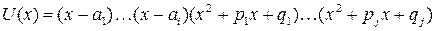
соответственно и могут быть вычислены без разложения многочлена 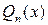на произведение неприводимых множителей.

Действительно, 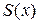является наибольшим общим делителем двух многочленов 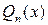и , и может быть вычислен при помощи алгоритма Евклида, который излагается в курсе алгебры.

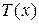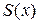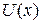Остается вычислить многочлены и как многочлены с неопределенными коэффициентами степени на единицу ниже, чем и соответственно. Для вычисления указанных неопределенных коэффициентов следует продифференцировать формулу Остроградского, привести результат дифференцирования к общему знаменателю и сопоставить коэффициенты при одинаковых степенях х в числителях.

Метод Остроградского особенно эффективен, когда корни 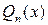в основном являются кратными или когда вызывает затруднение нахождение корня .

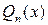Вычислим .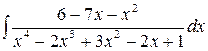

Имеем , .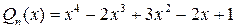

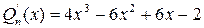Наибольший общий делитель этих многочленов равен

.

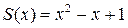Поделив 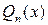на 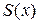«столбиком», найдем

.

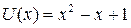и 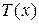задаем как многочлены первой степени с неопределенными коэффициентами, и формула Остроградского принимает вид

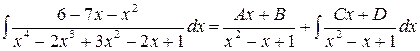
Продифференцируем эту формулу:

.

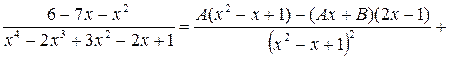
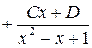Результат дифференцирования приводим к общему знаменателю, после чего сопоставляем числители. Получим

.

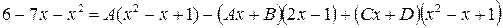Сопоставляя коэффициенты пр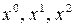и и 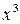, получим систему уравнений:

Решая эту систему, найдем 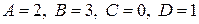. Таким образом формула Остроградского принимает вид:

.

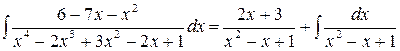Вычислим интеграл в правой части:

.

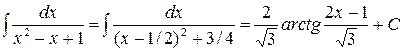Окончательно имеем

.

Рассмотрим еще один пример.

Разложим знаменатель на множители:

.

Отсюда .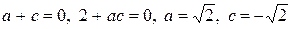

.

Приравнивая коэффициенты:

.

.

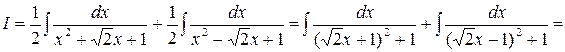
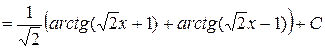Упражнение. Применяя метод Остроградского найти соответствующие интегралы из расчетно-графической работы.

Date: 2015-09-02; view: 590; Нарушение авторских прав