
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница
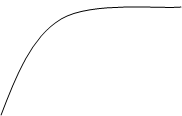 1. Криволинейной трапецией называется фигура, ограниченная линией у = f (x) и прямыми х=а, х=b, у= 0. Будем считать, что f (x)
1. Криволинейной трапецией называется фигура, ограниченная линией у = f (x) и прямыми х=а, х=b, у= 0. Будем считать, что f (x) 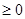 на [ a; b ].
на [ a; b ].





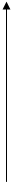 у у = f (x)
у у = f (x)

0 а х 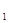 х
х 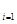
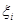 х
х 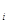 b x
b x
Разобьём отрезок [ a; b ] произвольным образом на п частей точками а=х  < x
< x 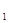 <…< х
<…< х 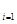 < х
< х 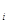 <…< х
<…< х 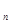 =b.
=b.
На каждом отрезке [ х 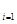 ; х
; х 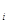 ] возьмём произвольную точку
] возьмём произвольную точку 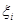 ивычислимзначение f (
ивычислимзначение f (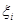 ). Тогда площадь S
). Тогда площадь S 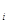 заштрихованного прямоугольника, будет равна
заштрихованного прямоугольника, будет равна
S 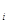 = f (
= f (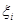 )
) 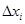 , где
, где 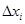 = х
= х 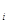 - х
- х 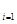 .
.
Площадь S всей трапеции приблизительно равна
S 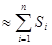
 .
.
Пусть 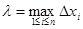 . Естественно считать, что
. Естественно считать, что
S 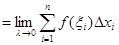 . (6.2)
. (6.2)
К пределам вида (6.2) приводят много других задач, поэтому возникает необходимость всестороннего изучения таких пределов независимо от конкретного содержания той или иной задачи.
Пусть функция у = f (x) определена на отрезке [ a; b ]. Разобьём этот отрезок на п произвольных частей точками
а=х  < x
< x 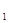 <…< х
<…< х 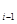 < х
< х 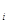 <…< х
<…< х 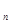 =b.
=b.
На каждом из созданных отрезков [ х 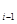 ; х
; х 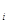 ] возьмём произвольную точку
] возьмём произвольную точку 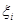 и составим сумму
и составим сумму
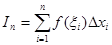 , где
, где 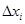 = х
= х 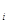 - х
- х 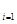 ,
,
которую будем называть интегральной суммой функции f (x).
Обозначим 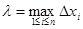 . Если существует конечный предел интегральной суммы
. Если существует конечный предел интегральной суммы 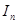 , при
, при 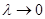 , который не зависит ни от способа разбиения отрезка [ a; b ], ни от выбора точек
, который не зависит ни от способа разбиения отрезка [ a; b ], ни от выбора точек 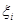 , то этот предел называется определённым интегралом функции f (x) на отрезке [a;b] и обозначается символом
, то этот предел называется определённым интегралом функции f (x) на отрезке [a;b] и обозначается символом  , где функция f (x) называется интегрированной на отрезке [a;b].
, где функция f (x) называется интегрированной на отрезке [a;b].
То есть, по определению,
 =
= 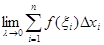 .
.
Числа а и b называются соответственно нижним и верхним пределом интегрирования.
Относительно существования определённого интеграла имеет место такая теорема
Теорема 6.3. Если функция f (x) ограничена на отрезке [a;b] и непрерывна на нём везде, кроме конечного числа точек, то она интегрируема на этом отрезке.
2. Если f (x) 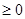 , то
, то  равен площади соответствующей криволинейной трапеции:
равен площади соответствующей криволинейной трапеции:  = S. Если f (x)<0, то
= S. Если f (x)<0, то  = - S.
= - S.
Отсюда следует, что если на симметричном относительно начала координат отрезке [-a;а], а>0 задана нечётная функция, то 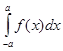 =0. Например,
=0. Например, 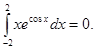 Если функция f (x) чётная, то
Если функция f (x) чётная, то 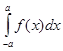 =2
=2 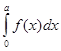 .
.
Свойства определённого интеграла
Будем считать, что все интегралы, которые рассматриваются, существуют.
1.  =
= 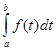 . Величина определённого интеграла не зависит от обозначения переменной интегрирования.
. Величина определённого интеграла не зависит от обозначения переменной интегрирования.
2. 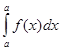 =0.
=0.
3.  = -
= - 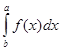 .
.
4.  =
= 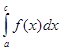 +
+ 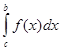 .
.
5. 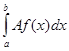 = А
= А  .
.
6. 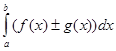 =
= 
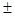
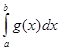 .
.
7. Если на отрезке [a;b] f (x) 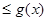 , то
, то 
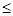
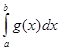 .
.
8. Если т и М – соответственно наименьшее и наибольшее значения функции f (x), на отрезке [a;b], то
т (b-a) 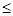

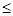 M (a-b).
M (a-b).
9. (теорема о среднем значении функции).
Если функция f (x) непрерывна на отрезке [a;b], то на этом отрезке существует такая точка с, что  = f (с) (b-a).
= f (с) (b-a).
Число f (с)= 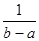
 называют средним значением функции f (x) на отрезке [a;b].
называют средним значением функции f (x) на отрезке [a;b].
3. Пусть функция у = f (x) непрерывна на отрезке [ a; b ]. Тогда она интегрируема на любом отрезке [ a; х ] 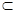 [ a; b ], то есть для произвольного х
[ a; b ], то есть для произвольного х 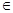 [ a; b ] существует интеграл
[ a; b ] существует интеграл 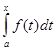 , который, очевидно, является функцией от х. Обозначим эту функцию через Ф(х)
, который, очевидно, является функцией от х. Обозначим эту функцию через Ф(х)
Ф(х)= 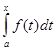 (6.3)
(6.3)
и назовём интегралом с переменным верхним пределом.
Теорема 6.4. Если функция f (x) непрерывна на отрезке [a;b], то интеграл (6.3) является дифференцированной функцией на этом отрезке, причём Ф’(х)= f (x).
Другими словами, интеграл с переменным верхним пределом является одной из первообразных подынтегральной функции f (x).
Пусть функция у = f (x) непрерывна на отрезке [ a; b ] и F (x) – первообразная функции f (x). Поскольку функция Ф(х) = 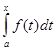 также является первообразной функции f (x), а две первообразные одной функции отличаются только постоянным слагаемым, то
также является первообразной функции f (x), а две первообразные одной функции отличаются только постоянным слагаемым, то
Ф(х)= F (x) + С, или 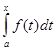 = F (x)+ С. (6.4)
= F (x)+ С. (6.4)
Считая в (6.4) х=а, получим
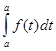 =0= F (а)+ С
=0= F (а)+ С  С=- F (а).
С=- F (а).
Равенство (6.4) можно записать в виде
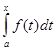 = F (x) - F (а).
= F (x) - F (а).
Заменим х на b и t на x. Получим формулу
 = F (b) - F (а),
= F (b) - F (а),
которая называется формулой Ньютона-Лейбница. Часто её записывают в виде
 = F (x)
= F (x) 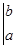 .
.
Формула Ньютона-Лейбница даёт удобный способ вычисления определённых интегралов.
Если функция и=и (х), v=v (x) и их производные и’ (х), v’ (x) непрерывны на отрезке [ a; b ], то справедлива формула интегрирования по частям
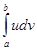 = uv
= uv 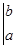 -
- 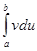 .
.
Если функция f (x) непрерывна на отрезке [a;b], а функция х= 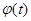 и её производная х’=
и её производная х’= 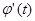 непрерывны на отрезке [ a; b ], причём
непрерывны на отрезке [ a; b ], причём 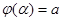 ,
, 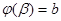 , то справедлива формула
, то справедлива формула
 =
= 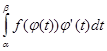 .
.
Заметим, что, в отличие от неопределённого интеграла, в определённом интеграле нет необходимости делать обратную замену, поскольку появляются новые пределы интегрирования.
При определении определённого интеграла

как предела интегральных сумм предусматривалось, что: 1) отрезок интегрирования [a;b] конечный и 2) подынтегральная функция f (x) на этом отрезке ограничена. Такой интеграл называется собственным, хотя слово «собственнный», как правило, опускается.
Если же хотя бы одно из двух приведенных условий нарушается, то интеграл называют несобственным. Различают два вида несобственных интеграла.
1. Несобственные интегралы с бесконечными пределами интегрирования
(несобственные интегралы І рода).
Если функция f (x) непрерывна при 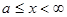 , то считают
, то считают
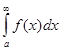 =
= 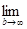
 (6.5)
(6.5)
и в зависимости от существования или не существования конечного предела в правой части формулы (6.5) несобственный интеграл І рода 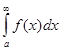 называют сходящимся или расходящимся. Аналогично
называют сходящимся или расходящимся. Аналогично
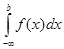 =
= 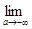
 ,
,  =
= 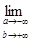
 .
.
2. Несобственные интегралы от неограниченных функций (несобственные интегралы ІІ рода).
Если функция f (x) неограничена в любой окрестности точки с 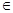 (a;b) и непрерывна при
(a;b) и непрерывна при 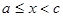 , и
, и 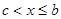 , то по определению считают
, то по определению считают
 =
= 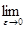
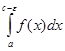 +
+ 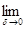
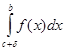 . (6.6)
. (6.6)
Если оба предела в правой части равенства (6.6) существуют и конечны, то несобственный интеграл считают сходящимся, в противном случае – расходящимся.
Если функция f (x) неограничена только на одном из концов отрезка [ a; b ], то соответствующие определения несобственного интеграла ІІ рода упрощаются:
 =
= 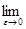
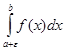 ,
,
если функция f (x) неограничена в точке х=а, и
 =
= 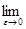
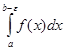 ,
,
если функция f (x) неограничена в точке х=b.
Лекция 15. Тема – Дифференциальные уравнения. Дифференциальные уравнения с разделяющимися переменными, однородные дифференциальные уравнения.
План.
Основные понятия.
Date: 2015-07-27; view: 408; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |