
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Локальные экстремумы функции высших порядков
1. Пусть функция z=f (x; у) непрерывна в некоторой окрестности точки М (x; у) вместе со своими частными производными 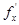 (х; у),
(х; у), 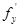 (х; у). Выберем приращение
(х; у). Выберем приращение 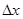 и
и 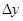 так, чтобы точка (х+
так, чтобы точка (х+ 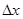 ;у+
;у+ 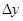 ) принадлежала рассматриваемой окрестности.
) принадлежала рассматриваемой окрестности.
Если полное приращение функции z=f (x; у) в точке М (x; у)
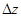 = f (x+
= f (x+ 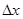 ; у +
; у + 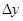 )- f (x; у)
)- f (x; у)
можно записать в виде
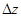 =
= 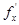 (х; у)
(х; у) 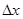 +
+ 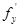 (х; у)
(х; у) 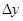 +
+ 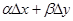 ,
,
где 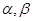 - бесконечно малые функции при
- бесконечно малые функции при 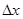
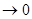 ,
, 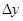
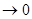 , то функция z=f (x; у) называется дифференцированной в точке М (x; у), а линейная относительно
, то функция z=f (x; у) называется дифференцированной в точке М (x; у), а линейная относительно 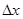 и
и 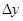 часть её полного приращения
часть её полного приращения 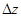 называется полным дифференциалом функции и обозначается
называется полным дифференциалом функции и обозначается
dz= 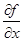
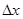 +
+ 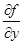
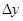 .
.
Дифференциалами независимых переменных называют приращения этих переменных dх= 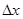 , dу=
, dу= 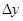 . Поэтому
. Поэтому
dz= 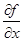 dх +
dх + 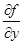 dу,
dу,
или в других обозначениях
dz= 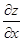 dх +
dх + 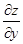 dу.
dу.
Для функции трёх переменных и= f (x; у; z)
dи= 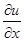 dх +
dх + 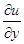 dу+
dу+  dz.
dz.
Полный дифференциал функции z=f (x; у)
dz= 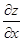 dх +
dх + 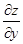 dу,
dу,
который ещё называют дифференциалом первого порядка, зависит от независимых переменных х, у и от их дифференциалов dх, dу. Заметим, что дифференциалы dх, dу не зависят от х, у.
Дифференциалы второго порядка определяют по формуле
d2 z= d (dz).
Тогда
d2 z= d (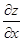 dх+
dх+ 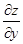 dу)=
dу)= 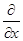 (
(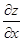 dх+
dх+ 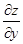 dу) dх+
dу) dх+ 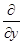 (
(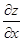 dх+
dх+ 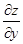 dу) dу=
dу) dу= 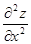 dх2+
dх2+ 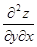 dу dх+
dу dх+
+ 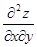 dх dу+
dх dу+ 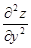 dу2,
dу2,
откуда
d2 z= 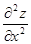 dх2+ 2
dх2+ 2 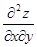 dх dу+
dх dу+ 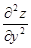 dу2.
dу2.
Символически это можно записать так:
d2 z= (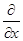 dх+
dх+ 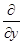 dу)2 z.
dу)2 z.
Аналогично можно получить формулу для полного дифференциала п -го порядка:
dп z= d (dп-1 z) =(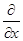 dх+
dх+ 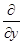 dу) п z.
dу) п z.
2. Производная функции z=f (x; у) в направлении вектора 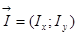 вычисляется по формуле
вычисляется по формуле
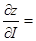
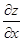
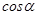 +
+ 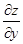
 ,
,
где 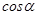 ,
,  - направляющие косинусы вектора
- направляющие косинусы вектора 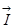 :
:
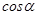 =
= 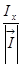 ,
,  =
= 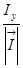 .
.
Если частные производные характеризуют скорость изменения функции в направлении соответствующих координатных осей, то производная в направлении вектора 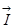 определяет скорость изменения функции в направлении вектора
определяет скорость изменения функции в направлении вектора 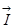 .
.
Градиентом функции z=f (x; у) называется вектор
grad z= (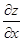 ,
, 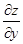 ).
).
Свойства градиента
1. Производная 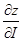 имеет наибольшее значение, если направление вектора
имеет наибольшее значение, если направление вектора 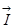 совпадает с направлением градиента, причём это наибольшее значение производной равно
совпадает с направлением градиента, причём это наибольшее значение производной равно 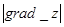 .
.
2. Производная в направлении вектора, перпендикулярного градиенту, равна нулю.
3. Пусть функция z=f (x; у) определена на множестве D и точка М  (х
(х  ; у
; у  )
) 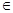 D. Если существует окрестность точки М
D. Если существует окрестность точки М  , которая принадлежит множеству D, и для всех отличных от М
, которая принадлежит множеству D, и для всех отличных от М  точек М выполняется неравенство
точек М выполняется неравенство
f (М)< f (М0) (f (М)> f (М0)),
то точку М  называют точкой локального максимума (минимума) функции z=f (x; у), а число f (М0) - локальным максимумом (минимумом) этой функции. Точки максимума и минимума функции называют её точками экстремума.
называют точкой локального максимума (минимума) функции z=f (x; у), а число f (М0) - локальным максимумом (минимумом) этой функции. Точки максимума и минимума функции называют её точками экстремума.
Теорема 5.1 (необходимые условия экстремума). Если функция z=f (x; у) в точке М  (х
(х  ; у
; у  ) имеет локальный экстремум, то в этой точке частные производные
) имеет локальный экстремум, то в этой точке частные производные 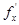 ,
, 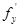 равны нулю или не существуют.
равны нулю или не существуют.
Точки, в которых 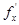 =
= 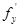 = 0, называются стационарными. Стационарные точки и точки, в которых частные производные не существуют, называются критическими.
= 0, называются стационарными. Стационарные точки и точки, в которых частные производные не существуют, называются критическими.
Поэтому функция может достигать экстремальных значений только в критических точках; однако не всякая критическая точка является точкой экстремума.
Пусть в стационарной точке М  (х
(х  ; у
; у  ) и некоторой её окрестности функция z=f (x; у) имеет непрерывные частные производные второго порядка. Введём обозначения:
) и некоторой её окрестности функция z=f (x; у) имеет непрерывные частные производные второго порядка. Введём обозначения:
А= 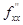 (х
(х  ; у
; у  ), В=
), В= 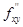 (х
(х  ; у
; у  ), С=
), С= 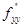 (х
(х  ; у
; у  ),
), 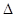 = АС-В2.
= АС-В2.
Теорема 5.2 (достаточные условия экстремума).
1. Если 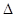 >0, то функция z=f (x; у) в точке М
>0, то функция z=f (x; у) в точке М  имеет экстремум, причём максимум при А <0 и минимум при А >0.
имеет экстремум, причём максимум при А <0 и минимум при А >0.
2. Если 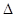 <0, то в точке М
<0, то в точке М  нет экстремума.
нет экстремума.
Для случая, когда количество переменных п >2, пользуются такой теоремой.
Теорема 5.3 Функция и = f (х 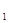 ;...; х
;...; х 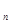 ) имеет минимум в стационарной точке М
) имеет минимум в стационарной точке М  , если дифференциал второго порядка этой функции в точке М
, если дифференциал второго порядка этой функции в точке М  положителен d2f (М
положителен d2f (М  )>0, и максимум, если d2f (М
)>0, и максимум, если d2f (М  )<0.
)<0.
Пример. Исследовать на экстремум функцию
z= (х+ 2)2+(у -1)2.
Решение.
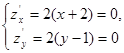

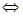
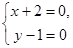
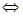
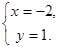
Функция имеет одну критическую точку М (-2;1).
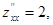
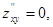
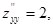 А= 2, В= 0, С= 2,
А= 2, В= 0, С= 2,
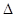 = АС-В2 = 2*2-02= 4>0, А >0.
= АС-В2 = 2*2-02= 4>0, А >0.
Значит, в точке М (-2;1) функция имеет минимум: min z=z (-2;1)=(-2+2)2+(1-1)2=0.
Лекция 12. Тема – Интегральное исчисление функций. Первообразная. Неопределённный интеграл. Методы интегрирования.
План.
1. Первообразная функции. Неопределённный интеграл. Свойства неопределённого интеграла.
Таблица основных интегралов. Метод подстановки (замены переменной).
3. Интегрирование по частям. Интегралы, которые ”не берутся”.
Интеграл – одно из центральных понятий математики. Оно возникло в связи с двумя задачами: 1) о восстановлении функции по её производной; 2) о вычислении площади криволинейной трапеции. Эти задачи приводят к двум связанным между собой видам интегралов: определённого и неопределённого. Термин ”интеграл” ввёл Якоб Бернулли в 1690 году.
1. Функция F (x) называется первообразной функции f (x) на некотором промежутке, если во всех точках этого промежутка выполняется равенство F’ (x)= f (x).
Например. первообразными функции f (x)=3 х 2 будут функции х 3, х 3+1, х 3+0,5 и вообще F (x)= х 3+ С, где С – произвольная постоянная, поскольку F’ (x)=(х 3+ С)’=3 х 2. Этот пример показывает, что если функция f (x) имеет одну первообразную, то она имеет их бесконечно много. Возникает вопрос: как найти все первообразные данной функции, если известна одна из них? Ответ даёт такая теорема.
Теорема 6.1 Если F (x) – первообразная функции f (x) на некотором промежутке, то всякая другая первообразная функции f (x) на этом промежутке имеет вид F (x) + С, где С – произвольная постоянная.
Множество всех первообразных F (x) + С функции f (x) называют неопределённым интегралом функции f (x) и обозначают 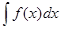 . Таким образом, по определению
. Таким образом, по определению
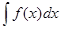 = F (x) + С, если F’ (x)= f (x).
= F (x) + С, если F’ (x)= f (x).
При этом f (x) называют подынтегральной функцией, f (x) dх – подынтегральным выражением, х – переменной интегрирования, знак 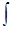 - знаком интеграла, С – постоянной интегрирования.
- знаком интеграла, С – постоянной интегрирования.
Операцию нахождения первообразной функции f (x) называют интегрированием этой функции.
Операции дифференцирования и интегрирования являются обратными по отношению друг к другу.
Возникает вопрос: для каждой ли функции f (x) существует первообразная, а значит, и неопределённый интеграл? Оказывается не для каждой. Но справедлива такая
Теорема 6.2. Всякая непрерывная на промежутке [a;b] функция имеет на этом промежутке первообразную.
СВОЙСТВА НЕОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. (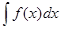 )’= f (x).
)’= f (x).
2. 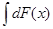 = F (x) + С.
= F (x) + С.
3. d 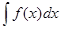 = f (x) dх.
= f (x) dх.
4. 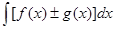 =
= 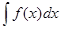
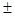
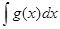 .
.
5. Если 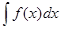 = F (x) + С и и =
= F (x) + С и и = 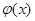 - произвольная функция, которая имеет непрерывную производную, то
- произвольная функция, которая имеет непрерывную производную, то
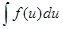 = F (и) + С.
= F (и) + С.
В частности,
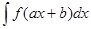 =
= 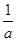 F (a x+b) + С.
F (a x+b) + С.
Из очень важного свойства 5 следует, что таблица интегралов остаётся верной независимо от того, является ли переменная интегрирования независимой переменной или произвольной дифференцированной функцией. Таким образом, из одной формулы можно получать много других.
Пример.
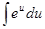 =
= 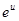 + С
+ С 
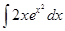 =
= 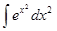 =
=  + С,
+ С, 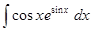 =
= 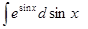 =
= 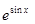 + С,
+ С, 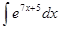 =
= 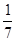
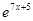 + С.
+ С.
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
1. 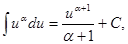
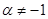 .
.
2. 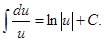
3. 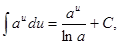 а >0,
а >0, 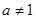 .
.
4. 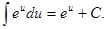
5. 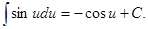
6. 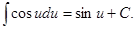
7. 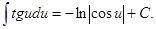
8. 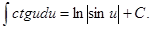
9. 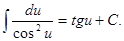
10. 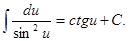
11. 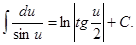
12. 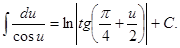
13. 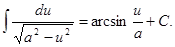
14. 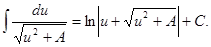
15. 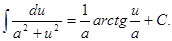
16. 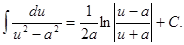
17. 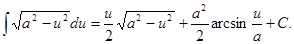
18. 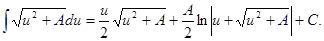
Непосредственным интегрированием называют вычисление интегралов с помощью основных свойств неопределённого интеграла и таблицы интегралов.
Пример.
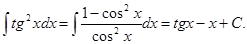
Метод подстановки является одним из основных методов интегрирования. Больше того, изучение методов интегрирования в основном сводится к выяснению того, какую подстановку надо сделать в том или ином случае.
Пример.
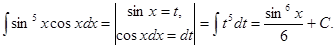
Этот пример можно было бы решить и так:
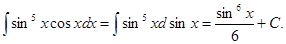
Такой метод интегрирования называется методом введения функции под знак дифференциала.
3. Пусть и (х), v (x) – функции, которые имеют на некотором промежутке непрерывные производные. Тогда
d (uv) = udv + vdu
или
udv= d (uv) – vdu.
Интегрируя это равенство, получим

или, учитывая свойство 2 неопределённых интегралов,
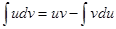 .
.
Эту формулу называют формулой интегрирования по частям.
Укажем некоторые интегралы, которые удобно вычислять методом интегрирования по частям:
1) в интегралах 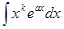
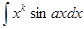
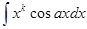 , где k – натуральное число, за и следует брать хk, а за dv – выражение, которое осталось;
, где k – натуральное число, за и следует брать хk, а за dv – выражение, которое осталось;
2) в интегралах 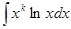
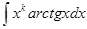
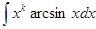
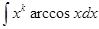 , следует обозначать dv= хkdx.
, следует обозначать dv= хkdx.
Неопределённый интеграл существует для произвольной непрерывной функции f (x), то есть 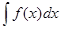 = F (x) + С. Но при этом не всегда первообразная F (x) является элементарной функцией. О таких интегралах говорят, что они ”не берутся”. Например,
= F (x) + С. Но при этом не всегда первообразная F (x) является элементарной функцией. О таких интегралах говорят, что они ”не берутся”. Например,
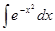 = F (x) + С, где F (x) = х -
= F (x) + С, где F (x) = х - 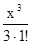 +
+ 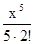 -
- 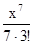 +....
+....
Не берутся такие интегралы:
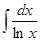 - интегральный логарифм,
- интегральный логарифм, 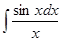 - интегральный синус,
- интегральный синус, 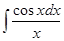 - интегральный косинус,
- интегральный косинус, 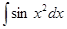 ,
, 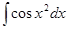 - интегралы Френеля и другие.
- интегралы Френеля и другие.
В связи с этим важно выделить такие классы функций, интегралы от которых всегда выражаются через элементарные функции. Одним из таких классов функций, интегралы от которых всегда ”берутся”, является класс рациональных функций.
Лекция 13. Тема – Элементарные дроби и их интегрирование. Интегрирование некоторых иррациональных и тригонометрических функций.
План.
Date: 2015-07-27; view: 502; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |