
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Глава 1. История возникновения уравнений
|
|
Представим, что в очень легком – практически невесомом – кошельке содержится какое-то количество монет одинакового достоинства. Как узнать, сколько монет в кошельке, не заглядывая внутрь? Есть очень простой способ: положим кошелек на одну чашу рычажных весов и уравновесим его монетками на другой чаше. Сколько монет для этого потребуется – столько же их и в кошельке.
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах, содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов." Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37…", - поучал во втором тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели каким-то общими приемами решения задач с неизвестными величинами. Однако, ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: " Смотри!", " Делай так!", " Ты правильно нашел". В этом смысле исключением является "Арифметика" греческого математика Диофанта Александрийского – собрание задач на составление уравнений с систематическим изложением их решений.
Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда Бен Мусы аль-Хорезми. Слово "аль-джебр" из арабского названия этого трактата – "Китаб аль-джебр Валь-мукабала" (" Книга о восстановлении и противопоставлении") – со временем превратилось знакомое всем слово "алгебра". А само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
Аль-Хорезми один из первых стал обращаться с уравнениями так, как торговец обращается с рычажными весами. Пусть, например, имеет равенство 5 х – 16=20 – 4 х. Считая, что оно задает равновесие некоторых грузов на чашах весов, торговец вправе заключить, что равенство не изменится, если он на обе чаши добавит одно и то же количество:
| было | 5х – 16=20 – 4х, |
| добавил | + 16+16, |
| стало | 5х = 36 – 4х. |
После этой законной операции прибавления одинаковых количеств число 16 исчезло из левой части исходного равенства, зато со значением плюс оно возникло (восстановилось) в правой части. Точно также на обе чаши весов можно добавить одно и то же количество 4х:
| было | 5х=36 – 4х, |
| добавил | +4х +4х, |
| стало | 9х=36. |
Опять из правой части равенства выражение 4х пропало, а в левой оно восстановилось со знаком плюс. Из полученного простого равенства 9х=36 уже легко вычислить что х=4.
Восстановлением ("аль-джебр") аль-Хорезми назвал операцию исключения из обеих частей уравнения вычитаемых членов путем добавления противоположных по знаку. Противопоставление ("аль-мукабала") – это сокращение в частях уравнения одинаковых членов.
Взгляд уравнения как на равенство грузов на весах, на обеих чашах которых можно производить одинаковые преобразования, оказался очень плодотворным. Равные количества можно не только прибавлять к обеим частям уравнения или вычитать из них. Равенство не нарушится и тогда, когда обе части умножаются или делятся на одно и то же число (разумеется, если оно не нуль). Главный принцип: если над равным количеством произвести одинаковые действия, то в результате снова получаются равные количества – стал своеобразной "волшебной палочкой", которую обнаружили вдумчивые читатели руководства аль-Хорезми. Однако "палочкой" этой нужно пользоваться с осторожностью.
В сочинении аль-Хорезми неизвестные величины, так же как и все сопутствующие выкладки и преобразования уравнений, выражались словесно.
Такой стиль изложения, характерный для раннего этапа развития алгебры, историки науки называют риторическим (красноречивым).
Новый великий прорыв в алгебре связан с именем французского ученого XVI в. Франсуа Виета. Он первым из математиков ввел буквенные обозначения для коэффициентов уравнения и неизвестных величин. А традицией обозначать неизвестные величины последними буквами латинского алфавита (х, y или z) мы обязаны соотечественнику Виета – Рене Декарту.
Изобретение Виета позволило гораздо легче находить самые общие решения для многих, похожих одна на другую задач. Предположим, со станции, находящейся в 160 км от Москвы, в направлении от столицы выезжает поезд со скоростью 85 км/ч. Через какое время он окажется на расстоянии 500 км от Москвы? Как изменится решение, если поезд отправляется со станции, удаленной на 359 км от столицы, а скорость его движения 70 км/ч? Эти две задачи отличаются лишь исходными данными, поэтому допускают запись условия в общем виде. Если поезд отправляется из пункта, расположенного в а км от Москвы, в противоположную от него сторону со скоростью v км/ч, то для того, чтобы достичь расстояния b км от столицы, ему понадобится время t. Условие выражается уравнением
а+ vt=b.
Решая это уравнение относительно неизвестного t, находим
t = 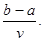
Это общая формула, которая охватывает все частные случаи для конкретных числовых параметров a,b,v. Например, полагая а=160 км, b=500км, v=85 км/ч, получаем
t= 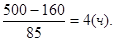
Если же а=395 км, b=500 км, v= 70 км/ч, то
t= 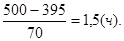
Формула одна, а решения разные. Поистине "математика – это искусство давать различным вещам одно и то же название". Этот остроумный и глубокий афоризм принадлежит Анри Пуанкаре, создателю многих современных областей математики. В работе "Наука и метод" Пуанкаре особо выделял способность ученого не просто видеть голые факты, а заглядывать гораздо глубже – познавать душу фактов, производить обобщения: "Простым примером является алгебраическая формула, которая дает нам решение всех численных задач определенного типа, так что достаточно лишь заменить буквы числами. Благодаря такой формуле алгебраическое вычисление, однажды выполненное, избавит нас от необходимости повторять без конца все новые и новые численные выкладки".
Слова Пуанкаре необычайно актуальны в наш век всеобщего триумфа компьютерной техники. Умницы- компьютеры научились понимать язык алгебраических формул и способны перерабатывать (т.е. вычислять по этим формулам) огромные массивы числовых данных. Нужно только подбирать и вводить исходные числа, чтобы получить готовые ответы.
Date: 2015-07-25; view: 7770; Нарушение авторских прав