
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Выбор с возвращением и без учёта порядка
Рассмотрим урну с двумя пронумерованными шарами и перечислим результаты выбора двух шариков из этой урны при выборе с возвращением.
| с учётом порядка | без учёта порядка |
| (1,1) | (1,1) |
| (2,2) | (2,2) |
| (1,2) (2,1) | } (1,2) |
Видим, что в схеме «без учёта порядка» получилось три различных результата, в отличие от четырёх результатов в схеме «с учётом порядка». Заметим также, что никаким делением на «число каких-нибудь перестановок», которое помогло избавиться от учёта порядка при выборе без возвращения, число 3 из числа 4 получить не удастся.
Теорема 5. Общее количество различных наборов при выборе 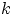 элементов из
элементов из  с возвращением и без учёта порядка равняется
с возвращением и без учёта порядка равняется
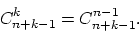
Упражнение 6. Проверить, что при 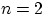 и
и  получается ровно 3.
получается ровно 3.
Доказательство. Рассмотрим подробно, чем отличаются друг от друга два разных результата такой схемы выбора. Нам не важен порядок номеров, т.е. мы учитываем только, сколько раз в нашем наборе из 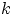 номеров шаров появился каждый номер. Поэтому результат выбора можно представить набором чисел
номеров шаров появился каждый номер. Поэтому результат выбора можно представить набором чисел 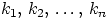 , в котором
, в котором 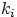 — число появлений шара номер
— число появлений шара номер 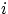 в наборе, и
в наборе, и 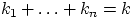 . Числа
. Числа 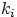 принимают значения из
принимают значения из 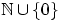 . Два результата выбора в схеме выбора с возвращением и без учёта порядка различаются, если соответствующие им наборы
. Два результата выбора в схеме выбора с возвращением и без учёта порядка различаются, если соответствующие им наборы 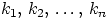 не совпадают (порядок следования элементов
не совпадают (порядок следования элементов 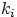 учитывается).
учитывается).
Представим себе другой эксперимент, имеющий точно такие же результаты, и посчитаем их количество. Есть  ящиков, в которых размещаются
ящиков, в которых размещаются 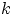 шаров. Нас интересует только число шаров в каждом ящике. Результатом эксперимента снова является набор чисел
шаров. Нас интересует только число шаров в каждом ящике. Результатом эксперимента снова является набор чисел 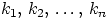 , где
, где 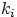 равно числу шаров в ящике с номером
равно числу шаров в ящике с номером 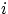 , и
, и 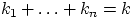 . Числа
. Числа 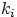 принимают натуральные значения или равны нулю.
принимают натуральные значения или равны нулю.
А теперь изобразим результат такого размещения в виде схемы, в которой вертикальные линии обозначают перегородки между ящиками, а точки — находящиеся в ящиках шары:

Мы видим результат размещения девяти шаров по семи ящикам. Первый ящик содержит три шара, второй и шестой ящики пусты, третий ящик содержит один шар, в четвёртом и пятом ящиках лежит по два шара. Переложим один шар из первого ящика во второй и изобразим таким же образом ещё два результата размещения:


Видим, что все размещения можно получить, меняя между собой шары и перегородки, или расставляя 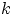 шаров на
шаров на 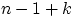 местах. Число
местах. Число 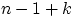 получается так: у
получается так: у  ящиков есть ровно
ящиков есть ровно 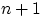 перегородка, считая крайние, но из них перемещать можно лишь
перегородка, считая крайние, но из них перемещать можно лишь 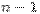 внутреннюю перегородку. Таким образом, имеется
внутреннюю перегородку. Таким образом, имеется 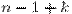 мест, которые можно занять шарами либо внутренними перегородками. Перебрав все возможные способы расставить
мест, которые можно занять шарами либо внутренними перегородками. Перебрав все возможные способы расставить 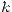 шаров на этих
шаров на этих 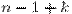 местах (заполняя оставшиеся места перегородками), переберем все нужные размещения.
местах (заполняя оставшиеся места перегородками), переберем все нужные размещения.
Осталось заметить, что способов расставить 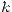 шаров на
шаров на 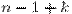 местах существует
местах существует
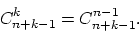
Именно столько есть способов выбрать из 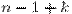 номеров мест
номеров мест 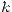 номеров мест для шаров.
номеров мест для шаров.
Date: 2015-07-02; view: 903; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |