
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема сложения для совместных событий
Суммой 2-х совместных событий называют событие, состоящее в появлении либо события A, либо события B, либо обоих сразу.
Теорема. Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без учета их совместного появления. p(A+B)=p(A)+p(B)−p(AB)
Доказательство:
A+B=AB+AB+AB (сумма несовместных пар)
Тогда p(A+B)=p(AB)+p(AB)+p(AB)
Событие A=AB+AB,
Событие B=AB+AB
p(A+B)=p(A)−p(AB)+p(B)−p(AB)+p(AB)=p(A)+p(B)−p(AB)
Замечание: в этой теореме может существовать 2 различные ситуации.
p(A+B)=p(A)+p(B)−p(A)p(B), где A и B - независимые;
p(A+B)=p(A)+p(B)−p(A)p(B∖A), где A и B - зависимые;
Теоремы о вероятностях. Теоремы сложения несовместных событий.
Суммой 2-х несовместных событий A+B называется событие, состоящее в появлении либо события А, либо события B.
Теорема. Вероятность суммы 2-х несовместных событий равна сумме вероятностей этих событий p(A+B)=p(A)+p(B)
Доказательство.
Если n - общее число всех элементарных исходов;
m1 -- число исходов благоприятных событию A;
m2 -- число исходов благоприятных событию B;
p(A+B)=nm1+m2=nm1+nm2=p(A)+p(B)
Теорема. Вероятность суммы нескольких парно несовместных событий равна сумме вероятностей этих событий.
Доказательство проводится методом математической индукции.
Теорема. Сумма вероятностей событий, образующих полную группу равна 1.
p(A1)+...+p(Ak)=1
Доказательство. Согласно теореме p(A1+A2+...Ak)=p(A1)+p(A2)+...p(Ak).
Так как события Ai образуют полную группу, то сумма событий A1+A2+...Ak есть достоверное событие (хотя бы одно произойдет).
Следовательно, p(A1+A2+...Ak)=1, а потому p(A1)+...+p(Ak)=1.
ЧТД
Теорема. Сумма вероятностей противоположных событий равна 1. p(A)+p(A)=1
Доказательство производится на основании предыдущей теоремы, так как эти события образуют полную группу, несовместны.
Множества и операции над множествами
Напомним основные обозначения, понятия, относящиеся к множествам, которых будем придерживаться дальше.
Начнем с основного понятия, которое встречается практически в каждом разделе математики - это понятие множества.
Множество - это совокупность, набор элементов, объединенных общими свойствами.
Множества обозначаются заглавными латинскими буквами 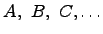 , а элементы множества строчными латинскими буквами
, а элементы множества строчными латинскими буквами 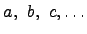 .
.
Запись 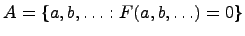 означает, что есть множество
означает, что есть множество 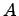 с элементами
с элементами  , которые связаны между собой какой-то функцией
, которые связаны между собой какой-то функцией 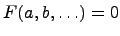 .
.
Замечание. Элементы в множество входят по одному разу, т.е. без повторений.
Основные операции:
1. Принадлежность элемента множеству:
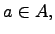
где 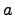 -- элемент и
-- элемент и 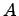 -- множество (элемент
-- множество (элемент 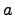 принадлежит множеству
принадлежит множеству 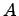 ).
).
2. Непринадлежность элемента множеству:
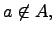
где 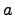 -- элемент и
-- элемент и 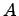 -- множество (элемент
-- множество (элемент 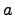 не принадлежит множеству
не принадлежит множеству 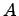 ).
).
3. Объединение множеств: 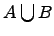 .
.
Объединением двух множеств 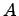 и
и 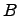 называется множество
называется множество 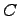 , которое состоит из элементов множеств
, которое состоит из элементов множеств 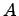 и
и 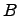 , т.е.
, т.е.
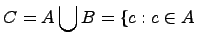 или
или 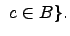
4. Пересечение множеств: 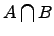 .
.
Пересечением двух множеств 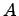 и
и 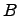 называется множество
называется множество 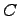 , которое состоит из общих элементов множеств
, которое состоит из общих элементов множеств 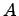 и
и 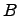 , т.е.
, т.е.
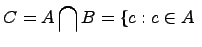 и
и 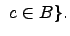
5. Разность множеств: 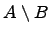 .
.
Разностью двух множеств 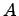 и
и 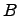 , например, множество
, например, множество 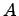 минус множество
минус множество 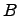 , называется множество
, называется множество 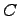 , которое состоит из элементов множества
, которое состоит из элементов множества 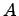 , которых нет в множестве
, которых нет в множестве 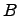 , т.е.
, т.е.
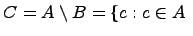 и
и 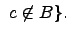
6. Симметрическая разность множеств: 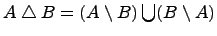 .
.
Симметрической разностью двух множеств 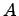 и
и 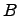 называется множество
называется множество 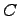 , которое состоит из не общих элементов множеств
, которое состоит из не общих элементов множеств 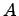 и
и 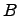 , т.е.
, т.е.
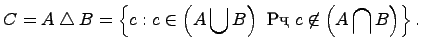
7. Дополнение множества: 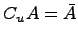 .
.
Если предположим, что множество 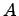 является подмножеством некоторого универсального множества
является подмножеством некоторого универсального множества 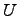 , тогда определяется операция дополнения:
, тогда определяется операция дополнения:
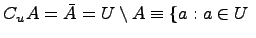 и
и 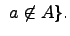
8. Вхождение одного множества в другое множество: 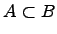 .
.
Если любой элемент множества 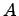 является элементом множества
является элементом множества 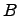 , то говорят, что множество
, то говорят, что множество 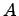 есть подмножество множества
есть подмножество множества 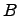 (множество
(множество 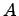 входит в множество
входит в множество 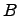 ).
).
9. Не вхождение одного множества в другое множество: 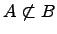 .
.
Если существует элемент множества 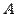 , который не является элементом множества
, который не является элементом множества  , то говорят, что множество
, то говорят, что множество 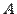 не подмножество множества
не подмножество множества  (множество
(множество 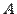 не входит в множество
не входит в множество  ).
).
Date: 2015-07-02; view: 442; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |