Кеңістіктегі түзудің жалпы теңдеуі

Түзуді екі жазықтықтыңтың қиылысу арқылы былай анықталады: 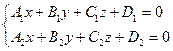. Бұлардың нормаль ваекторларының координаталары былайша анықталады: 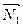(A₁, B₁, C₁), 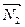(A₂, B₂, C₂);

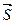
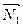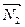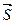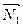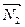Түзудің бағыттауыш векторы , векторларына перпендикуляр. Сонда = x Þ .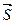

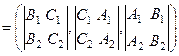Жазықтық векторлық формада төмендегі теңдеу арқылы берілуі мүмкін:

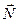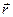× + D = 0, где

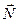- жазықтықтың нормалі; 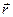-Жазықтықтың кез келген нүктесінің радиус - векторы.

Айталық кеңістікте екі жазықтық берілсін: 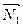× 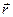+ D₁ = 0 и 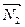× 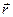+ D₂ = 0,нормаль векторлардың координаталары:: 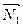(A₁, B₁, C₁), 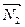(A₂, B₂, C₂); 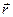(x, y, z).

Түзудің жалпы теңдеуі параметрлік түрде беріледі:

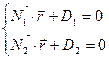
Түзудің координаталық формадағы жалпы теңдеуі:

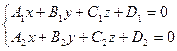
Бұл практика жүзінде есеп теңдеуі жалпы түрде берілген түзулердің теңдеулерін канондық түрге келтіру болып табылады.

Ол үшін түзудің кез келген нүктесін және m, n, p сандарын табады.

Бұл ұшін түзудің бағыттаушы векторы берілген жазықтықтардың нормаль векторлардың векторлық көбейтіндісі арқылы анықталады.

Мысалы. Түзудің 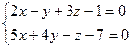канондық теңдеуін тап.

Түзудің кез келген нүктесін табу үшін х = 0 деп аламыз, содан кейін осы мәнді берілген теңдеулер жүйесіне қоямыз.

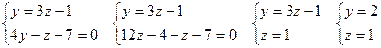, т.е. А(0, 2, 1).

Түзудің бағыттаушы векторының компоненттерін табамыз:

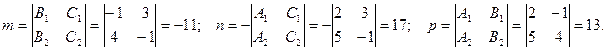
Сонда түзудің канондық теңдеуі:

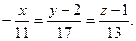
Мысал.

Түзудің 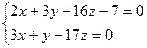теңдеуін канондық (жабайы) түрге кеклтір.

Жоғарыдағы екі жазықтықтың қиылысуы арқылы берілген тұзудің кез келген нүктесін табу үшін z = 0 деп аламыз.Сонда:

;

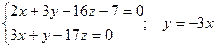2x – 9x – 7 = 0;

x = -1; y = 3;

Сонымен: A(-1; 3; 0).

Түзудің бағыттаушы векторы: .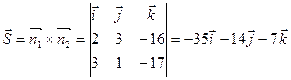

Сонымен: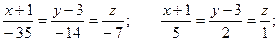

Date: 2015-07-01; view: 3285; Нарушение авторских прав