
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Алгебралық толықтауыштар мен минорлар
Анықтама. Үшінші ретті анықтауыштың аij элементінің Мij миноры деп анықтауыштың і - ші жатық жолын және j - ші тік жолын сызғанда калған элементтерінен құралған екінші ретті анықтауышты атайды.
Мысалы, М23= 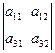
Анықтама. аij элементінің Aij алгебралық толақтауышы деп оның (-1)i+j таңбасымен алынған минорын айтады, яғни Аij=(-1)i+j 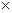 Mij.
Mij.
Мысал. Мына анықтауыштың  М12, М31, А22, А12 табу керек.
М12, М31, А22, А12 табу керек.
М12= 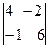 =24-2=22, М31=
=24-2=22, М31= 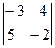 =6-20=-14,
=6-20=-14,
A22=(-1)2+2 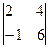 =+(12+4)=16, A12=(-1)1+2
=+(12+4)=16, A12=(-1)1+2 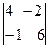 =-(24-2)=-22.
=-(24-2)=-22.
Екі және үш белгісізді сызықтық теңдеулер жүйесі. Крамер формулалары.
Бізге үш белгісізді сызықтық үш тендеулер жүйесі берілсін:
 a11x1+ a12x2+a13x3=b1
a11x1+ a12x2+a13x3=b1
a21x1+ a22x2+a23x3=b2
a31x1+ a32x2+a33x3=b3
Мұндағы аij коэффициентері мен bi босмүшелері нақты сандар болсын. Мына белгілеулерді енгізейік
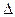 =
=  ,
, 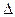 =
= 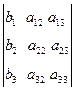 ,
,  =
= 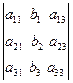 ,
,  =
= 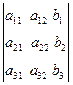
Егер 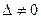 , онда Крамер ережесі бойынша
, онда Крамер ережесі бойынша 
Мысал. Мына жжүйенің шешімін Крамер формулаларын қолданып табу керек

Шешемі. Анықтауыштарын есептейміз 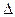 =
= 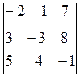 =290,
=290, 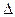 1=
1=  =580,
=580, 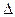 2=
2= 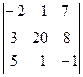 =-580,
=-580, 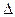 3=
3=  =290
=290
Сонымен,  , яғни (2;-2;1) үштегі қарастырылып отырған теңдейлер жүйесінің шешімі болады.
, яғни (2;-2;1) үштегі қарастырылып отырған теңдейлер жүйесінің шешімі болады.
Date: 2015-07-01; view: 4654; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |