Модель непрерывного замедления. Возраст нейтронов

В гл. 2 была рассмотрена диффузия моноэнергетических нейтронов (подразумевались тепловые) в среде конечных размеров. Обмен энергий с ядрами при этом не учитывался, и все нейтроны имели одну и ту же энергию после любого числа столкновений. В дальнейшем (гл. 3) рассматривалось замедление нейтронов в бесконечной однородной и гомогенной среде с равномерно распределенными источниками, т. е. в отсутствие диффузии нейтронов. Такое изложение в первую очередь обусловлено стремлением более наглядно представить физическую сущность процессов диффузии и замедления. Необходимо также отметить, что в чаще всего преобладающую роль играет лишь один из этих процессов. Тем не менее, при вычислении распределения плотности нейтронов ядерном реакторе нельзя разделять процессы диффузии и замедления.

Конечно, было бы желательно неким образом совместить эти модели. Существует несколько способов нахождения пространственного распределения замедляющихся нейтронов. Вначале остановимся на сравнительно простом, основанном на модели непрерывного замедления.

Суть этой модели удобно выяснить с помощью рис. 3.5, на котором представлена качественная зависимость 1n (E_f/E) от времени t.

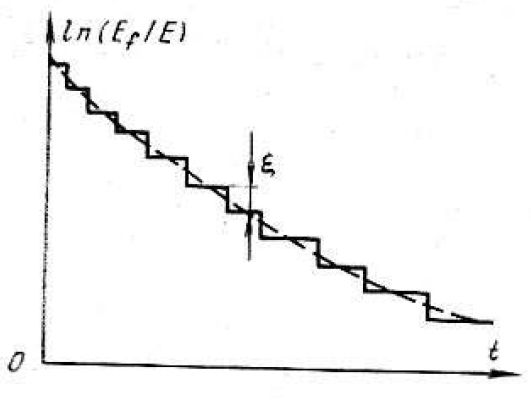
Рис. 3.5 Зависимость 1n (E_f/E) от времени t

Эта зависимость имеет ступенчатый вид. Высота ступенек постоянна почти во всем интервале энергии замедляющихся нейтронов и равна средней логарифмической потере энергии на одно столкновение. При замедлении во всех средах, кроме водородсодержащих, нейтрон испытывает много соударений прежде чем станет тепловым. В таких средах высота ступенек мала, поэтому реальную зависимость с хорошей точностью можно заменить плавной (штриховая кривая на рис. 3.5). Таким образом, основное допущение данной модели заключается в том, что процесс замедления считается непрерывным.

Итак, использовав модель непрерывного замедления, получим уравнение, описывающее пространственное распределение замедляющихся нейтронов. Рассмотрим простейший случай.когда поглощение нейтронов в процессе замедления отсутствует (Σ_a=0), а источник испускает моноэнергетические нейтроны с энергией E_f. Даже если все нейтроны образуются с одинаковой энергией, они не будут обладать одной и той же энергией по истечении некоторого времени с момента рождения из-за статистического характера процесса рассеяния. Другими словами, график зависимости 1n (E_f/E) от времени t (рис. 3.5) меняется от нейтрона к нейтрону. Поyятно, что этот разброс нейтронов по энергиям в любой момент времени будет тем меньше, чем более тяжелые ядра используются в качестве замедлителя.

Примем, что все нейтроны, диффундировавшие в течение времени t после рождения, имеют скорость v. Тогда число столкновений, испытываемых одним нейтроном за время dt, равно vdt/λ_s. В то же время число столкновений нейтрона в интервале энергии dE есть dE/ ζE, а в шкале летаргии (du/ ζ).

Иначе говоря, мы связываем через число столкновений dn переменные времени и энергии(летаргии):

vdt/λ_s< =dn=>du/ ζ

При отсутствии источников и поглощения нейтронов уравнение диффузии для плотности нейтронов n(r,t) примет вид:

DvΔn(r, t)=- дп(r,t)/dt

Имея связь времени t с летаргией u перейдем в последнем уравнении от плотности n(r, t) к плотности n(r, и). Поскольку

n(r,t)dt=n(r,u)du

и якобиан преобразования du/dt= ζ v/λ_s=v ζ*Σ_s получим

DΔ[ζ*Σ_s Ф(r,u)]= ζ*Σ_s ∂[ ζ*Σ_sФ(r,u)]/ ∂u (3.12a)

Здесь Ф(г, u)=vn(r,u)- поток нейтронов на единицу интервала летаргии. Величина, стоящая в квадратных скобках, есть плотность замедления q(r, и) - плотность замедления в среде без поглощения.

q(r, и)= ζ*Σ_sФ(r,u)] (3.12b)

Ее по-другому называют поток нейтронов по энергетической оси – это другое определение – плотность замедления нейтронов или поток нейтронов по энергетической оси.

Теперь вместо летаргии и введем новую независимую переменную, называемую возрастом нейтронов:

τ(u) = 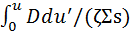(3.13a)

Эквивалентное определение в дифференциальной форме:

dτ(u)/du = 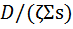(3.13б)

Тогда уравнение (3.12) запишется в виде:

Δq(r, τ)=∂q(r, τ)/∂ τ (3.14а)

Это уравнение и называется уравнением возраста(в среде без поглощения).

В среде с источниками оно примет вид

Δq(r, τ)=∂q(r, τ)/∂τ +S(r) δ(τ) (3.14б)

где S(r) —скорость генерации нейтронов в единицу времени и в единице объема; δ(τ) -дельта-функция Дирака. Отметим, что уравнение возраста по своему виду совпадает с нестационарным уравнением теплопроводности, решения которого достаточно хорошо известны. Собственно, сведение нейтронно-физических уравнений к виду хорошо изученных и было целью построения данной модели.

Для сред с поглощением математический аппарат усложняется, но смысл основных понятий не меняется.

Для сред и источников вводятся специальные граничные условия.

Возраст нейтронов τ был введен чисто формально при выводе уравнений возраста и замедления и определяется выражением (3.13а-б).

Однако он имеет и физический смысл и, более того, его можно измерить в эксперименте.

Физический смысл. На рис. 3.6 показано распределение плотности замедления j(r, τ) вблизи точечного источника (τ₁< τ ₂< τ ₃).

Для каждого значения τ имеет место гауссова кривая с максимумом S_T/(4n τ)^3/2в точке, где расположен источник. Поэтому, когда возраст τ мал (энергия нейтронов близка к энергии нейтронов источника), кривая оказывается высокой и узкой. По мере замедления нейтронов (τ увеличивается) кривая становится более низкой и размытой. Такого характера кривых следует ожидать и из физических соображений. Нейтроны больших энергий (кривая τ₁) испытали в среде мало столкновений и не успели продиффунднровать далеко от источника. Нейтроны, замедлившиеся до низких энергий (большие τ), испытали много столкновении, успели продиффунднровать на значительные расстояния и распределены в среде более или менее равномерно (кривая τз). Естественно, площадь под кривой при всех значениях т остается постоянной. Это означает, что число нейтронов всех энергий в единицу времени одинаково и равно S_T.

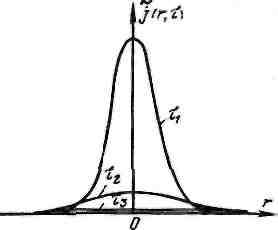
Рис. 3.6 Распределение плотности замедления j(r, τ) вблизи точечного источника (τ₁< τ ₂< τ ₃).

Средний квадрат расстояния, на которое смещается нейтрон при замедлении от источника равно:

<r² (τ)> =6 τ

Следовательно, возраст нейтронов есть 1/6 среднего квадрата расстояния (по прямой), на которое смещается нейтрон при замедлении от энергии источника (соответствующего нулевому возрасту) до данной энергии, отвечающей возрасту τ.

Date: 2015-07-01; view: 1824; Нарушение авторских прав