Критерии надежности восстанавливаемых изделий

Пусть на испытании находится N изделий и пусть от­казавшие изделия немедленно заменяются исправными (новыми или отремонтированными). Испытания счита­ются законченными, если число отказов достигает вели чины, достаточной для оценки надежности с определенной доверительной вероятностью. Если не учитывать времени, потребного на восстановление системы, то ко­личественными характеристиками надежности могут быть параметр потока отказов μ(t) и наработка на от­каз Т.

Параметром потока отказов называется отношение числа отказавших изделий в единицу времени к числу испытываемых изделий при условии, что все вышедшие из строя изделия заменяются исправными (новыми или отремонтированными).

Согласно определению

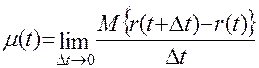, (14.17)

где ∆t – малый отрезок наработки, r(t)- число отказов, наступивших от начального момента времени до достижения наработки t. Разность r(t+∆t) – r(t) представляет собой число отказов на отрезке ∆t.

Статистическую оценку параметра потока отказов дают по формуле:

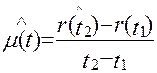. (14.18)

Для стационарных потоков можно применять формулу:

, (14.19)

где 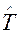- оценка средней наработки на отказ по формуле (8)?:

, здесь t - суммарная наработка, r(t) – число отказов, наступивших в течение этой наработки, 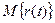- математическое ожидание этого числа.

Параметр потока отказов определяется также по формуле:

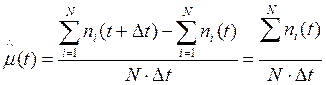(14.20)

где n(∆t) —число отказавших образцов в интервале вре­мени от t — ∆t/2 до '/+∆ t /2; N — число испытываемых об­разцов; ∆t — интервал времени.

Выражение (1.13) является статистическим определе­нием параметра потока отказов.

Параметр потока отказов и частота отказов для орди­нарных потоков с ограниченным последействием связаны интегральным уравнением Вольтерра второго рода

μ(t)==f(t) + 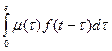(14.21)

По известной f(t) можно найти все количественные характеристики надежности невосстанавливаемых изде­лий. Поэтому (14.21) является основным уравнением, свя­зывающим количественные характеристики надежности невосстанавливаемых и восстанавливаемых изделий при мгновенном восстановлении.

Уравнение (14.21) можно записать в операторной форме:

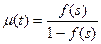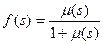, . (14.22)

Соотношения (14.22) позволяют найти одну характе­ристику через другую, если существуют преобразования Лапласа функций a(s) и m(s) и обратные преобразова­ния выражений (14.22).

Параметр потока отказов обладает следующими важ­ными свойствами:

1) для любого момента времени независимо от зако­на распределения времени безотказной работы параметр потока отказов больше, чем частота отказов,

т. е. μ(t) >>f(t);

2) независимо от вида функции f(t) параметр пото­ка отказов μ(t) при t → ∞ стремится к 1/Т_ср. Это важ­ное свойство параметра потока отказов означает, что при длительной эксплуатации ремонтируемого изделия' поток его отказов независимо от закона распределения вре­мени безотказной работы становится стационарным. Од­нако это не означает, что интенсивность отказов
есть величина постоянная;

3) если l(t) —возрастающая функция времени, то
l(t) > μ(t)>f(t),

4) если l(t)—убывающая функция, то
f(t)> l(t) > μ(t);

5) при l(t)= eonst параметр лотока отказов системы
не равен сумме параметров потоков отказов элементов,
т. е.

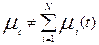(14.23)

Согласно этому свойству параметра потока отказов можно утверждать, что при вычислении количественных харак­теристик надежности сложной системы нельзя суммиро­вать имеющиеся в настоящее время значения интенсивностей отказов элементов, полученные по статистиче­ским данным об отказах изделий в условиях эксплуата­ции, так как указанные величины являются фактически параметрами потока отказов;

6) при l(t) = l = const параметр потока отказов равен
интенсивности отказов μ(t) = l(t) =l.

Сравнение свойств интенсивности и параметра потока отказов показывает, что эти характеристики различны.

В настоящее время широко используются статистиче­ские данные об отказах, полученные «в условиях эксплуа­тации аппаратуры. При этом они часто обрабатываются таким образом, что приводимые характеристики надеж­ности являются не интенсивностью отказов, а парамет­ром потока отказов μ(t). Это вносит ошибки при расче­тах надежности. В ряде случаев они могут быть значи­тельными.

Для получения интенсивности отказов элементов из статистических данных об отказах ремонтируемых систем необходимо воспользоваться формулой (1.6), для чего необходимо знать предысторию каждого элемента прин­ципиальной схемы. Это может существенно усложнить методику сбора статистических данных об отказах. По­этому целесообразно определять l(t) по параметру по­тока отказов μ(t). Методика расчета сводится к следую­щим вычислительным операциям:

- по статистическим данным об отказах элементов ремонтируемых изделий и по формуле (1.13)вычисляет­ся параметр потока отказов и строится гистограмма μ_i(t);

- гистограмма заменяется кривой, которая аппрокси­мируется уравнением;

- находится преобразование Лапласа μ_i (s) функции μ_i(t);

- по известной μ_i(s) на основании (1.15) записы­вается преобразование Лапласа f_i(s) частоты отказов,

- по известной f_i(s) находится обратное (преобразо­вание частоты отказов f_i(t);

- находится аналитическое выражение для интенсив­ности отказов по формуле

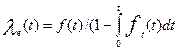(14.24)

- строится график l_i(t).

Если имеется участок, где l_i(t) = l = const, то посто­янное значение интенсивности отказов принимается для оценки вероятности безотказной работы. При этом счи­тается справедливым экспоненциальный закон надежно­сти.

Приведенная методика не может быть применена, ес­ли не удается найти по f(s) обратное преобразование частоты отказов f(t). В этом случае приходится приме­нять приближенные методы решения интегрального урав­нения (14.21) или машинные методы расчета.

Средней наработкой на отказ называется отношение суммарной наработки восстанавливаемого объекта к математическому ожиданиючисла его отказов в течение этой наработки.

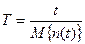, (14.25)

где t — суммарная наработка;

n(t) - число отказов, наступивших в течение этой наработки, М{n(t)} -математическое ожидание этого числа.

Статистически средняя наработка на отказ вычисляется по формуле 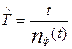, (14.26)

здесь n_ф(t) - число фактических отказов в течение наработки t.

Наработка на отказ является достаточно наглядной характеристикой надежности, поэтому она получила широкое распространение на практике.

Параметр потока отказов и наработка на отказ ха­рактеризуют надежность ремонтируемого изделия и не учитывают времени, потребного на его восстановление. Следовательно, они не характеризуют готовности изделия к вы­полнению своих функций в нужное время. Для этой це­ли вводятся такие критерии, как коэффициент готовности, и коэффициент вынужденного простоя.

Коэффициентом готовности называется вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течени6 которых применение объекта по неазначению не предусматривается.

Согласно данному определению

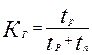(14.27)

где t_р — суммарное время работоспособного состояния объекта; t _п—суммарное время, в течение которого объект не использовался по назначению. Времена t_p и t _п вычисляются по формулам

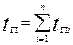(14.28)

где t _{р i} — время работы изделия между (i —1)-м и i -м отказом; t _п—время вынужденного простоя после i -го отказа; п — число отказов (ремонтов) изделия.

Выражение (14.27) является статистическим определе­нием коэффициента готовности. Для перехода к вероят­ностной трактовке величины t _ри t _nзаменяются математическими ожиданиями времени между соседними отка­зами и времени восстановления соответственно. Тогда

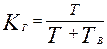(14.29)

где Т — наработка на отказ; Т_в — среднее время восста­новления.

Коэффициентом вынужденного простоя называется отношение времени вынужденного простоя к сумме вре­мен исправной работы и вынужденных простоев изделия, взятых за один и тот же календарный срок. Согласно определению

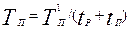(14.30)

или, переходя к средним величинам,

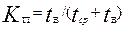(14.31)

Коэффициент готовности и коэффициент вынужденно­го простоя связаны между собой зависимостью

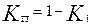(14.32)

При анализе надежности восстанавливаемых систем обычно коэффициент готовности вычисляют по формуле

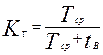(14.33)

Формула (14.31) верна только в том случае, если по­ток отказов простейший, и тогда t_cp = T.

Часто коэффициент готовности отождествляют с вероятностью того, что в любой момент времени восстанавливаемая система исправна. На самом деле указанные характеристики не­равноценны и могут быть отождествлены при определен­ных допущениях.

Действительно, вероятность возникновения отказа ре­монтируемой системы в начале эксплуатации мала. С ро­стом времени t эта вероятность возрастает. Это означает, что вероятность застать систему в исправном состоянии в начале эксплуатации будет выше, чем по истечении некоторого времени. Между тем на основании формулы (15.26)? коэффициент готовности не зависит от времени работы.

Для выяснения физического смысла коэффициента го­товности К_Г необходимо воспользоваться формулой для вероятности застать систему в исправном.состоянии. При этом рассматривается наиболее простой случай, когда интенсивность отказов и интенсивность восстановления есть величины постоян­ные.

Предполагая, что при t = 0 система находится в ис­правном состоянии (Р (0) = 1), вероятность застать систе­му в исправном состоянии можно определить из выражений

,

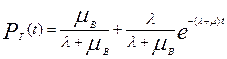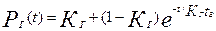, (14.34)

где

Т - средняя наработка на отказ, t _В – время восстановления,

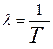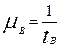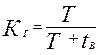, , . (14.35)

Это выражение устанавливает зависимость между ко­эффициентом готовности системы и вероятностью застать ее в исправном состоянии в любой момент времени t.

Из (14.34) видно, что P_Г(t) → К_Г при t → ∞, т. е. практически коэффициент готовности имеет смысл веро­ятности застать объект в исправном состоянии при уста­новившемся процессе эксплуатации.

В некоторых случаях критериями надежности восста­навливаемых систем могут быть также критерии надеж­ности невосстанавливаемых систем, например: вероят­ность безотказной работы, частота отказов, средняя на­работка до первого отказа, интенсивность отказов. Такая необходимость возникает всегда, когда имеет смысл оце­нить надежность восстанавливаемой системы до первого отказа, а также в случае, когда применяется резервиро­вание с восстановлением отказавших резервных устройств в процессе работы системы, причем отказ всей резерви­рованной системы не допускается.

Date: 2015-07-17; view: 3562; Нарушение авторских прав