
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач. Предлагается несколько простых примеров решения задач
Предлагается несколько простых примеров решения задач. Следует помнить, что частота, интенсивность отказов и параметр потока отказов, вычисленные по формулам (14.35), (14.6) и (14.13), являются постоянными в диапазоне интервала времени ∆t, а функции 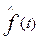 ,
, 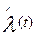 ),
), 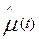 —ступенчатыми кривыми или гистограммами. Для удобства изложения в дальнейшем при решении задач на определение частоты, интенсивности и параметра потока отказов по статистическим данным об отказах изделий ответы относятся к середине интервала ∆t. При этом результаты вычислений графически представляются не в виде гистограмм, а в виде точек, отнесенных к середине интервалов ∆ti и соединенных плавной кривой.
—ступенчатыми кривыми или гистограммами. Для удобства изложения в дальнейшем при решении задач на определение частоты, интенсивности и параметра потока отказов по статистическим данным об отказах изделий ответы относятся к середине интервала ∆t. При этом результаты вычислений графически представляются не в виде гистограмм, а в виде точек, отнесенных к середине интервалов ∆ti и соединенных плавной кривой.
Пример.1
Допустим, что на испытание поставлено 1000 однотипных электронных ламп. За 3000 ч отказало 80 ламп, требуется определить вероятность безотказной работы P(t) и вероятность отказа Q(t) в течение 3000 ч.
| Дано: N = 1000 шт ∆t = 3000 ч n = 80 шт | Решение:
P(t) = 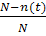 ;
P(t) = ;
P(t) = 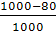 = 0,92;
Q (3000) = 1 – P (3000) = 0,08 или Q (3000) = = 0,92;
Q (3000) = 1 – P (3000) = 0,08 или Q (3000) = 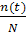 = =  = 0,08 = 0,08
|
| Найти: P(t), Q(t) |
Пример 2
Допустим, что на испытание поставлено 1000 однотипных электронных ламп. За первые 3000 ч отказало 80 ламп, а за интервал времени 3000-4000 ч отказало еще 50 ламп. Требуется определить частоту f(∆t) и интенсивность λ(∆t) отказов электронных ламп в промежутке времени ∆t = 3000 … 4000 ч.
| Дано: N = 1000 шт. ∆t1 = 3000 ч n1 = 80 шт. ∆t2 = [3000,4000] n2 = 50 шт. | Решение:
f(∆t2) = 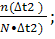 f(∆t2) = f(∆t2) = 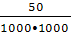 = 5•10-5 ч-1;
λ(∆t2) = = 5•10-5 ч-1;
λ(∆t2) = 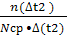 ;
Nср = ;
Nср = 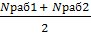 ;
Nраб1 = 1000 – 80 = 920 шт;
Nраб2 = 1000 – 130 = 870 шт
Nср = ;
Nраб1 = 1000 – 80 = 920 шт;
Nраб2 = 1000 – 130 = 870 шт
Nср = 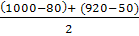 = 895;
λ(∆t2) = = 895;
λ(∆t2) = 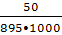 = 5,58 •10-5 ч-1; = 5,58 •10-5 ч-1;
|
| Найти: a(∆t2), λ(∆t2) |
Пример 3
На испытание поставлено N 0 =400 изделий. За время t= 3000 ч отказало n(t) =200 изделий, за интервал ∆t = 100 ч отказало n(∆t)= 100 изделий. Требуется определить вероятность безотказной работы за 3000 ч, вероятность безотказной работы за 3100 ч, вероятность безотказной работы за 3050 ч, частоту отказов f (3050), интенсивность отказа λ (3050).
Временной график
 ]
]
 | |||
 | |||

| Дано: N = 400 шт. t = 3000 ч n = 200 шт. ∆t = 100 ч n(∆t) = 100 шт. Найти: Р (3000), Р (3050), Р (3100), f (3050), λ (3050). | Решение:
Вероятность безотказной работы будем искать по формуле:
P(t) =  ;
Р (3100) = ;
Р (3100) = 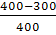 = 0,25;
Для t =3000 ч (начало интервала)
Р (3000) = = 0,25;
Для t =3000 ч (начало интервала)
Р (3000) = 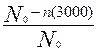 = =  = 0,5;
Для t =3100 ч (конец интервала)
Р (3100) = = 0,5;
Для t =3100 ч (конец интервала)
Р (3100) =  = = 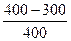 = 0,25;
Среднее время исправно работающих изделий в интервале ∆t: = 0,25;
Среднее время исправно работающих изделий в интервале ∆t:
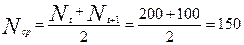 .
Число отказавших за время t= 3050 ч
n (3050) = N 0 - N ср= 400 – 150 =250, тогда
Р (3050) = .
Число отказавших за время t= 3050 ч
n (3050) = N 0 - N ср= 400 – 150 =250, тогда
Р (3050) = 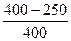 = 0,375;
Определяется частота отказа:
f (3050) = = 0,375;
Определяется частота отказа:
f (3050) = 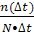 ;
f (3050) = ;
f (3050) = 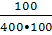 = 0,0025 = 2,5٠10 -2; ч -1.
Так же определяется частота отказов за интервалы 3000 ч и 3100 ч, причем началом интервалов является t = 0.
f (3000) = = 0,0025 = 2,5٠10 -2; ч -1.
Так же определяется частота отказов за интервалы 3000 ч и 3100 ч, причем началом интервалов является t = 0.
f (3000) =  = 0,000167 = 1,67٠10 -4 ч -1;
f (3100) = = 0,000167 = 1,67٠10 -4 ч -1;
f (3100) = 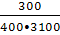 = 0,00024 = 2,4٠10 -4 ч -1.
Определяется интенсивность отказов:
а) в интервале ∆t =3050 ч
λ (3050) = = 0,00024 = 2,4٠10 -4 ч -1.
Определяется интенсивность отказов:
а) в интервале ∆t =3050 ч
λ (3050) = 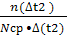 ;
λ (3050) = ;
λ (3050) = 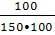 = 0,0067 ч -1;
б) в интервале ∆t =3000 ч
Nср (3000) = 400 – 100 = 300 шт;
λ (3000) = = 0,0067 ч -1;
б) в интервале ∆t =3000 ч
Nср (3000) = 400 – 100 = 300 шт;
λ (3000) = 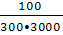 = 0,000222 =2,22٠10 -4 ч -1;
в) в интервале ∆t =3100 ч
Nср (3100) = 400 – 150 = 250 шт;
λ (3100) = = 0,000222 =2,22٠10 -4 ч -1;
в) в интервале ∆t =3100 ч
Nср (3100) = 400 – 150 = 250 шт;
λ (3100) = 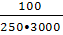 = 0,00039 ч -1. = 0,00039 ч -1.
|
Пример 5
В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь периодов зарегистрировано n= 15 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1233 ч. Определить среднюю наработку на отказ t ср.
| Дано: n = 15 t1 = 258 ч t2 = 1233 ч | Решение:
Наработка за указанный период составила
∆t = t1 – t2 = 1233 – 258 = 975 ч;
Наработка на отказ по статистическим данным определяется по формуле:
t ср = 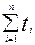 / n,
где t i - время исправной работы между
(i -1) и i отказами, n – число отказов за некоторое время t.
Приняв / n,
где t i - время исправной работы между
(i -1) и i отказами, n – число отказов за некоторое время t.
Приняв 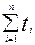 = 975 ч, можно определить среднюю наработку на отказ
t ср = = 975 ч, можно определить среднюю наработку на отказ
t ср = 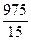 = 65 ч. = 65 ч.
|
| Найти: t ср |
Пример 6
Производилось наблюдение за работой трех однотипных объектов. За период наблюдения было зафиксировано по первому объекту 6 отказов, по второму - 11 отказов, третьему - 8 отказов. Наработка первого объекта t1 = 6 181 ч, второго
t2 = 329 ч, третьего t3 = 245 ч. Определить наработку объектов на отказ.
| Дано: N = 3 n1 = 6 n2 = 11 n3 = 8 t1 = 181 ч t2 = 329 ч t3 = 245 ч | Решение:
1 вариант решени:.
t ср= 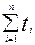 / ni;
t ср =; / ni;
t ср =; 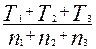 t ср =
t ср = 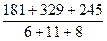 = 30,2 ч
2 вариант решения:
t ср 1 = = 30,2 ч
2 вариант решения:
t ср 1 = 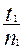 , t ср 2 = , t ср 2 = 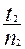 , t ср 3 = , t ср 3 = 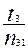 ;
t ср 1 = ;
t ср 1 = 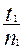 , t ср 2 = , t ср 2 = 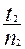 , t ср 3 = , t ср 3 = 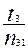 ;
t ср 1 = ;
t ср 1 = 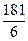 = 30,2 ч;
t ср 2 = = 30,2 ч;
t ср 2 = 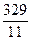 = 29,9 ч;
t ср 3 = = 29,9 ч;
t ср 3 = 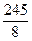 = 3,6 ч;
t ср= (30,2 + 29,9 + 30,6)/3 = 30,2 ч. = 3,6 ч;
t ср= (30,2 + 29,9 + 30,6)/3 = 30,2 ч.
|
| Найти: t ср |
Как видно, у задачи есть два способа решения. Первый основан на использовании общей формулы вычисления средней наработки. Во втором варианте решения применяется более детальный способ. Сначала находится средняя наработка для каждого элемента, а среднее значение этих чисел и есть то, что определяется.
Пример 7
Система состоит из 5 приборов, причем отказ любого одного из них ведет к отказу системы. Известно, что первый отказал 34 раза в течение 952 ч работы, второй – 24 раза в течение 960 ч работы, а остальные приборы в течение 210 ч работы отказала 4, 6 и 5 раз соответственно. Требуется определить наработку на отказ системы в целом, если справедлив экспоненциальный закон надежности для каждого из пяти приборов.
| Дано: N = 5 n1 = 34 n2 = 24 n3 = 4 n4 = 6 n5 = 5 t1 = 952 ч t2 = 960 ч t3-5 = 210 ч | Решение:
Используются следующие соотношения:
λс =  ;
tcp = ;
tcp = 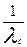 ;
Определяется интенсивность отказов для каждого прибора
(N = 1):
λi = ;
Определяется интенсивность отказов для каждого прибора
(N = 1):
λi = 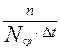 ,
где Nср- среднее число исправно работающих изделий в интервале ∆ t.
λ1 = ,
где Nср- среднее число исправно работающих изделий в интервале ∆ t.
λ1 = 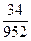 = 0,04 ч -1; λ2 = = 0,04 ч -1; λ2 = 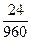 = 0,025 ч -1; λ3 = = 0,025 ч -1; λ3 =  = 0,02 ч -1;
λ4 = = 0,02 ч -1;
λ4 =  = 0,03 ч -1; λ5 = = 0,03 ч -1; λ5 = 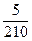 = 0,02 ч -1;
или = 0,02 ч -1;
или
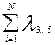 = = 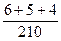 = 0,07 ч -1;
тогда интенсивность отказов системы будет
λс = = 0,07 ч -1;
тогда интенсивность отказов системы будет
λс =  = λ1 + λ2 + λ3-5 = 0,04 + 0,025 + 0,07 = 0,135 ч -1;
Средняя наработка на отказ системы равна
tcp = = λ1 + λ2 + λ3-5 = 0,04 + 0,025 + 0,07 = 0,135 ч -1;
Средняя наработка на отказ системы равна
tcp = 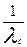 = = 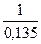 = 7,41 ч. = 7,41 ч.
|
| Найти: t ср |
Пример 8
За наблюдаемый период эксплуатации в аппаратуре было зафиксировано 8 отказов. Время восстановления составило: t1 = 12 мин, t2 = 23 мин, t3 = 15 мин, t4 = 9 мин,
t5 = 17 мин, t6 = 28 мин, t7 = 25 мин, t8 = 31 мин.
Требуется определить среднее время восстановления аппаратуры.
| Дано: n = 8 отказов t1 = 12 мин t2 = 23 мин t3 = 15 мин t4 = 9 мин t5 = 17 мин t6 = 28 мин t7 = 25 мин t8 = 31 мин | Решение:
tср в = 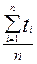 ;
tср в = ;
tср в = 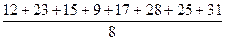 = 20 мин. = 20 мин.
|
| Найти: tср в |
Пример 9
Аппаратура имела среднюю наработку на отказ tcp = 65 ч и среднее время восстановления tв = 1,25 ч. Требуется определить коэффициент готовности Кг.
| Дано: tcp = 65 ч tв = 1,25 ч | Решение:
Кг = 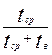 ;
Кг = ;
Кг = 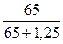 = 0,98. = 0,98.
|
| Найти: Кг |
Пример 10
Пусть время работы элемента до отказа подчинено экспоненциальному закону λ = 2,5 ٠10-5 ч -1. Требуется определить вероятность безотказной работы P(t), частоту отказов f(t) и среднюю наработку на отказ tср, если t = 500, 1000, 2000 ч.
| Дано: λ = 2,5 ٠10 -5 ч -1 t1 = 500 ч t2 = 1000 ч t3 = 2000 ч | Решение:
Р(t) = e-λt;
Р(t1) = e-2.5٠0.00001•500 = 0,98;
Р(t2) = e-2.5٠0.00001•1000 = 0,97;
Р(t3) = e-2.5٠0.00001•2000 = 0,95;
f(t) = λ ٠ P(t);
f(t1) = 2,5٠10-5٠0.98 = 2.45٠10-5 ч -1;
f(t2) = λ ٠ P(t2) = 2,5٠10-5٠0.97 = 2.425٠10-5 ч -1;
f(t3) = λ ٠ P(t3) = 2,5٠10-5٠0.95 = 2.375٠10-5 ч -1;
tср = 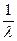 ;
tср = ;
tср = 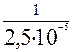 = 4٠10 4 ч. = 4٠10 4 ч.
|
| Найти: P(t), f(t), tср |
Пример 11
Время работы изделия до отказа подчиняется закону Рэлея. Требуется определить количественные характеристики: P(t), f(t), λ(t), tср, при t1 = 500 ч, t2 = 1000 ч, t3 = 2000 ч. Если параметр распределения σ = 1000 ч.
| Дано: t1 = 500 ч t2 = 1000 ч t3 = 2000 ч σ = 1000 ч | Решение:
f(t) = 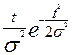 ;
f (500) = ;
f (500) = 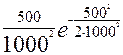 = 4٠10-4 ч -1;
f (1000) = = 4٠10-4 ч -1;
f (1000) = 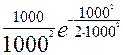 = 6,1٠10-4 ч -1;
f (2000) = = 6,1٠10-4 ч -1;
f (2000) = 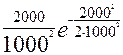 = 2,7٠10-4 ч -1;
Р(t) = = 2,7٠10-4 ч -1;
Р(t) = 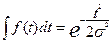 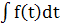 = = 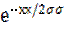 ;
Р (500) = ;
Р (500) = 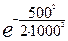 = 0,88;
Р (1000) = = 0,88;
Р (1000) =  = 0,61;
Р (2000) = = 0,61;
Р (2000) = 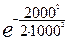 = 0,14
λ(t) = = 0,14
λ(t) = 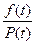 ;
λ (500) = ;
λ (500) = 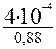 = 4,5•10-4 ч -1;
λ (1000) = = 4,5•10-4 ч -1;
λ (1000) = 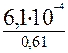 = 10٠10-4 ч -1;
λ (2000) = = 10٠10-4 ч -1;
λ (2000) = 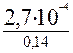 = 19,3٠10-4 ч -1;
tср = = 19,3٠10-4 ч -1;
tср = 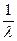 ;
tср (500) = ;
tср (500) =  = 2,2٠103 ч;
tср (1000) = = 2,2٠103 ч;
tср (1000) = 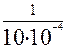 = 103 ч;
tср (2000) = = 103 ч;
tср (2000) = 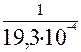 = 0,05٠103 ч. = 0,05٠103 ч.
|
| Найти: P(t), f(t), λ(t), tср, |
Пример 12.
Время безотказной работы гироскопического устройства с шарикоподшипниками в осях ротора гироскопа подчиняется закону Вейбулла - Гнеденко с параметрами k = 1,5, λо = 10-4 ч -1, а время его работы t = 100 ч. Требуется вычислить количественные характеристики надежности такого устройства.
Решение. 
k = 1,5 Используются формулы закона Вейбулла - Гнеденко для
λо = 10-4 ч -1. определения количественных характеристик:
t = 100 ч. Определяется вероятность безотказной работы:
Р(t) = 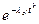 .
.
 Р (100) =
Р (100) = 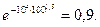
Найти: Р(t), f(t) Частота отказов определяется по формуле:
λ(t), tср f(t) = 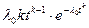
Тогда
f( 100) = 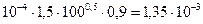 ч -1
ч -1
Интенсивность отказов определяется по формуле:
λ(t) = 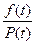 .
.
λ (100) = ч -1 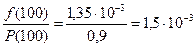
Вычисляется средняя наработка до первого отказа:
tср = 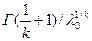
Сначала вычисляют значение гамма-функции, воспользовавшись справочными данными ([54], таблица П.7.18). В данном случае х = (1/ k)+1 = (1/1,5)+1 = 1,67.
Значения гамма-функции
| х | Г (х) |
| 1,67 | 0,90330 |
Полученные данные подставляются в формулу [54]:
tср = 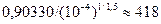 ч
ч
Пример 13.
Известно, что интенсивность отказов λ = 0,02 ч -1, а среднее время восстановления tВ = 10 ч. Требуется вычислить коэффициент готовности изделия.
Решение.
 tВ = 10 ч. Коэффициент готовности изделия определяется по
tВ = 10 ч. Коэффициент готовности изделия определяется по
λ = 0,02 ч -1. формуле:
 КГ =
КГ = 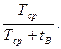
Найти: КГ Средняя наработка до первого отказа равна:
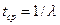 ,
,
Тогда:
КГ = 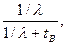
КГ = 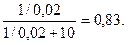
Пример 14.
Система состоит из 12600 элементов, средняя интенсивность отказов которых λ ср = 0,32٠10-6 ч -1.
Необходимо определить вероятность безотказной работы в течение t = 50 ч.
Решение.
N = 12600 Интенсивность отказов системы определим по фор-
λ с р = 0,32*10-6 ч -1. муле:
t = 50 ч. λ с = λ ср N =0,32٠10-6٠12600=4,032٠10-3 ч -1
 Вероятность безотказной работы по экспоненциальному
Вероятность безотказной работы по экспоненциальному
Найти: P(t) закону равна:
 P (50) = е -λсt =
P (50) = е -λсt = 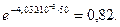
Пример 15.
Система состоит из N = 5 блоков. Надежность блоков характеризуется вероятностью безотказной работы в течение времени t, которая равна: p1(t) = 0,98; p2(t) = 0,99; p3(t) = 0,97; p4(t) = 0,985; p5(t) = 0,975.
Требуется определить вероятность безотказной работы системы.
 Решение.
Решение.
N = 5 Воспользуемся формулой для определения безотказной ра-
p1(t) = 0,98 боты системы:
p2(t) = 0,99 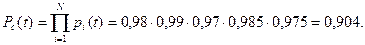
p3(t) = 0,97 Данные вероятности близки к единице, поэтому вычислить
p4(t) = 0,985 Рс(t) удобно, использовав приближенную формулу.
p5(t) = 0,975 В нашем случае q1 =0,02; q2 =0,01; q3 =0,03; q4 =0,015;
 q5 =0,025. Тогда:
q5 =0,025. Тогда:
Найти: Рс(t)
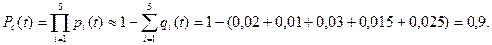
Пример 16
Система состоит из трех устройств. Интенсивность отказов электронного устройства равна λ1 = 0,16٠10-3 ч -1 = const. Интенсивности отказов двух электромеханических устройств линейно зависят от времени и определяются следующими формулами: λ2 = 0,23٠10-4 t ч -1, λ3 = 0,06٠10-6 t 2,6 ч -1.
Нужно рассчитать вероятность безотказной работы изделия в течение 100 ч.
| Дано: N = 3 λ1 = 0,16٠10-3 ч -1 λ2 = 0,23٠10-4 t ч -1 λ3 = 0,06٠10-6 t2,6 ч -1 t = 100 ч | Решение:
На основании экспоненциального закона имеем
Р (t) =  ;
Так как λ ≠ const, то на основании формулы Рс (t) =
exp ( ;
Так как λ ≠ const, то на основании формулы Рс (t) =
exp (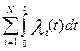 имеем
Рс (t) = exp {-[ имеем
Рс (t) = exp {-[ 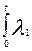 (t)dt + (t)dt + 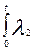 (t)dt + (t)dt + 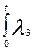 (t)dt]} = exp [ - ( (t)dt]} = exp [ - ( dt + dt + 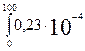 (t)dt + (t)dt +  (t)dt)];
Рс (100) = exp [ - (0,16٠10-3 ٠100 + 0,23٠10-4 ٠ (t)dt)];
Рс (100) = exp [ - (0,16٠10-3 ٠100 + 0,23٠10-4 ٠ 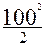 + 0,06٠10-6 ٠ + 0,06٠10-6 ٠ 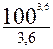 )] ≈ 0,33. )] ≈ 0,33.
|
| Найти: Р(t) |
Пример 17
Система состоит из трех блоков, средняя наработка до первого отказа которых равна Т1 =160 ч, Т2 = 320 ч, Т3 = 600 ч. Для блоков справедлив экспоненциальный закон надежности. Требуется определить среднюю наработку до первого отказа системы.
 Решение. Согласно экспоненциальному закону
Решение. Согласно экспоненциальному закону 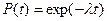
N = 3 Интенсивность отказов системы: 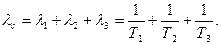
Т1 =160 ч Средняя наработка до первого отказа системы: 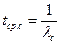
Т2 = 320 ч Значит: 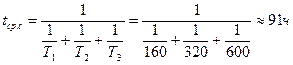
 Т3 = 600 ч
Т3 = 600 ч
Найти: tср с
Пример 18
Система состоит из двух устройств. Вероятности безотказной работы каждого из них в течение времени t = 100 ч равны: р1 (100) = 0,95; р2 (100) = 0,97. Справедлив экспоненциальный закон надежности. Необходимо найти среднюю наработку до первого отказа системы tср с.
| Дано: N = 2 t = 100 ч р1 (100) = 0,95 р2 (100) = 0,97 | Решение:
Определяется вероятность безотказной работы изделия: Рс (100) =
= р1 (100) р2 (100) = 0,95٠ 0,97 = 0,92;
Определяется интенсивность отказов изделия, воспользовавшись формулой
Рс (100) = 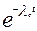 = = 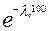 ;
0,92= ;
0,92= 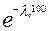 ;
λс ٠100 ≈ 0,083 ч -1,
тогда
tср с = ;
λс ٠100 ≈ 0,083 ч -1,
тогда
tср с = 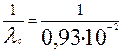 = 1200 ч = 1200 ч
|
| Найти: tср с |
Пример 19
Вероятность безотказной работы одного элемента в течение времени t равна p(t) = 0,9997. Требуется определить вероятность безотказной работы системы, состоящей из N = 100 таких же элементов.
Решение.
 1 вариант решения:
1 вариант решения:
p(t) = 0,9997 Если у всех элементов системы одинаковая надежность, то
N = 100 Pc(t) = pN(t) = (0,9997)100 = 0,9704.
 2 вариант решения:
2 вариант решения:
Pc -? Так как вероятность Pc(t) близка к единице, то можно
воспользоваться следующей формулой: Pc(t) = 1- Qc(t). Для одного элемента системы: q(t) = 1- p(t) = 1-0,9997 = 0,0003; то есть Qc(t) = N ٠ q(t) =100٠0,0003 = 0,03. Значит Pc(t) = 1-0,03 = 0,97.
Получается, что первый вариант решения более точен.
Пример 20
Вероятность безотказной работы системы в течении времени t равна Рс(t) = 0.95. система состоит из N = 120 равнонадежных элементов. Требуется определить вероятность безотказной работы элемента рi(t).
| Дано: Рс(t) = 0.95 N = 120 | Решение:
Очевидно, что вероятность безотказной работы элемента будет рi (t) = 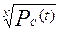 . Так как р (t) близка к единице, то вычисления р (t) удобно выполнять по формуле qс = 1 - рi(t) = 1 – 0,95 = 0,05.
Тогда
рi(t) = . Так как р (t) близка к единице, то вычисления р (t) удобно выполнять по формуле qс = 1 - рi(t) = 1 – 0,95 = 0,05.
Тогда
рi(t) = 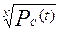 = 1 - = 1 - 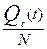 = 1 – = 1 – 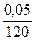 = 0.9996. = 0.9996.
|
| Найти: рi(t) |
Пример 21.В системе Nс = 2500 элементов и вероятность безотказной работы ее в течение одного часа Рс(1) = 98 %. Предполагается, что все элементы равнонадежны и интенсивность отказов элементов λ = 8,4٠10-6 ч -1. Требуется определить среднюю наработку до первого отказа системы t ср с.
Решение.
 Nс = 2500 Интенсивность отказов системы определим по формуле:
Nс = 2500 Интенсивность отказов системы определим по формуле:
Рс(1) = 98 % λс = N ٠ λ = 8,4٠10-6٠2500 = 0,021 ч -1,
λ = 8,4٠10-6 ч -1 средняя наработка до первого отказа системы равна:
 tср с = 1/ λс = 1/0,021 = 47,6 ч.
tср с = 1/ λс = 1/0,021 = 47,6 ч.
Найти: tср с
Пример 22.
Система состоит из пяти приборов, вероятности исправной работы которых в течение времени t = 100 часов равны: p1 (100) = 0,9996; p2 (100) = 0,9998; p3 (100) = 0,9996; p4 (100) = 0,999; p5 (100) = 0,9998. Требуется определить частоту отказов системы в момент времени t = 100 часов.
Предполагается, что отказы приборов независимы и для них справедлив экспоненциальный закон надежности.
Решение.
t = 100 ч По условиям задачи отказы приборов независимы,
p1 (100) = 0,9996 поэтому вероятность безотказной работы системы равна
p2 (100) = 0,9998 произведению вероятностей безотказной работы прибо-
p3 (100) = 0,9996 ров. Тогда по формуле для высоконадежных систем име-
p4 (100) = 0,999 ем: p1(t) p2(t) p3(t)… pN(t) 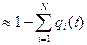
p5( 100) = 0,9998 Pc (100) 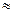 1-
1- 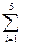 Qi (100) = 1-(0,004+0,0002+0,0004+
Qi (100) = 1-(0,004+0,0002+0,0004+
 +0,001+0,0002) = 0,9978.
+0,001+0,0002) = 0,9978.
Найти: fс
Так как вероятность безотказной работы системы близка к единице, то в соответствии с формулой
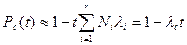
интенсивность отказов можно вычислить следующим образом:
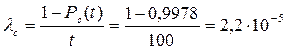 ч -1,
ч -1,
тогда частоту отказов определим в соответствии с формулой:
ас(t) 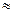 λс(1- λсt) = 2,2٠10-5(1-2,2٠10-5٠100) = 2,195٠10-5 ч -1.
λс(1- λсt) = 2,2٠10-5(1-2,2٠10-5٠100) = 2,195٠10-5 ч -1.
Пример 23
Изделие состоит из 1 маломощного низкочастотного германиевого транзистора, 4 плоскостных кремниевых выпрямителей, 1 керамического конденсатора, 1 резистора типа МЛТ, 10 силовых трансформаторов, 3 накальных трансформаторов, 1 дросселя и 9 катушек индуктивности. Необходимо найти вероятность безотказной работы изделия в течение t =200 часов и среднюю наработку до первого отказа.
Решение.
N1 =1,
N2 =4
N3 =1
N4 =1
N5 =10
N6 =3
N7 =1
N8 =9
t =200 ч

Найти: Рс (200), tср с
Для решения данной задачи составляется и заполняется таблица 14.1, после вычисления величин интенсивности отказов изделия.
интенсивность отакзов элементов
Таблица 14.1
| Наименование и тип элемента | Количество элементов Ni | Интенсивность отказов, 10-5 ч -1 | Ni λi 10-5 ч -1 |
| Маломощный низкочастотный германиевый транзистор | |||
| Плоскостной кремниевый выпрямитель | 0,5 | ||
| Керамический конденсатор | |||
| Резистор типа МЛТ | 0,3 | 0,3 | |
| Силовой трансформатор | 0,22 | 2,2 | |
| Накальный трансформатор | 1,5 | 4,5 | |
| Дроссель | 2,3 | 2,3 | |
| Катушка индуктивности | 1,8 | 16,2 |
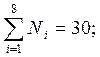
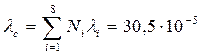 ч -1
ч -1
По данным таблицы и по формуле для экспоненциального закона находим вероятность безотказной работы изделия в течение t = 200 ч и среднюю наработку до первого отказа:
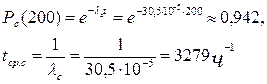
Date: 2015-07-17; view: 106455; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |