
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Нормальный закон распределения наработки до отказа
Нормальное распределение вероятности безотказной работы описывает схему длительного «естественного» старения (постепенные отказы). В этом случае отказы являются следствием накопления повреждений:
– при постоянной скорости износа;
– однородном начальном качестве объектов.
При таких начальных условиях большая часть отказов наблюдается в течение конечного периода работы объекта.
Нормальное распределение или распределение Гаусса является наиболее универсальным, удобным и широко применимым.
Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие примерно равнозначные факторы.
Нормальному распределению подчиняется наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий, размеры, ошибки измерения деталей и т. д.
Плотность распределения отказов описывается формулой:
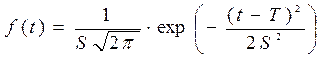 . (4.9)
. (4.9)
Распределение имеет два независимых параметра: математическое ожидание mt и среднее квадратическое отклонение S.
 , (4.10)
, (4.10)
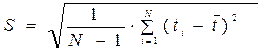 . (4.11)
. (4.11)
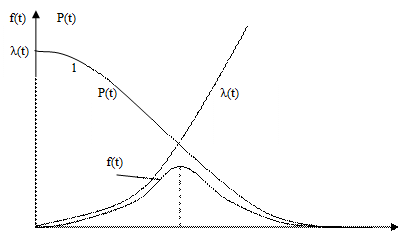
Графики изменения показателей безотказности при нормальном распределении приведены на рисунке 4.5.
Выясним смысл параметров Т и S нормального распределения. Из графика f (t) видно, что Т является центром симметрии распределения, поскольку при изменении знака разности (t - Т) выражение (4.9) не меняется. При t = Т функция f (t) достигает своего максимума:
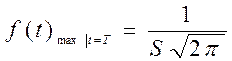 . (4.12)
. (4.12)
 | |||
 |
Рис.4.5 Графики функций показателей безотказности при нормальном распределении.
Параметр S характеризует форму кривой f(t), то есть рассеивание случайной величины T. Кривая плотности распределения f (t) тем выше и острее, чем меньше S. Она начинается от t = – ∞ и распространяется до t = ∞. Это не является существенным недостатком, если T ≥ 3 S, так как площадь, очерченная уходящими в бесконечность ветвями кривой плотности, очень мала. Так, вероятность отказа за период времени до Т = – 3 S составляет всего 0,135 % и обычно не учитывается в расчетах. Наибольшая ордината кривой плотности распределения равна 0,399 /S (рис 4.6)
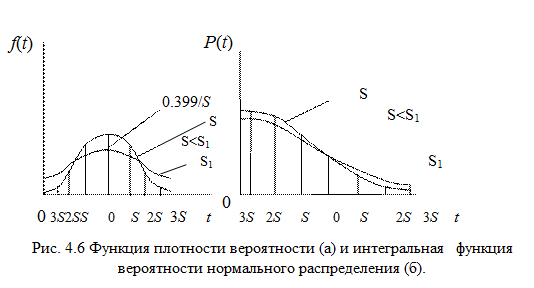
Вероятность отказа при таком распределении определяется интегральной функцией
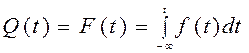 , (4.13)
, (4.13)
вероятность безотказной работы
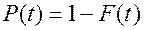 , (4.14)
, (4.14)
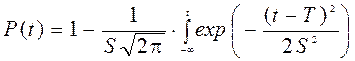 . (4.15)
. (4.15)
Вычисление интегралов заменяют использованием таблиц значений P (t) в зависимости от квантили нормированного нормального распределения (таблица 4.3):
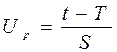 . (4.16)
. (4.16)
Помимо прямой задачи, то есть оценки вероятности безотказной работы за данную наработку, зачастую требует решения обратное определение наработки, соответствующей заданной вероятности безотказной работы.
Значение этой наработки определяют также с помощью квантили:
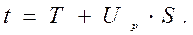 (4.17)
(4.17)
Нормальное распределение
Таблица 4.3
| Квантиль U p | Вероятность безотказной работы P (t) | Квантиль U p | Вероятность безотказной работы P (t) |
| 0,0 | 0,5000 | -1,282 | 0,9000 |
| -0,1 | 0,5398 | -1,400 | 0,9192 |
| -0,2 | 0,5793 | -1,600 | 0,9452 |
| -0,3 | 0,6179 | -1,800 | 0,9641 |
| -0,4 | 0,6552 | -2,000 | 0,9772 |
| -0,5 | 0,6915 | -2,200 | 0,9861 |
| -0,6 | 0,7257 | -2,236 | 0,9900 |
| -0,7 | 0,7580 | -2,500 | 0,9938 |
| -0,8 | 0,7881 | -3,090 | 0,9990 |
| -0,9 | 0,8159 | -3,500 | 0,9998 |
| -1,0 | 0,8413 | -3,719 | 0,9999 |
Применение нормального закона ограничено, если мала вероятность отрицательных значений времени безотказной работы, заданная в виде:
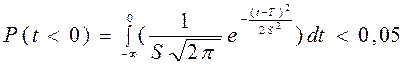 . (4.18)
. (4.18)
Если вероятность отрицательных значений времени безотказной работы оказывается достаточно большой величиной, то нормальное распределение для расчетов надёжности использовать нельзя. В этом случае переходят к логарифмически нормальному распределению вероятности безотказной работы.
При большем разбросе значений случайной величины T область возможных значений ограничивается слева (0, ∞) и используется усеченное нормальное распределение.
Все рассмотренные далее законы распределения наработки до отказа используются на практике для описания надёжности «стареющих» объектов, подверженных отказам вследствие износа.
Date: 2015-07-17; view: 2083; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |