
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Усеченное нормальное распределение
Усеченным нормальным распределением называется распределение, получаемое из классического нормального при ограничении интервала возможных значений наработки до отказа.
Известно, что корректность использования классического нормального распределения наработки достигается при Т ≥ 3 S.
При малых значениях Т и большом S может возникать ситуация, когда функция f (t) «покрывает» своей левой ветвью область отрицательных наработок (рисунок 4.7).
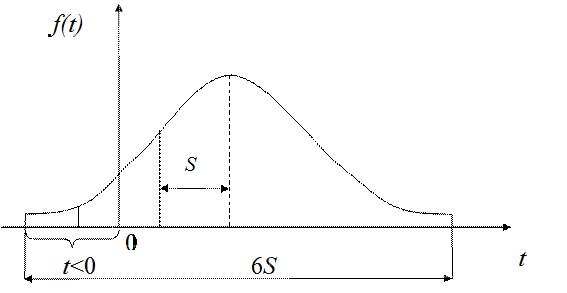
Рис. 4.7 Функция плотности вероятности усеченного нормального распределения
Таким образом, нормальное распределение, являясь общим случаем распределения случайной величины в диапазоне (– ∞; +∞), лишь в частности (при определенных условиях) может быть использовано для моделей надёжности.
В общем случае усечение может быть:
левым – (0; +∞);
двусторонним – (t 1, t 2).
Для рассмотрения количественных характеристик надёжности при усеченном нормальном распределении вводится нормирующий множитель, чтобы сохранить условие нормирования плотности вероятности:
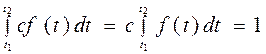 , (4.19)
, (4.19)
где
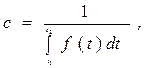
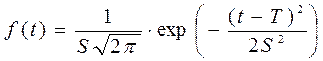 , (4.20)
, (4.20)

откуда
переходя от случайной величины Т = { t } к величине X = { x }:
x 2 = (t 2 –Т) /S, x 1 = (t 1 – Т) /S,
|
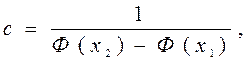 получают
получают 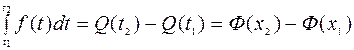 ,
,
откуда:
где Ф (х) – интеграл Лапласа

Усеченный нормальный закон распределения применяется для описания постепенных отказов объектов, что характерно для «стареющих» объектов.
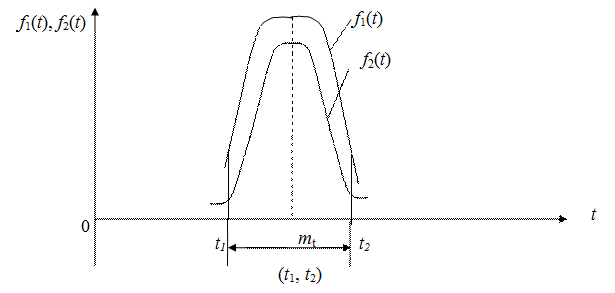
Поскольку [ Ф (x 2) –Ф (x 1)] < 1, то c > 1, поэтому f 1(t) > f 2(t). Здесь f 1(t) – функция плотности распределения отказов для нормального закона распределения, f 2(t) – функция плотности распределения отказов для усеченного нормального закона распределения. Кривая f 1(t) выше, чем f 2(t), так как площади под кривыми f 1(t) и f 2(t) одинаковы и равны 1 (рис. 4.8):
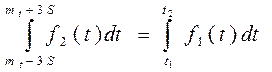
(с погрешностью ≤ 1%)



 Контрольные вопросы
Контрольные вопросы
1 Почему распределение Гаусса называется нормальным?
2 Поясните на изменении кривой плотности распределения отказов влияние параметров распределения: математического ожидания и дисперсии.
3 При каких условиях правильно использовать классическое нормальное распределение, а при каких – усечённое нормальное распределение?
Date: 2015-07-17; view: 5123; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |