Логарифмически нормальное распределение

При логарифмически нормальном распределении нормально распределенным является логарифм (lg t) случайной величины Т, а не сама эта величина.

Это распределение обеспечивает более точное, чем нормальное распределение, описание наработки до отказа тех объектов, у которых отказ возникает вследствие усталости, например, подшипников качения, электронных ламп и пр.

Оно используется при обработке опытных данных об усталостной долговечности металлов, времени безотказной работы некоторых объектов.

Логарифмически нормальное распределение позволяет описывать течение времени безотказной работы объектов, имеющих свойство «упрочняться» по ходу времени эксплуатации. «Упрочнение» сказывается в постепенном уменьшении скорости износа.

Плотность распределения выражается зависимостью:

. (4.23)

Параметры m и S по результатам N испытаний принимаются:

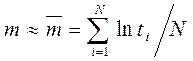, (4.24)

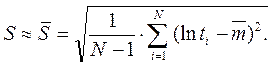(4.25)

Вероятность безотказной работы можно определить по таблице нормального распределения (см. табл. 4.3) в зависимости от значения квантили:

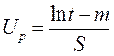. (4.26)

Математическое ожидание наработки до отказа:

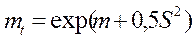. (4.27)

Среднее квадратическое отклонение

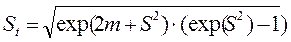. (4.28)

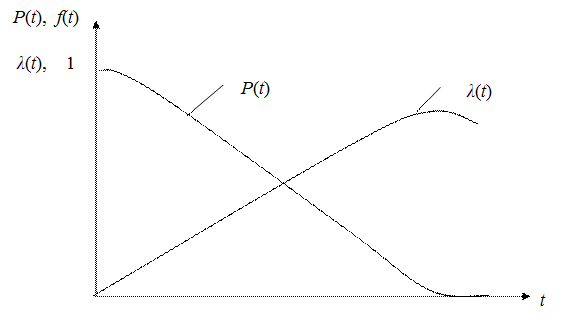
Графики изменения показателей надежности при логарифмически нормальном распределении приведены на рисунке 4.9.