Средняя квадратическая ошибка простой

Арифметической средины

Дан ряд результатов равноточных измерений одной величины

x _1, x ₂ ,..., x.

Представим формулу для вычисления простой арифметической средины в виде

` x = (1.56)

Согласно (1.47) будем иметь

(1.57)

где m ₁ = m ₂ =... = m _n = m. Следовательно, равенство (1.57) примет следующий вид

и окончательно запишем

(1.58)

Итак, средняя квадратическая ошибка простой арифметической средины в корень квадратный раз из числа измерений меньше средней квадратической ошибки одного измерения.

Формула Бесселя

Выполнив n повторных измерений одной и той же величины, вычислим отклонения результатов этих измерений от арифметической средины

Получим формулу для оценки точности результата измерения через отклонения от арифметической средины, но предварительно рассмотрим свойства отклонений v_i [ 2 ].

Первое свойство. Алгебраическая сумма отклонений результатов равноточных измерений одной и той же величины от простой арифметической средины равна нулю при любом числе измерений.
Возьмем ряд отклонений от арифметической средины

(1.59)

Суммируя левую и правую части равенства (1.59), получим

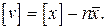
Полученное равенство разделим на n

. (1.60)

Поскольку правая часть равенства (1.60) равна нулю, то и [n] = 0.

Второе свойство. Сумма квадратов отклонений результатов равноточных измерений от простой арифметической средины меньше суммы квадратов отклонений этих же результатов от любой другой величины, не равной простой арифметической средины, т.е. если x¢ ¹ ` x, то

[ vv ] < [ ee ], (1.61)

где

v_i = x_i - ` x, e_i = x_i - x¢.

Докажем второе свойство отклонений v_i алгебраическим путем. Вычтем v_i из e_i по частям: из правого равенства левое

e_i - v_i = x_i - x¢ - x_i + ` x = ` x - x¢ = c. (1.62)

Для n числа наблюдений получим ряд отклонений e_i

e ₁ = v ₁ + c,

e ₂ = v ₂ + c, (1.63)

.........

e_n = v_n + c.

Возведем в квадрат равенства (1.63) и, суммируя левую и правую части, получим

[ ee ] = [ vv ] + nc ² + 2 c [ v ]. (1.64)

Но член 2 c [ v ] = 0 по первому свойству отклонений v_i, тогда

[ ee ] = [ vv ] + nc ². (1.65)

Из формулы (1.65) следует, что

[ ee ] > [ vv ]

на положительное число nc ², вне зависимости от того, x¢ больше` x, или меньше. Таким образом, при x¢ ¹ x

[ vv ] < [ ee ], (1.66)

что и требовалось доказать.

Для решения поставленной в начале данного параграфа задачи определим связь между истинными ошибками D _i и отклонениями v_i. Напишем

D _i = x_i - X; v_i = x_i - .

Cоставим разность

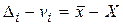. (1.67)

Возведем в квадрат равенства (1.67) и почленно просуммируем

. (1.68)

Согласно первому свойству отклонений имеем

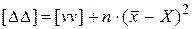. (1.69)

В равенстве (1.69) левая часть согласно формуле Гаусса равна

. (1.70)

Разность данного равенства соответствует средней квадратической ошибке значения среднего арифметического из результатов измерений, т.е. равна М. Тогда с учетом вышеизложенного получим вместо равенства (1.69) следующее

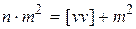
или

.

Откуда средняя квадратическая ошибка результата измерения составит

. (1.71)

Средняя квадратическая ошибка вычисления ошибки согласно формуле (1.71) равна

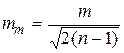. (1.72)

Date: 2016-07-25; view: 542; Нарушение авторских прав