Неопределенный интеграл, методы интегрирования

1. Понятия первообразной и неопределенного интеграла.

Функция называется первообразной для функции , если .

Множество всех первообразных функции задается формулой F(x)+C, где С – произвольное число, и называется неопределенным интегралом от функции :

.

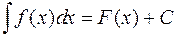2. Свойства неопределенного интеграла.

;

,

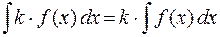где k – постоянная, отличная от нуля.

3. Таблица интегралов.

1. 8.

2. 9.

3. 10.

4. 11.

5. 12.

6. 13.

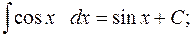7. 14.

15.

Примечание. Формулы верны, когда переменная х является независимой переменной, а также когда х является функцией другой переменной: х = х(t).

4. Основные методы интегрирования.

Идея всех методов интегрирования заключается в приведении искомого интеграла к табличному интегралу или сумме табличных интегралов.

1) Непосредственное интегрирование.

Интеграл приводится к табличному виду путем алгебраических или тригонометрических преобразований.

2) Замена переменной (интегрирование подстановкой).

Сведение интеграла к табличному виду осуществляется с помощью подстановки t = j(x). Тогда дифференциал dt равен

.

Рекомендации по введению новой переменной даны ниже в примерах.

3) Интегрирование по частям.

Интегрирование по частям производится по формуле

Этим методом интегрируются некоторые произведения, например, произведения степенной функции на логарифмическую, или на показательную, или на тригонометрическую, или на обратные тригонометрические функции.

Чтобы воспользоваться формулой, следует один множитель в подынтегральном выражении обозначить u, а другой множитель вместе с dx принять за dv.

Для того, чтобы интеграл в правой части был проще данного интеграла, надо правильно выбрать множители u и dv.

В интегралах, берущихся по частям, обычно логарифмическую и обратные тригонометрические функции принимают за u, а показательную или тригонометрические функции относят к dv.

5. Связь между интегрированием и дифференцированием.

Интегрирование – это операция, обратная дифференцированию. Если интеграл взят правильно, то производная от интеграла равна подынтегральной функции:

.

Задача. Найти неопределенные интегралы. Результаты проверить дифференцированием.

Решение. В контрольной работе интеграл под буквой а берется методом непосредственного интегрирования. При этом используются табличные интегралы от степенных функций:

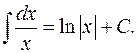
а)

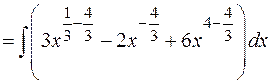
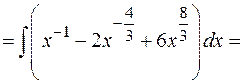
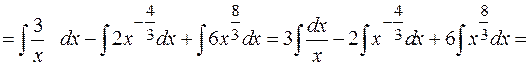
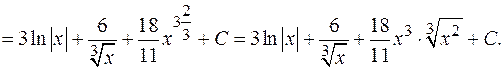
Проверка.

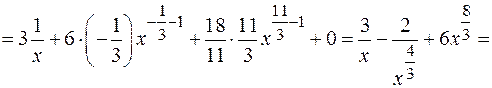
Получена подынтегральная функция, что и требовалось показать.

Интеграл б в контрольной работе берется методом замены переменной (подстановкой). Приведем ряд примеров.

б. 1)

За новую переменную возьмем аргумент подынтегральной функции 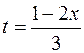и найдем dt по формуле:

Тогда

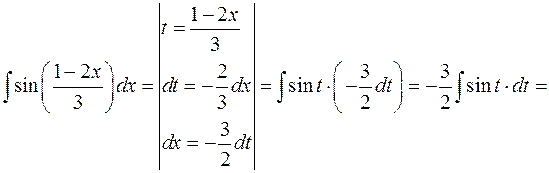
В последнем действии осуществлен переход к исходной переменной x с учетом, что .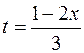

Проверка.

Что и требовалось показать.

б. 2) .

За новую переменную возьмем показатель степени .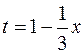

Тогда

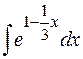
Проверка.

.

Получена подынтегральная функция.

б. 3) .

За новую переменную возьмем подкоренное выражение .

Проверка.

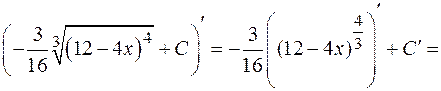
Что и требовалось показать.

б. 4) .

За новую переменную возьмем функцию, стоящую в основании степени . Тогда

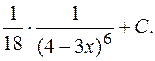
Проверка.

.

Получена подынтегральная функция.

Интеграл под буквой в в контрольной работе также берется методом замены переменной (подстановкой). Ознакомимся с примерами таких подстановок.

в. 1) .

За новую переменную удобно взять аргумент тригонометрической функции, если к тому же под интегралом присутствует производная этого аргумента (с точностью до постоянного множителя).

Проверка.

Что и требовалось показать.

в. 2) .

Здесь за новую переменную удобно принять показатель степени, учитывая, что под знаком интеграла присутствует производная этого показателя (с точностью до постоянного множителя).

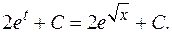
Проверка.

Что и требовалось показать.

в. 3) .

За новую переменную удобно взять подкоренное выражение, так как под интегралом присутствует также его производная (с точностью до постоянного множителя).

Проверка.

в. 4) .

За новую переменную берем функцию, стоящую в основании степени, так как подынтегральное выражение содержит производную этой функции (с точностью до постоянного множителя).

Проверка.

Что и требовалось показать.

в. 5) .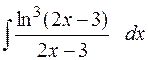

Здесь под интегралом содержится логарифмическая функция, удобно принять ее за новую переменную, учитывая, что под знаком интеграла присутствует производная этой функции (с точностью до постоянного множителя).

Проверка.

Что и требовалось показать.

В.6).

Часто удобно обозначать за новую переменную знаменатель дроби подынтегральной функции.

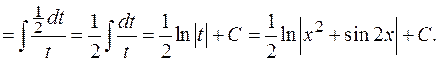
Проверка.

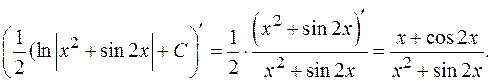
Что и требовалось показать.

Интеграл под буквой г берется методом интегрирования по частям:

.

г. 1) .

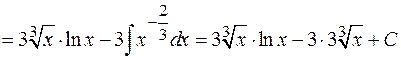
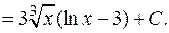
Проверка.

Что и требовалось показать.

г. 2) . ^*

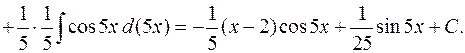
^*Решения задач г. 2 и г. 3 даны без проверки. Студент может выполнить её самостоятельно.

г. 3) .

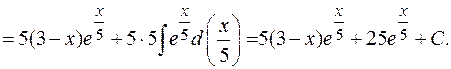
В пункте д предлагается взять интеграл от рациональной дроби.

Рациональная дробь – это отношение двух многочленов. Если степень многочлена в числителе строгоменьше степени многочлена в знаменателе, то дробь называется правильной. В противном случае дробь неправильная, она представляется в виде суммы некоторого многочлена и правильной рациональной дроби.

д) .

Под знаком интеграла стоит неправильная рациональная дробь, так как и в числителе и в знаменателе стоят многочлены первой степени (наивысшая степень ). Выделим целую часть с помощью следующих преобразований дроби:

Подставим полученное выражение под знак интеграла.

=

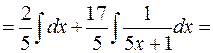
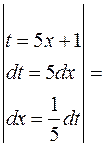
Проверка.

Получена подынтегральная функция.

Задачи 41–50