
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задач математического моделирования
Задачи ЛП образуют подмножество задач математического программирования. Отличительной особенностью задач ЛП является то, что целевая функция линейная и система ограничений также линейная. Возникновение и развитие ЛП связано с экономикой. Предположение о линейности экономических зависимостей несколько ограничивает возможности ЛП, однако простота и наглядность линейных моделей, с достаточной степенью точности описывающих экономические процессы, позволяет применять эти модели в различных видах экономической деятельности.
Большую роль в развитии ЛП сыграло создание в 1947 г. американским ученым Дж. Данцигом универсального метода решения задач, который получил название « симплекс- метод». Была осуществлена постановка и построена модель одной из центральных задач ЛП – транспортной задачи.
Основная задача ЛП формулируется так: дана линейная целевая функция
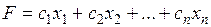 (1.1)
(1.1)
и задана система m>n линейных неравенств (ограничений)
 ,
,  (1.2)
(1.2)
 ,
, 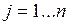
Необходимо найти максимум (минимум) целевой функции при выполнении условий (1.2).
Известно, что оптимальное решение задачи ЛП находится в одной из угловых вершин многогранной области допустимых решений. Угловых точек может быть много, если много ограничений. Количество угловых точек соответствует количеству базисных решений. Для каждого базисного решения однозначно определяется значение целевой функции. В связи с этим необходим такой переход от одного базисного решения к другому, в результате которого новое решение приносило бы в невырожденной задаче на максимум большее значение целевой функции, а в невырожденной задаче на минимум – меньшее. Такой процесс решения задачи реализует симплекс-метод, который называется методом последовательного улучшения плана. Процесс продолжается до получения оптимального плана или до установления факта отсутствия решений задачи.
Если задача ЛП вырожденная, то при переходе от одного базисного решения к другому значение целевой функции может не измениться. Переход от одного базисного решения к другому называется итерацией симплекс-метода или шагами.
Критерий разрешимости задачи ЛП: д ля того чтобы задача ЛП была разрешима, т.е. имела оптимальное решение, необходимо и достаточно, чтобы ограничения задачи были совместными (множество допустимых решений не пусто) и целевая функция была ограничена сверху при поиске максимума и снизу при поиске минимума.
Симплекс-метод может быть интерпретирован геометрически как движение по соседним угловым точкам многогранника решений. Точки называются соседними, если они расположены на одном ребре. Каждое неравенство системы (1.2) в задаче ЛП определяет в евклидовом n- мерном пространстве полупространство, состоящее из точек  , расположенных по «одну сторону» от плоскости и на самой этой плоскости. В результате система неравенств (1.2) образует некоторый выпуклый многогранник Ω, определяемый как область допустимых решений. Это означает, что любая точка, лежащая в этой области и на ее поверхности, удовлетворяет условиям ограничений задачи ЛП.
, расположенных по «одну сторону» от плоскости и на самой этой плоскости. В результате система неравенств (1.2) образует некоторый выпуклый многогранник Ω, определяемый как область допустимых решений. Это означает, что любая точка, лежащая в этой области и на ее поверхности, удовлетворяет условиям ограничений задачи ЛП.
Значение целевой функции (1.1) в точке  можно рассматривать как уклонение этой точки от плоскости
можно рассматривать как уклонение этой точки от плоскости
 , (1.3)
, (1.3)
понимая под уклонением данной точки от этой плоскости число, которое получим, подставив в левую часть уравнения (1.3) координаты этой точки  . Уклонение точки от плоскости (1.3) пропорционально расстоянию от точки до этой плоскости. Таким образом, геометрический смысл задачи ЛП заключается в отыскании в многограннике Ω точки, которая наиболее (наименее) уклонена от плоскости (1.3).
. Уклонение точки от плоскости (1.3) пропорционально расстоянию от точки до этой плоскости. Таким образом, геометрический смысл задачи ЛП заключается в отыскании в многограннике Ω точки, которая наиболее (наименее) уклонена от плоскости (1.3).
В случае двумерного пространства имеем картину, изображенную на рисунке 1.1. Здесь многогранником Ω является многоугольник, плоскостями - прямые, полупространствами- полуплоскости (см. рис 1). Ясно, что решением задачи ЛП будет какая-то вершина многогранника Ω, причем решение – единственное.

Рисунок 1.1 - Многогранник решений
Двумерные задачи линейного программирования решаются графически. Для случая N=3 можно рассмотреть трехмерное пространство и целевая функция примет оптимальное значение в одной из вершин многогранника. В общем виде, когда в задаче участвуют N - неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n- мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных больше трех, весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.
Симплекс - методявляется основным в линейном программирования. Решение задачи начинается с рассмотрения параметров одной из вершин многогранника. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней вершине, увеличивая значения функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. В результате переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.
Для использования симплекс-метода необходимо привести задачу к каноническому виду. Рассмотрим ее структуру.
Дана задача линейного программирования, которую необходимо записать в каноническом виде (рассмотрим случай, когда целевая функция  ):
):

при ограничениях
 ;
;
 ;
;
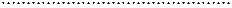
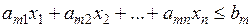
 ,
,  , …,
, …,  .
.
Преобразовав ограничения-неравенства в равенства, получим задачу в канонической форме записи:
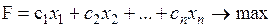
при ограничениях
 ;
;
 ;
;
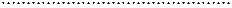 …….
…….
 ;
;
 ,
,  , …,
, …,  ,
,  , …,
, …,  .
.
Расчеты производят с помощью таблиц симплекс-метода. Симплекс - таблица состоит из четырех частей:
- корпуса таблицы;
- строки относительных оценок;
-столбца результата;
- значения целевой функции.
Содержание симплекс-таблицы представлено в таблице 1.1.
Таблица 1.1 – Структура симплекс-таблицы
| Небазисные переменные | ||||||
| Базисные переменные | x1 | x2 | x3 | … | xп | Столбец результата |
| x п+1 | а11 | а12 | а13 | … | а1п | b1 |
| x п+2 | а21 | а22 | а23 | … | а2п | b2 |
| xп+3 | а31 | а32 | а33 | … | а3п | b3 |
| … | … | … | … | … | … | |
| xп+т | ат1 | ат2 | ат3 | … | атп | bт |
| Δ1 | Δ2 | Δ3 | Δт | Δ | ||
| Строка относительных оценок | Значение целевой функции |
Строка относительных оценок рассчитывается по следующему правилу
 ;
;  ,
, 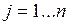 ,
,
т.е. величина строки относительных оценок j – ого столбца равна разности между скалярным произведением этого столбца матрицы А на вектор столбец, составленный из коэффициентов функции цели при базисных переменных и соответствующего коэффициента функции цели. Значение целевой функции рассчитывается следующим образом
 ;
;  .
.
Наличие в строке относительных оценок отрицательных значений свидетельствует о том, что данное решение (таблица) не является оптимальным и его можно улучшить. Улучшение достигается составлением новой таблицы с помощью процедуры повторяющихся расчетов - итераций. Итерации продолжаются до тех пор, пока не будет получено оптимальное решение, т. е. пока не исчезнут признаки неоптимальности. Итерация заключается в построение следующей симплекс - таблицы по определенным правилам.
Правила построения симплекс – таблицы:
1) в исходной таблице выбирают ключевой столбец. Ключевым считается тот столбец, которому соответствует минимальный отрицательный элемент в строке относительных оценок (если таких столбцов несколько, то выбираем любой из них);
2) в исходной таблице выбирается ключевая строка. Для ее выбора необходимо каждый элемент в столбце результата поделить на соответствующий ему положительный элемент ключевого столбца. Минимальное частное из полученных чисел соответствует ключевой строке (если минимальных частных несколько выбирают ту строку, которой соответствует наибольший элемент в ключевом столбце);
3) выбирается ключевой элемент, находящейся на пересечении ключевого столбца и ключевой строки;
4) строят макет следующей таблицы, в которой меняют местами базисная и небазисная переменная, соответствующие ключевому столбцу и ключевой строке;
5) ключевой элемент заменяется обратным к нему, относительно операции деления;
6) в ключевом столбце все элементы делят на ключевой элемент и знак меняется на противоположный; в ключевой строке все элементы делят на ключевой элемент;
7) все остальные элементы находят по определенному правилу:
 ,
,
где F - элемент новой таблицы;
Еаt - элемент предшествующей таблицы;
Eks - элемент ключевой строки;
Ekb - элемент ключевого столбца;
Ke - ключевой элемент.
Новую таблицу также исследуют на оптимальность. Если она такой не является, то рассчитывают следующую таблицу. Так продолжают до тех пор, пока в строке относительных элементов все числа станут неотрицательными величинами.
Date: 2016-07-18; view: 373; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |