
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Преобразования координат
Параллельный перенос. Гомотетия.
Симметрия. Аффинное преобразование.
Рассмотрим ряд преобразований, связанных с переходом из одной системы координат в другую. Здесь (х, у, z) и (х', у ', z ') - координаты произвольной точки Р соответственно в старой и новой системе координат.
Параллельный перенос. Передвинем систему координат X Y Z в трёхмерном пространстве так, чтобы оси OX, OY и OZ оставались параллельны самим себе, а начало координат О сместилось в точку О' (a, b, с). Получим новую систему координат X' Y' Z'.
Координаты точки Р в новой и старой системе координат связаны соотношениями:
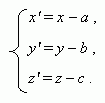
Гомотетия с центром О (a, b, c) и коэффициентом k  0:
0:
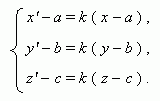
Симметрия относительно плоскости XOY:
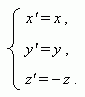
Аффинное преобразование:
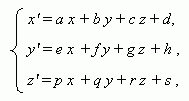

Плоскость
Общее уравнение плоскости. Нормальный вектор.
Уравнение плоскости в отрезках на осях.
Уравнение плоскости, проходящей через заданную
точку и перпендикулярной заданному вектору.
Параметрическое уравнение плоскости.
Условие параллельности плоскостей.
Условие перпендикулярности плоскостей.
Расстояние между двумя точками.
Расстояние от точки до плоскости.
Расстояние между параллельными плоскостями.
Угол между плоскостями.
Общее уравнение плоскости:
Ах + Ву + Сz + D = 0,
где А, B и C не равны нулю одновременно.
Коэффициенты А, B и C являются координатами нормального вектора плоскости (т.е. вектора, перпендикулярного плоскости).
При А  0, В
0, В  0, С
0, С  0 и D
0 и D  0 получаем уравнение плоскости в отрезках на осях:
0 получаем уравнение плоскости в отрезках на осях:
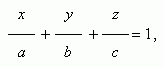
где a = – D / A, b = – D / B, c = – D / C. Эта плоскость проходит через точки (a, 0, 0), (0, b, 0) и (0, 0, с), т.е. отсекает на осях координат отрезки длиной a, b и c.
Уравнение плоскости, проходящей через точку (х 0, у 0, z 0) и перпендикулярной вектору (А, В, C):
А (х – х 0) + В (у – у 0) + С (z – z 0) = 0.
Параметрическое уравнение плоскости, проходящей через точку (х 0, у 0, z 0) и два неколлинеарных вектора (a 1, b 1, c 1) и(a 2, b 2, c 2), заданных в прямоугольной декартовой системе координат:

Условие параллельности плоскостей Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:
AF – BE = BG – CF = AG – CE = 0.
Условие перпендикулярности плоскостей Ах+ Ву+ Сz+ D = 0 и Eх+Fу+ Gz+ H = 0:
АE+ ВF+ СG = 0.
Расстояние между двумя точками (х 1, у 1, z 1) и(x 2, y 2, z 2):

Расстояние от точки (х 0, у 0, z 0) до плоскости Ах + Ву + Сz + D = 0:
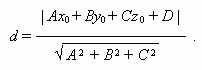
Расстояние между параллельными плоскостями Aх + By + Cz + D = 0 и Aх + By + Cz + Е = 0
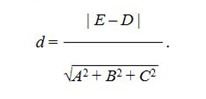
Угол  между плоскостями Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:
между плоскостями Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:
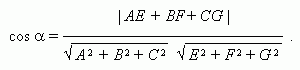
Прямая
Уравнение прямой, проходящей через две различные точки.
Параметрическое уравнение прямой. Уравнение линии
пересечения плоскостей. Условие параллельности прямых.
Условие перпендикулярности прямых. Угол между прямыми.
Угол между прямой и плоскостью.
Уравнение прямой, проходящей через две различные точки (х 1, у 1, z 1) и (х 2, у 2, z 2):

Параметрическое уравнение прямой, проходящей через точку (х 0, у 0, z 0) и параллельной направляющему вектору прямой (a, b, с):
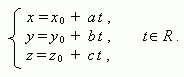
Пусть заданы две плоскости Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0, причём их нормальные векторы неколлинеарны, тогда система уравнений
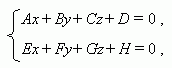
описывает прямую – линию пересечения этих плоскостей.
Пусть (a, b, с) и (p, q, r) – направляющие векторы двух прямых, тогда имеем условие параллельности прямых:
aq – bp = br – cq = ar – cp = 0,
условие перпендикулярности прямых:
ap + bq + cr = 0,
угол  между прямыми:
между прямыми:
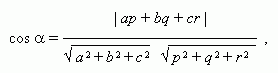
угол  между прямой и плоскостью:
между прямой и плоскостью:
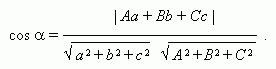
Сфера
Уравнение сферы радиуса R с центром в точке (a, b, с)имеет вид:
(x – a) 2 + (y – b) 2 + (z – c) 2 = R 2.
Date: 2016-11-17; view: 369; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |